树及二叉树笔记

数据结构之树（Tree）

笔者本来是准备看JDK HashMap源码的，结果深陷红黑树中不能自拔，特撰此篇以加深对树的理解

定义

首先来看树的定义：

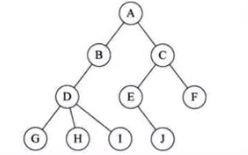
树（Tree）是n（n≥0）个节点的有限集。n = 0 时称为空树。在任意一棵非空树中：1、有且仅有一个特定的节点称为根（Root）的节点。2、当n > 1时，其余节点可分为m（m > 0）个互不相交的有限集T1、T2、T3、……Tm，其中每一个集合本身又是一棵树，并称为根的子树（SubTree）。

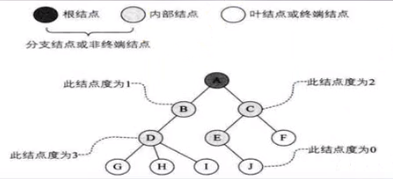
节点的度：节点拥有子树数称为节点的度。（也就是该节点拥有的子节点数）度为0的节点称为非终端节点或分支节点，除根节点外，分支节点也称为内部节点，树的度是树内各节点度的最大值。

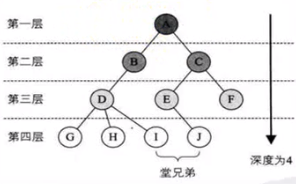
节点的层次与深度：节点的层次（Level）从根开始定义，根为第一层，根的孩子为第二层。若A节点在第l层，则其子树的根就在第l+1层（即A节点的子节点）。其双亲在同一层的节点互为堂兄弟。树中节点的最大层次称为树的深度（Depth）或高度。

树的存储结构

简单的顺序存储不能满足树的实现，需要结合顺序存储和链式存储实现。
三种表示方法：

• 双亲表示法
• 孩子表示法
• 孩子兄弟表示法
• 孩子双亲表示法

双亲表示法：

在每个节点中，附设一个指示器，指示其双亲节点在链表中的位置。


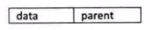
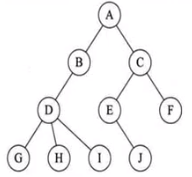
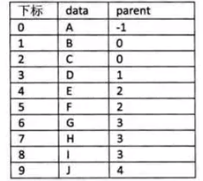
缺点：找父节点容易，找子节点难。

孩子表示法：

方案一：

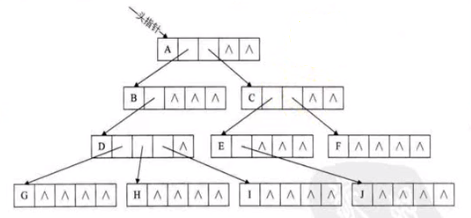
缺点：大量空指针造成浪费
方案二：

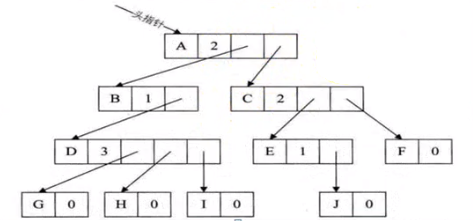
缺点：维护困难，不易实现。
也未解决找父节点容易，找子节点难的问题。

孩子兄弟表示法

任意一棵树，他的结点的第一个孩子如果存在就是唯一结点，他的右兄弟如果存在，也是唯一的，因此，我们设置两个指针，分别指向该结点的第一个孩子和该结点的右兄弟（I不是G的右兄弟）

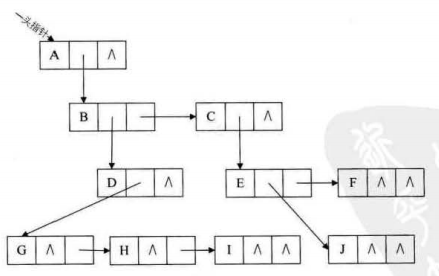
孩子双亲表示法

用顺序存储和链式存储组合成散列链表，可以通过获取头指针获取该元素父节点。

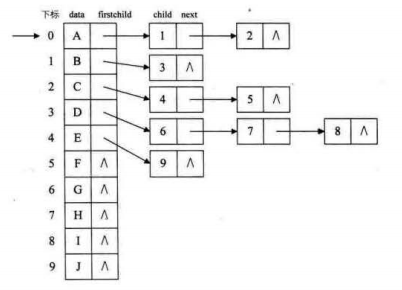
不太清楚？那就将元素的父节点单独列出来：

---

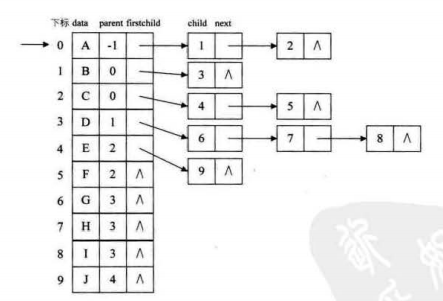
二叉树

二叉树是每个结点最多有两个子树的树结构

斜树

所有节点都只有左子树的二叉树叫做左斜树。所有节点都只有右子树的二叉树叫做右斜树。两者统称为斜树。

线性表结构可以理解为树的一种表达形式。

满二叉树

所有分支节点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

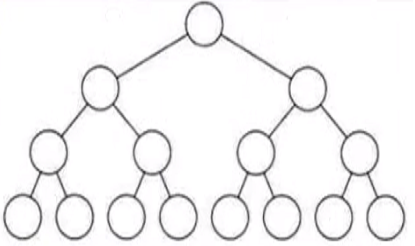
完全二叉树

对于一个有n个节点的二叉树按层序编号，如果编号为i（1 ≤ i ≤ n）的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同则该二叉树称为完全二叉树。

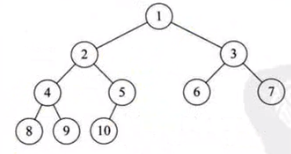
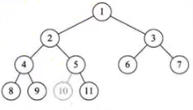
二叉树的性质：

• 性质1：二叉树第i层上的结点数目最多为 2^i-1 ( i ≥1 )。
• 性质2：深度为k的二叉树至多有2^k-1个结点( k ≥ 1 )。
• 性质3：包含n个结点的二叉树的深度至少为log₂ (n+1)。
• 性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1。
• 性质5：对于一个有n个节点的完全二叉树（深度为log₂ (n+1)），节点按层序编号（从第一层到log₂ (n+1)，每层从左到右），对任意一个节点i有：对于第i个非根节点，其父节点是第i/2个。

Java实现二叉树及其遍历

这里我们采用的结构是二叉链表：

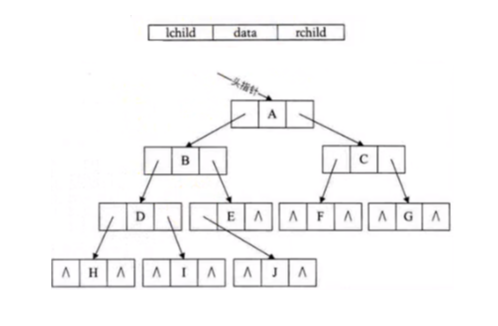
新建一个BinaryTree的类，并初始化一个测试树：

class BinaryTree

public class BinaryTree {
    private Node root=null;

    public void createTestBinaryTree(){
        /**
         *            A
         *           /  
         *          B    C
         *        /       
         *       D    E     F
         *
         */
        root=new Node(1,"A");
        Node nodeB=new Node(2,"B");
        Node nodeC=new Node(3,"C");
        Node nodeD=new Node(4,"D");
        Node nodeE=new Node(5,"E");
        Node nodeF=new Node(6,"F");
        root.leftChild=nodeB;
        root.rightChild=nodeC;
        nodeB.leftChild=nodeD;
        nodeB.rightChild=nodeE;
        nodeC.rightChild=nodeF;
        //这么写太蠢了。以后再更新二叉树的构建。。。
    }

    //由数组构造二叉树。
    public void createTestBinaryTree2(){
    /**
        *            A
        *           /  
        *          B    C
        *        /     /
        *       D    E F
        *
        */

    String[] strings=new String[]{"A","B","C","D","E","F"};
    List<Node> nodes=new ArrayList<>();
    for (int i = 0; i < strings.length; i++) {
        Node node = new Node(i,strings[i]);
        nodes.add(node);
    }
    root=nodes.get(0);
    //如果root为第一个节点，则第i个节点的左子节点是第2i个
    //这里i是从0开始的
    for (int i = 0; i < nodes.size(); i++) {
        if ((2*i+1)<nodes.size()){
            nodes.get(i).leftChild=nodes.get(2*i+1);
        }
        if ((2*i+2)<nodes.size()){
            nodes.get(i).rightChild=nodes.get(2*i+2);
        }
    }
}

根据该结构构造其节点类与get方法：

class Node

public class Node<T>{
    private int index;
    private T data;
    private Node leftChild;
    private Node rightChild;

    public Node(int index,T data){
        this.index=index;
        this.data=data;
        this.leftChild=null;
        this.rightChild=null;
    }

    public int getIndex() {
        return index;
    }

    public T getData() {
        return data;
    }
}

然后是树深度和节点数的方法：

height方法和size方法

public int height(){
    return getHeight(root);
}

private int getHeight(Node node){
    if (node ==null){
        return 0;
    }else {
        int i=getHeight(node.leftChild);
        int j=getHeight(node.rightChild);
        return i>j?i+1:j+1;//遍历1层就增加了1，i和j哪个大返回哪个
    }
}
public int size(){
    return getsize(root);
}

private int getsize(Node node){
    if (node==null){
        return 0;
    }else {
        return 1+getsize(node.leftChild)+getsize(node.rightChild);//遍历一个节点增加1，最后总数就是节点数
    }
}

接着就是四种遍历方法：先序遍历、中序遍历、后序遍历，层序遍历。先序、中序、后序是指root节点出现的方式。比如一个只有三个节点的二叉树，先序就是先遍历读取根节点，再左再右；中序就是先左，后根，然后右，后序先左后右，最后根。层序就是从上到下、从左到右依次读取。
比较简单容易理解的方式是递归：

先序遍历（递归）

public void preOrder(){
    preOrder(root);
    return;
}

private void preOrder(Node node){
    if (node==null){
        return;
    }else{
        System.out.println("先序遍历："+node.data);
    }
    if (node.leftChild!=null){
        preOrder(node.leftChild);
    }
    if (node.rightChild!=null){
        preOrder(node.rightChild);
    }
}

…………

中序遍历（递归）

public void midOrder(){
    midOrder(root);
    return;
}

private void midOrder(Node node){
    if (node.leftChild!=null){
        midOrder(node.leftChild);
    }
    if (node==null){
        return;
    }else{
        System.out.println("中序遍历："+node.data);
    }
    if (node.rightChild!=null){
        midOrder(node.rightChild);
    }
}

…………

后序遍历（递归）

public void postOrder(){
    postOrder(root);
    return;
}

private void postOrder(Node node) {
    if (node.leftChild != null) {
        postOrder(node.leftChild);
    }

    if (node.rightChild != null) {
        postOrder(node.rightChild);
    }

    if (node==null){
        return;
    }else{
        System.out.println("后序遍历："+node.data);
    }
}

三种遍历都能用递归的方式，但是递归运行效率较低，并且树大了之后很容易溢出，可以用栈和循环代替递归：
（我为什么写这么啰嗦，以为博客园的折叠不能挨着，中间必须有中文字符！！！）

先序遍历（栈）

public void nonRecPreOrder(){
    nonRecPreOrder(root);
    return;
}

private void nonRecPreOrder(Node node){
    if (node==null){
        return;
    }
    Stack<Node> stack=new Stack<>();
    stack.push(node);
    while (!stack.isEmpty()){
        Node theNode=stack.pop();
        if (theNode.rightChild!=null){
            stack.push(theNode.rightChild);
        }
        if (theNode.leftChild!=null){
            stack.push(theNode.leftChild);
        }
        System.out.println("先序遍历（栈）："+theNode.data);
    }
}

…………

先序遍历2（栈）

public void nonRecPreOrder2() {
    nonRecPreOrder2(root);
    return;
}

private void nonRecPreOrder2(Node node) {
    //非递归实现
    Stack<Node> stack = new Stack<>();
    while (node != null || !stack.isEmpty()) {
        while (node != null) {
            System.out.println("先序遍历2（栈）:" + node.data);
            stack.push(node);
            node = node.leftChild;
        }
        if (!stack.isEmpty()) {
            node = stack.pop();
            node = node.rightChild;
        }
    }
}

…………

中序遍历（栈）

public void nonRecMidOrder(){
    nonRecMidOrder(root);
    return;
}
private void nonRecMidOrder(Node node){
    if (node==null){
        return;
    }
    Stack<Node> stack=new Stack<>();
    Node p = root;//辅助节点
    stack.add(p);
    while(!stack.isEmpty()) {
        //只要你有左孩子，就将左孩子压入栈中
        if(p!=null &&  p.leftChild!=null) {
            stack.add(p.leftChild);
            p=p.leftChild;
        }else {
            p = stack.pop();//弹出栈顶节点  左孩子--->根节点
            System.out.println("中序遍历（栈）"+p.data);//访问
            if(p!=null && p.rightChild!=null) {//如果栈点元素有右孩子的话，将有节点压入栈中
                stack.push(p.rightChild);
                p = p.rightChild;
            }else
                p = null;//p=stk.pop;已经访问过p了，p设置为null
        }
    }
}

…………

中序遍历2（栈）

public void nonRecMidOrder2() {
    nonRecMidOrder2(root);
    return;
}

private void nonRecMidOrder2(Node node) {
    //中序遍历费递归实现
    Stack<Node> stack = new Stack<>();
    while (node != null || !stack.isEmpty()) {
        while (node != null) {
            stack.push(node);
            node = node.leftChild;
        }
        if (!stack.isEmpty()) {
            node = stack.pop();
            System.out.println(node.data);
            node = node.rightChild;
        }
    }
}

…………

后序遍历（栈）

public void nonRecPostOrder() {
    nonRecPostOrder(root);
    return;
}

private static void nonRecPostOrder(Node biTree) {
    //后序遍历非递归实现
    int left = 1;//在辅助栈里表示左节点
    int right = 2;//在辅助栈里表示右节点
    Stack<Node> stack = new Stack<>();
    Stack<Integer> stack2 = new Stack<>();//辅助栈，用来判断子节点返回父节点时处于左节点还是右节点。

    while (biTree != null || !stack.empty()) {
        while (biTree != null) {//将节点压入栈1，并在栈2将节点标记为左节点
            stack.push(biTree);
            stack2.push(left);
            biTree = biTree.leftChild;
        }

        while (!stack.empty() && stack2.peek() == right) {//如果是从右子节点返回父节点，则任务完成，将两个栈的栈顶弹出
            stack2.pop();
            System.out.println(stack.pop().data);
        }

        if (!stack.empty() && stack2.peek() == left) {//如果是从左子节点返回父节点，则将标记改为右子节点
            stack2.pop();
            stack2.push(right);
            biTree = stack.peek().rightChild;
        }
    }
}

…………

层次遍历（队列）

public void levelOder(){
    levelOrder(root);
    return;
}

private void levelOrder(Node node){
//层次遍历
/*
1.对于不为空的结点，先把该结点加入到队列中
2.从队中拿出结点，如果该结点的左右结点不为空，就分别把左右结点加入到队列中
3.重复以上操作直到队列为空
*/
    if(node == null)
        return;
    LinkedList<Node> list = new LinkedList<Node>();
    list.add(node);
    Node currentNode;
    while(!list.isEmpty()) {
        currentNode = list.poll();
        System.out.println("层序遍历（队列）"+currentNode.data);
        if(currentNode.leftChild != null)
            list.add(currentNode.leftChild);
        if(currentNode.rightChild != null)
            list.add(currentNode.rightChild);
    }
}

这里，后序遍历和层次遍历参考了这个博客，特别是后序遍历，笔者对于递归函数非递归化还有待提高，递归函数虽然简单易懂，但是数据量大了之后特别容易爆栈，所有的递归函数都可以非递归化，因此优先考虑非递归函数。
树是一种重要的数据结构类型，通过对二叉树的研究，笔者对栈的用法有了更深的理解。