二叉树的遍历
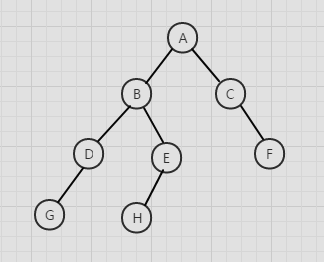
二叉树的前序遍历
访问根结点,先序遍历左子树,先序遍历右子树
遍历基本步骤为先根结点,然后左子树,然后右子树, 需要注意的是这个遍历需要类似于递归,在访问完A以后,需要去访问B,这时,需要把B当做一个根结点,下一次应该去访问D而不是C,只到访问到G即叶子节点以后才会递归的往回访问,所有节点都可以看作为父节点,叶子节点可以看做两个孩子为空的父节点
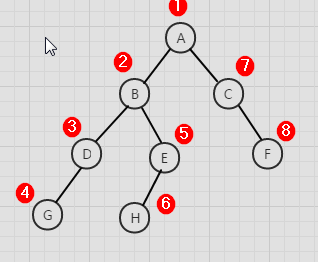
二叉树的中序遍历
中序遍历左子树,访问根结点,中序遍历右子树
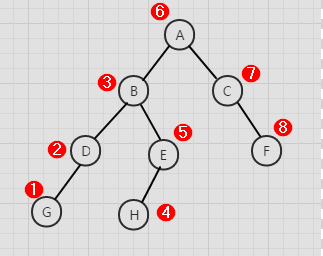
二叉树的后续遍历
后续遍历左子树,后续遍历右子树,访问根结点。
后选遍历为先遍历左子树,若其节点有左子树,则会往下递归找到最后一个左子树开始,然后遍历右子树,如果右子树有子节点,将会按照前面的方法进行遍历。
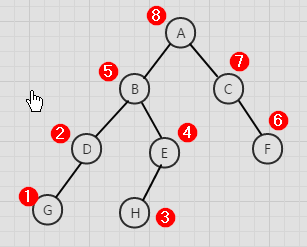
建立二叉树
public void buildTree(Node node) {
Scanner in = new Scanner(System.in);
String str = in.next();
System.out.println(str);
if ("#".equals(str)) {
node = null;
} else {
node.data = str;
buildTree(node.left = new Node(""));
buildTree(node.right = new Node(""));
}
}
上图应输入:ABDG###EH###C#F## (#代表空节点)
二叉树的前、中、后遍历(递归遍历)
存储结构
class Node {
public Node left;
public Node right;
public String data;
public Node(String data) {
this.left = null;
this.right = null;
this.data = data;
}
}
二叉树的前序遍历(递归)
public void preOrder(Node node) {
if (node != null) {
System.out.print(node.data);
preOrder(node.left);
preOrder(node.right);
}
}
二叉树的中序遍历(递归)
public void postOrder(Node node) {
if (node != null) {
postOrder(node.left);
postOrder(node.right);
System.out.print(node.data);
}
}
二叉树的后续遍历(递归)
public void inOrder(Node node) {
if (node != null) {
inOrder(node.left);
System.out.print(node.data);
inOrder(node.right);
}
}
二叉树的非递归实现
因为当遍历过根节点之后还要回来,所以必须将其存起来。考虑到后进先出的特点,选用栈存储。数量确定,以顺序栈存储。
前序遍历
// 需要将访问过的节点都记录下来,最后取出来在访问右子树
public void preOrder2(Node node) { // 通过栈来实现
Stack<Node> nodeS = new Stack<>();
if (node == null) {
System.out.println("数据错误");
} else {
while (!nodeS.isEmpty() || node != null) {
while (node != null) {
System.out.print(node.data); // 访问根结点
nodeS.push(node);
node = node.left;
}
node = nodeS.pop();
node = node.right;
}
}
}
中序遍历
public void postOrder2(Node node) {
Stack<Node> nodeS = new Stack<>();
if (node == null) {
System.out.println("数据错误");
} else {
while (!nodeS.isEmpty() || node != null) {
while (node != null) {
nodeS.push(node);
node = node.left;
}
node = nodeS.pop();
System.out.print(node.data);
node = node.right;
}
}
}
后序遍历
后序遍历的难点在于:需要判断上次访问的节点是位于左子树,还是右子树。若是位于左子树,则需跳过根节点,先进入右子树,再回头访问根节点;若是位于右子树,则直接访问根节点,这里解决方式是设置一个辅助栈用来标志当前节点的状态。
// 所以设置一个辅助栈 里面存放对应节点的状态
public void inOrder2(Node node) {
Stack<Node> nodeS = new Stack<>();
Stack<Boolean> tagS = new Stack<>(); // 辅助栈
boolean tag = false;
while (!nodeS.isEmpty() || node != null) {
while (node != null) {
nodeS.push(node);
tagS.push(false); // 初始化,false代表第一次访问
node = node.left;
}
tag = tagS.pop(); // 先将节点对应的标志位出栈
if (tag) { // 判断,如果是true 代表第二次访问, 则出栈并且访问
node = nodeS.pop();
System.out.print(node.data);
node = null;
} else { // false, 则是第一次访问,需要访问右子树
tagS.push(true); // 则把标志位改为true,然后将标志压入栈中(上面标志位出栈了)
node = nodeS.lastElement(); // 获取到栈顶元素
node = node.right; // 右子树
}
}
}