P4005 小 Y 和地铁

Luogu4005

题解

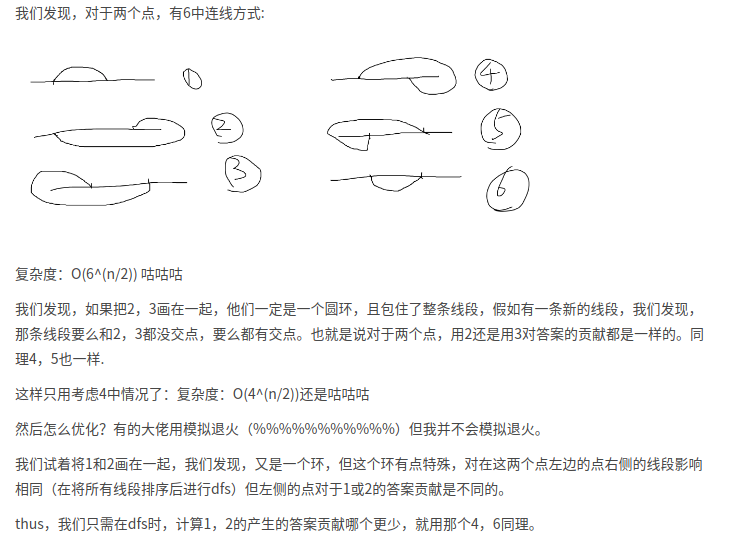
((2,3);(4,5))对之后的影响是等价的 , 所以只考虑往右边延伸的(2)和(4)

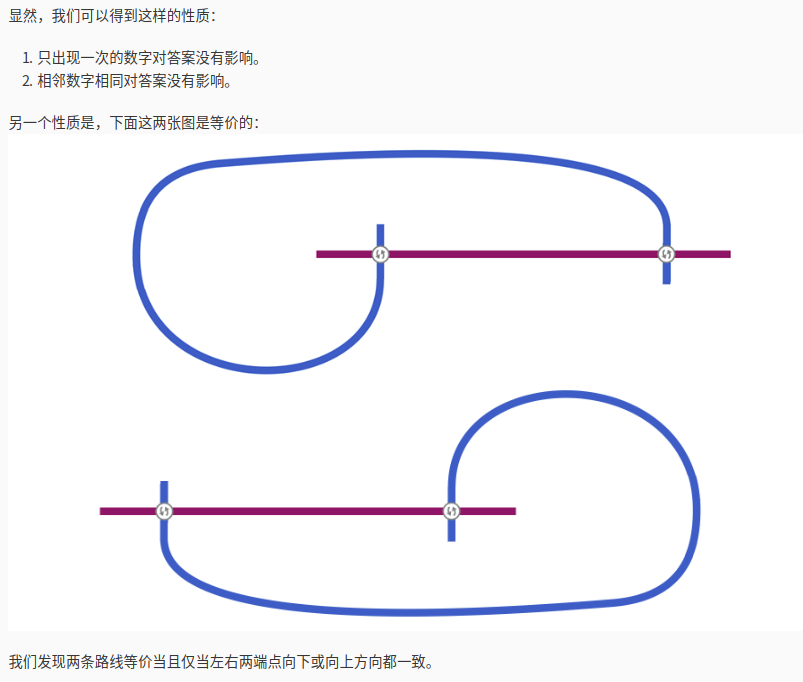
连接的时候这两个又是等价的 , 但是对之后的影响不同

考虑维护连接上下的区间需要穿过几条线 , 可以写出以下的代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int INF=1e9+7;
inline LL read(){
	register LL x=0,f=1;register char c=getchar();
	while(c<48||c>57){if(c=='-')f=-1;c=getchar();}
	while(c>=48&&c<=57)x=(x<<3)+(x<<1)+(c&15),c=getchar();
	return f*x;
}

const int N=51;

struct BIT{
	int a[N],n;
	inline void init(int x){
		for(int i=1;i<=x;i++) a[i]=0;
		n=x;
	}
	inline void insert(int x,int val){
		for(;x<=n;x+=x&-x) a[x]+=val;
	}
	inline int query(int l,int r){
		int res=0;
		for(int i=r;i;i-=i&-i) res+=a[i];
		for(int i=l-1;i;i-=i&-i) res-=a[i];
		return res;
	}
}up,down;

int a[N],l[N],r[N];
int T,n,cnt,ans;

inline void dfs(int cur,int sum){
	if(sum>ans) return;
	if(cur>cnt){
		ans=min(ans,sum);
		return;
	}
	up.insert(r[cur],1);
	dfs(cur+1,sum+min(up.query(l[cur],r[cur]-1),down.query(l[cur],n)+up.query(r[cur]+1,n)));
	up.insert(r[cur],-1);
	down.insert(r[cur],1);
	dfs(cur+1,sum+min(down.query(l[cur],r[cur]-1),up.query(l[cur],n)+down.query(r[cur]+1,n)));
	down.insert(r[cur],-1);
}

int main(){
	T=read();
	while(T--){
		n=read(),ans=INF,cnt=0;
		for(int i=1;i<=n;i++) a[i]=read();
		for(int i=1;i<=n;i++){
			for(int j=i+2;j<=n;j++)if(a[i]==a[j]){
				l[++cnt]=i,r[cnt]=j;
				break;
			}
		}
		up.init(n);down.init(n);
		dfs(1,0);
		printf("%d
",ans);
	}
}