POJ3718 Facer's Chocolate Dream

本文版权归ljh2000和博客园共有，欢迎转载，但须保留此声明，并给出原文链接，谢谢合作。

本文作者：ljh2000
作者博客：http://www.cnblogs.com/ljh2000-jump/
转载请注明出处，侵权必究，保留最终解释权！

 

Description

"It is so sweet to have chocolates on St. Valentine's Day!" Little Facer was so excited when he receives a box of self-made chocolates from his girlfriend, and he decided to eat these chocolates in a special way to commemorate this important day. Suppose that there are N types of chocolates in the box, it can be easily calculated that there are totally 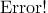 different combinations if we choose 3 chocolates of different types to make a dish. Facer will first make one dish for every of these combination, so there will be 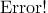dishes in all with 3× 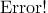chocolates totally. Then both Facer and his girlfriend choose some chocolates of different types as their original chocolates set. After that, Facer choose exactly M dishes of three-type-mixed-chocolates which he made in the first step and add them into his original chocolates set. Finally, Facer continues eatting two chocolates of the same type until he cannot find any pair of chocolates of the same type (which means for each type of chocolates, there remains at most one chocolate). Facer wishes that his remaining chocolates set could be identical with his girlfriend's original chocolates set after the steps mentioned above, but he does not know the number of ways to choose dishes. Could please tell him the answer?

Input

The input consists of multiple test cases. Each test case starts with two integers, N and M, which are the number of different types of chocolates and the number of three-type-mixed-chocolates dishes Facer will choose, it is guaranteed that 1≤N≤1000, 0≤M≤1000. The following two lines contain one N-bit binary integer each, which represents Facer's and his girlfriend's original chocolates set. A case with N=0 and M=0 indicates the end of the input file, which should not be processed.

Output

For each test case, print one line containing one single integer, which represents the total number of ways to choose dishes. Since the number can be extremely big, you are only required to output the answer % 10007.

Sample Input

4 3
1101
1001
3 1
101
010
5 3
11010
10111
0 0

Sample Output

1
1
6

 

 

正解：数学+DP

解题报告：

　　

　　

//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
using namespace std;
typedef long long LL;
#define RG register
const int MOD = 10007;
const int MAXN = 1511;
int n,m,ni[MAXN],cnt;
LL f[MAXN][MAXN],C[MAXN][5];
char ch[MAXN],s[MAXN];
bool vis[MAXN][MAXN];
//f[m][t]=(1/m)*( (i=1->3 f[m-1][t+2*i-3]*C(n-t,3)*C(t,3-i)) - f[m-2][t]*(C[n][3]-m+2) )

inline int getint(){
    int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
    if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}

inline LL getf(RG int M,RG int N){
	if(N<0 || M<0) return 0; if(M==0 && N!=0) return 0;
	if(M>m || N>n) return 0;
	if(vis[M][N]) return f[M][N]; vis[M][N]=1; f[M][N]=0;
	RG LL now;
	//1: -3
	now=getf(M-1,N+3)*C[n-N][3]; now%=MOD;
	f[M][N]+=now; f[M][N]%=MOD;

	//2: -1
	now=getf(M-1,N+1)*C[n-N][2]; now%=MOD;
	now*=C[N][1]; now%=MOD;
	f[M][N]+=now; f[M][N]%=MOD;

	//3: +1
	now=getf(M-1,N-1)*C[n-N][1]; now%=MOD;
	now*=C[N][2]; now%=MOD;
	f[M][N]+=now; f[M][N]%=MOD;

	//4: +3
	now=getf(M-1,N-3)*C[N][3]; now%=MOD;
	f[M][N]+=now; f[M][N]%=MOD;

	//算重
	now=getf(M-2,N); now*=(C[n][3]-(M-2)); now%=MOD;
	//now*=(M-1); now%=MOD;
	f[M][N]-=now; f[M][N]%=MOD;

	f[M][N]+=MOD; f[M][N]%=MOD;
	f[M][N]*=ni[M];
	f[M][N]%=MOD;

	return f[M][N];
}

inline void work(){
	for(int i=0;i<=1000;i++) C[i][0]=1;
	for(int i=1;i<=1000;i++) 
		for(int j=1;j<=min(i,3);j++)
			C[i][j]=C[i-1][j-1]+C[i-1][j],C[i][j]%=MOD;

	for(RG int i=1;i<=1000;i++)
		for(RG int j=1;j<MOD;j++)
			if((i*j%MOD) == 1) { 
				ni[i]=j; 
				break;
			} 

	while(1) {
		n=getint(); m=getint(); if(n==0 && m==0) break;
		scanf("%s",ch); scanf("%s",s); cnt=0;
		for(RG int i=0;i<n;i++) if(ch[i]!=s[i]) cnt++;
		memset(vis,0,sizeof(vis)); memset(f,0,sizeof(f));
		vis[0][0]=1; f[0][0]=1;
		printf("%lld
",getf(m,cnt));
	}
}

int main()
{
    work();
    return 0;
}