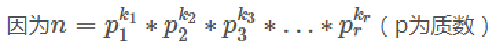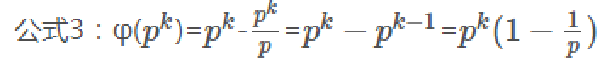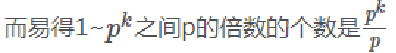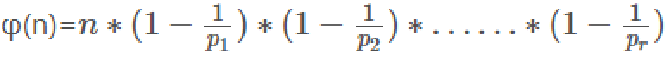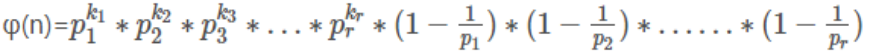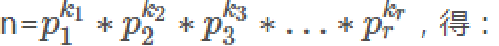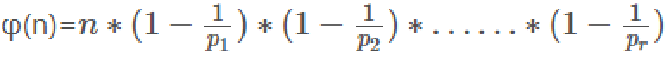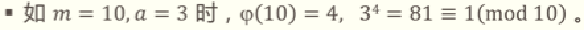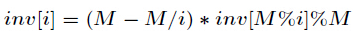同余基本概念
剩余系
欧拉函数
欧拉函数φ(n)表示1~n中所有与n互质的数。比如1~8中与8互质的数有1,3,5,7,所以φ(8)=4。
公式1:如果p是素数,有φ(p)=p-1。
公式2(积性):如果(a,b)=1,有φ(a*b)=φ(a)*φ(b),
--->以下是公式二的证明过程
设模a的一个简系为a1,a2,a3,…,aφ(a),模b的一个简系为b1,b2,b3,…,bφ(b) 现在我们要证明:所有ai∗b+bj∗a(共φ(a)*φ(b)个)组成了模a*b的一个简系(即φ(a*b)=φ(a)*φ(b))。 判定简系需要证明下面三点:
-
(ai∗b+bj∗a,a∗b)=1。
-
ai∗b+bj∗a≢ak∗b+bt∗a(mod a∗b)(i!=k或j!=t)
-
对于任意k满足(k,a*b)=1,则一定有k≡ai∗b+bj∗a(mod a∗b)(即没有遗漏)
证明1: (ai∗b+bj∗a,a∗b)=1。
因为(a,ai)=1,(a,b)=1,所以(a,ai*b)=1,由辗转相除法可得(a,ai*b+bj*a)=(a,ai*b)=1,同理得(b,ai*b+bj*a)=1。 所以1得证。
证明2: ai∗b+bj∗a≢ak∗b+bt∗a(mod a∗b)(i!=k或j!=t)
证明3: 对于任意k满足(k,a*b)=1,则一定有k≡ai∗b+bj∗a(mod a∗b)
所以φ(n)是积性函数(但不是完全积性,因为要满足(a,b)=1)。 有了这个公式,就可以推得欧拉函数的通项公式。
又因任意两个p互质(没有共同质因子),
所以: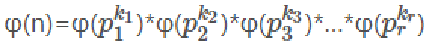
公式4:欧拉函数的通项公式
由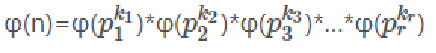
求欧拉函数值
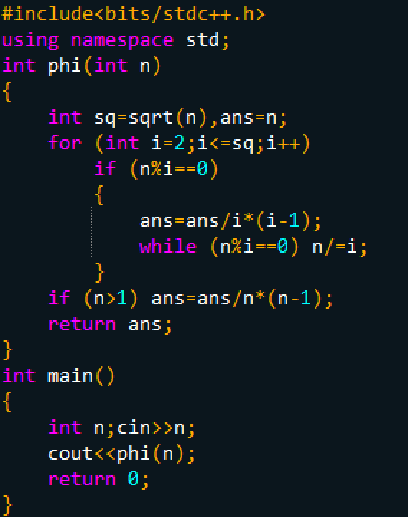
1.如果只求φ(n),唯一分解 那么我们就直接将n唯一分解处理出每一个n的素数,然后用通项公式就行了。 效率:O(√n)
2、如果要求φ(1~n) 用唯一分解就比较慢了,所以我们可以用筛法求出φ(1~n),原理和筛素数是一样的。普通筛法用到的是通项公式,而线性筛法用到公式1、公式2(积性)和公式3。
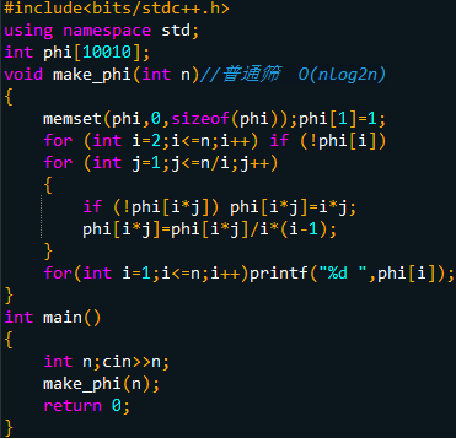
普通筛法代码:
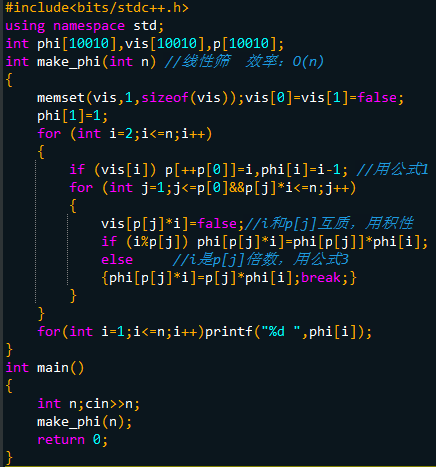
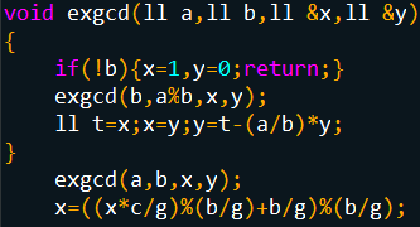
线性筛法代码:
解释一下上面代码make_phi函数里的第一个循环(下图中的x即循环中的i)
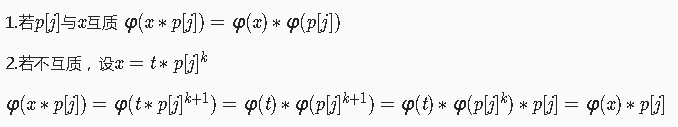
这里附几道求欧拉函数值的习题:
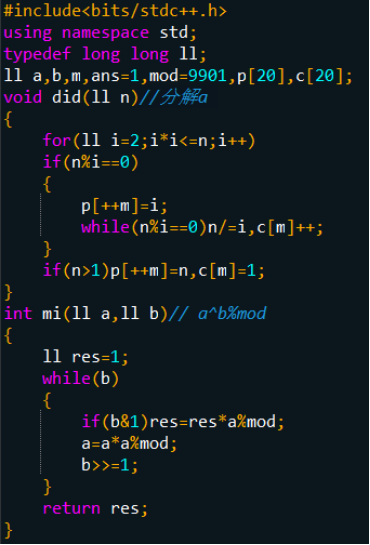
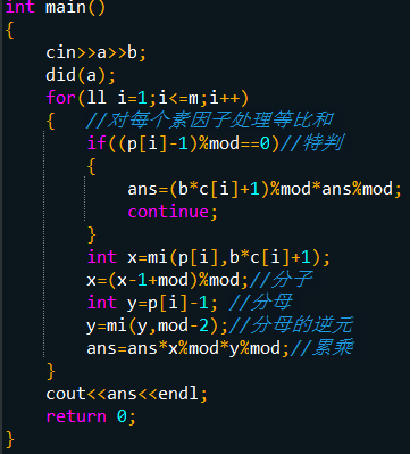
洛谷 P2303 [SDOi2012]Longge的问题
--->题解
洛谷 P2568 GCD
--->题解
模运算
【同余的几个性质】
性质1:a≡a(mod m),(自反性)
性质2:若a≡b(mod m),那么b≡a(mod m)(对称性)
性质3:若a≡b(mod m),b≡c(mod m)=>a≡c(mod m)(传递性)
性质4:若a≡b(mod m),c≡d(mod m),那么a±c≡b±d(mod m)(可加减性)
证明:设a=A+Ka*m,b=A+Kb*m,c=C+Kc*m,d=C+Kd*m则(a±c)%m=(A±C),(b±d)%m=(A±C)即a±c≡b±d(mod m)
性质5:若a≡b(mod m),c≡d(mod m),那么ac≡bd(mod m)(可乘性)
证明:设a=A+Ka*m,b=A+Kb*m,c=C+Kc*m,d=C+Kd*m则ac=( A+Ka*m)( C+Kc*m),bd=( A+Kb*m)( C+Kd*m)所以ac%m=AC bd%m=AC即ac≡bd(mod m)
性质6:若a≡b(mod m),那么an≡bn(mod m)(其中n为自然数)
证明:由性质1和性质5得。
性质7:若ac≡bc(mod m),(c,m)=1,那么a≡b(mod m)
证明:ac≡bc(mod m)=>c(a-b)≡0(mod m)=>c%m*(a-b)%m=0 =>m|c或m|(a-b)又因为(m,c)=1.所以m|(a-b)即a≡b(mod m)
性质8:若a≡b(mod m),那么a^t≡b^t(mod m)
证明:由性质5得。
性质9:若 a≡b(mod m1) a≡b(mod m2)…. a≡b(mod mk) 则 a≡b(mod [m1,m2……mk])
证明:由题意得mi|(a-b) (1<=i<=k)即(a-b)是mi的公倍数,所以[m1,m2……mk]|(a-b)即a≡b(mod [m1,m2……mk])
欧拉定理
若正整数a、n互素,有: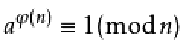
消去律:如果 gcd(c,p) = 1 ,则 ac ≡ bc mod p ⇒ a ≡ b mod p 。
费马小定理
若正整数 a 与素数 p 互质,则有 a^(p-1) ≡ 1 mod p。
证明这个定理非常简单,由于 φ(p) = p -1,代入欧拉定理即可证明。
欧拉定理的推论
扩展欧几里得算法
欧几里得定理,即gcd(a,b)=gcd(b,a mod b)
定理1:如果a、b是不全为0的整数,那么一定存在整数x、y使得ax+by=gcd(a,b)。
对于线性同余方程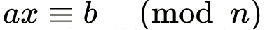
可以改写成ax+ny=b的形式
如何求解 (以下讨论a>b):
当 b=0,gcd(a,b)=a。此时 x=1,y=0;(特解)
当a>b>0 时 设 ax1+ by1= gcd(a,b);
bx2+ (a mod b)y2= gcd(b,a mod b);
根据欧几里德原理有 gcd(a,b) = gcd(b,a mod b);
则:ax1+ by1= bx2+ (a mod b)y2;
即:ax1+ by1= bx2+ (a - [a / b] * b)y2 = ay2+ bx2- [a / b] * by2;
(a mod b = a - [a / b]*b;[a / b]为a整除b) 也就是ax1+ by1 = ay2 + b(x2- [a / b] *y2);
根据恒等定理得:x1=y2;y1=x2- [a / b] *y2;
这样就得到了求解 x1,y1 的方法:x1,y1 的值基于 x2,y2 :
引理:
ax+by = z,z为gcd(a,b)若干倍,求方程的解;
先求解ax+by = gcd(a,b),再将求出的解乘以 z/gcd(a,b)就好了。
求得了方程ax+by=gcd的一组特解为x0,y0;
通解:
-
如果a,b互质通解为x=x0+b*t, y=y0-a*t;
-
如果a,b不互质通解为x=x0+b/gcd*t, y=y0-a/gcd*t;