2.3.8Quick.sort()在处理N个全部重复的元素时大约需要多少次比较?
答:N(lgN-1)-lgN,一个更精确试验数据是:N(lgN-1)+2,目前没法分析出这个结果。
1)对于每个元素个数大于1的子数组,数组的第一个元素作为分界元素,然后从第二个元素和最后一个元素开始向中间移动,当左右两指针相邻,即左指针i+1=右指针j时,这段的每个元素与这个分界元素进行了一次对比,这段的元素个数为子数组元素个数-1,那么对比次数为这个子数组元素个数-1次。
在左右两指针相邻的情况下,如果这个子数组元素个数为奇数,左指针i向前推进一位,此时会再进行一次对比,推进后满足左指针i=右指针j,这个子数组的对比就完成了。
在左右两指针相邻的情况下,如果这个子数组元素个数为偶数,右指针j向前推进一位,此时会再进行一次对比,推进后满足左指针i=右指针j,这个子数组的对比就完成了。
子数组的对比次数=左右指针相邻时对比次数+左指针或右指针向前推进1位时对比的1次=(子数组的元素个数-1)+1=子数组的元素个数
2)子数组只有1个元素时对比次数为0。
3)第1层时,有1个子数组,长度为N,这一层的对比次数为N。
3)第2层时,有2个子数组,上一层的j位置元素不在这2个子数组中,此层的元素个数=上一层元素个数减1=N-1,此层的对比次数为N-1。
4)第3层时,有4个子数组,上一层2个子数组各有一个位置j的元素不在这4个子数组中,此层的元素个数为上一层的元素个数减2=(N-1)-2,此层的对比次数为(N-1)-2。
5)第4层时,有8个子数组,上一层4个子数组各有一个位置j的元素不在这8个子数组中,此层的元素个数为上一层的元素个数减4=((N-1)-2)-4,此层的对比次数为((N-1)-2)-4。
6)归纳得:子数组长度大于1时,每层的对比次数是上一层元素个数-上一层子数组个数。
7)由于子数组长度大于1时才有比较,所以有比较的层次数是 1(顶层)+lgN-1(底层)=lgN。
8)顶层有对比,但未减少元素。底层没有对比。倒数第二层的减少元素数与倒数第三层相关,那么有减少元素个数的层数有lgN-1(底层)-1(倒数第二层)=lgN-2
9)将第6点的归纳,按下面的方式来求对比次数
总的对比次数=N*对比层数 - 各层的元素减少数之和
总的对比次数=N*lgN - 各层的元素减少数之和
各层的减少元素个数如下:
1=2^0=2^1-1
1+2=2^0+2^1=2^2-1
1+2+4=2^0+2^1+2^2=2^3-1
...
1+2+4+...2^(lgN-2)=2^(lgN-1)-1
所有项求和之前先看下面的闭公式推导
x1=2^1-1=2^0
x2=2^2-1=2^0+2^1
x3=2^3-1=2^0+2^1+2^2
x4=2^4-1=2^0+2^1+2^2+2^3
xn=2^(n+1)-1=2^0+2^1+2^2+2^3+2^n
S=x1+x2+x3+x4+...xn
S=(2^1-1)+(2^2-1)+(2^3-1)+(2^4-1)+...(2^(n+1)-1)
S=2^1+2^2+2^3+2^4+...2^(n+1)-n*1
S=2^0-2^0+2^1+2^2+2^3+2^4+...2^(n+1)-n*1
S=2^(n+2)-1-2^0-n*1
S=2^(n+2)-1-1-n
S=2^(n+2)-n-2
按此闭公式得各层的减少元素个数和为
2^(lgN-2+2)-(lgN-2)-2
=2^lgN-lgN
=N-lgN
再代入总的对比次数=N*lgN-N-lgN
=N(lgN-1)-lgN
10)试验结果:
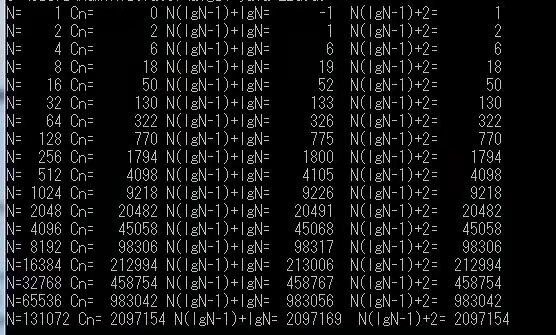
11)试验代码:
public class E2d3d8
{
static int Cn=0;
public static void sort(Comparable[] a)
{
Cn=0;
StdRandom.shuffle(a);
sort(a,0,a.length-1);
StdOut.printf("N=%5d Cn=%8d N(lgN-1)+lgN=%8.0f N(lgN-1)+2=%8.0f ",a.length,Cn,a.length*(Math.log(a.length)/Math.log(2)-1)+Math.log(a.length)/Math.log(2),a.length*(Math.log(a.length)/Math.log(2)-1)+2);
}
private static void sort(Comparable[] a,int lo,int hi)
{
if (hi<=lo) return;
int j=partition(a,lo,hi);
sort(a,lo,j-1);
sort(a,j+1,hi);
}
private static int partition(Comparable[] a,int lo,int hi)
{
int i=lo,j=hi+1;
Comparable v=a[lo];
while(true)
{
while(less(a[++i],v)) if(i==hi) break;
while(less(v,a[--j])) if(j==lo) break;
if(i>=j) break;
exch(a,i,j);
}
exch(a,lo,j);
return j;
}
private static boolean less(Comparable v,Comparable w)
{ Cn++;return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j)
{
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a)
{
for (int i=0;i<a.length;i++)
StdOut.print(a[i]+" ");
StdOut.println();
}
public static boolean isSorted(Comparable[] a)
{
for (int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;
return true;
}
public static void main(String[] args)
{
int N=1;
for (int i=0;i<18;i++)
{
Double[] a=new Double[N];
for(int j=0;j<a.length;j++)
a[j]=0.0;
sort(a);
N=2*N;
}
}
}
答:N(lgN-1)-lgN,一个更精确试验数据是:N(lgN-1)+2,目前没法分析出这个结果。
1)对于每个元素个数大于1的子数组,数组的第一个元素作为分界元素,然后从第二个元素和最后一个元素开始向中间移动,当左右两指针相邻,即左指针i+1=右指针j时,这段的每个元素与这个分界元素进行了一次对比,这段的元素个数为子数组元素个数-1,那么对比次数为这个子数组元素个数-1次。
在左右两指针相邻的情况下,如果这个子数组元素个数为奇数,左指针i向前推进一位,此时会再进行一次对比,推进后满足左指针i=右指针j,这个子数组的对比就完成了。
在左右两指针相邻的情况下,如果这个子数组元素个数为偶数,右指针j向前推进一位,此时会再进行一次对比,推进后满足左指针i=右指针j,这个子数组的对比就完成了。
子数组的对比次数=左右指针相邻时对比次数+左指针或右指针向前推进1位时对比的1次=(子数组的元素个数-1)+1=子数组的元素个数
2)子数组只有1个元素时对比次数为0。
3)第1层时,有1个子数组,长度为N,这一层的对比次数为N。
3)第2层时,有2个子数组,上一层的j位置元素不在这2个子数组中,此层的元素个数=上一层元素个数减1=N-1,此层的对比次数为N-1。
4)第3层时,有4个子数组,上一层2个子数组各有一个位置j的元素不在这4个子数组中,此层的元素个数为上一层的元素个数减2=(N-1)-2,此层的对比次数为(N-1)-2。
5)第4层时,有8个子数组,上一层4个子数组各有一个位置j的元素不在这8个子数组中,此层的元素个数为上一层的元素个数减4=((N-1)-2)-4,此层的对比次数为((N-1)-2)-4。
6)归纳得:子数组长度大于1时,每层的对比次数是上一层元素个数-上一层子数组个数。
7)由于子数组长度大于1时才有比较,所以有比较的层次数是 1(顶层)+lgN-1(底层)=lgN。
8)顶层有对比,但未减少元素。底层没有对比。倒数第二层的减少元素数与倒数第三层相关,那么有减少元素个数的层数有lgN-1(底层)-1(倒数第二层)=lgN-2
9)将第6点的归纳,按下面的方式来求对比次数
总的对比次数=N*对比层数 - 各层的元素减少数之和
总的对比次数=N*lgN - 各层的元素减少数之和
各层的减少元素个数如下:
1=2^0=2^1-1
1+2=2^0+2^1=2^2-1
1+2+4=2^0+2^1+2^2=2^3-1
...
1+2+4+...2^(lgN-2)=2^(lgN-1)-1
所有项求和之前先看下面的闭公式推导
x1=2^1-1=2^0
x2=2^2-1=2^0+2^1
x3=2^3-1=2^0+2^1+2^2
x4=2^4-1=2^0+2^1+2^2+2^3
xn=2^(n+1)-1=2^0+2^1+2^2+2^3+2^n
S=x1+x2+x3+x4+...xn
S=(2^1-1)+(2^2-1)+(2^3-1)+(2^4-1)+...(2^(n+1)-1)
S=2^1+2^2+2^3+2^4+...2^(n+1)-n*1
S=2^0-2^0+2^1+2^2+2^3+2^4+...2^(n+1)-n*1
S=2^(n+2)-1-2^0-n*1
S=2^(n+2)-1-1-n
S=2^(n+2)-n-2
按此闭公式得各层的减少元素个数和为
2^(lgN-2+2)-(lgN-2)-2
=2^lgN-lgN
=N-lgN
再代入总的对比次数=N*lgN-N-lgN
=N(lgN-1)-lgN
10)试验结果:
11)试验代码:
public class E2d3d8
{
static int Cn=0;
public static void sort(Comparable[] a)
{
Cn=0;
StdRandom.shuffle(a);
sort(a,0,a.length-1);
StdOut.printf("N=%5d Cn=%8d N(lgN-1)+lgN=%8.0f N(lgN-1)+2=%8.0f ",a.length,Cn,a.length*(Math.log(a.length)/Math.log(2)-1)+Math.log(a.length)/Math.log(2),a.length*(Math.log(a.length)/Math.log(2)-1)+2);
}
private static void sort(Comparable[] a,int lo,int hi)
{
if (hi<=lo) return;
int j=partition(a,lo,hi);
sort(a,lo,j-1);
sort(a,j+1,hi);
}
private static int partition(Comparable[] a,int lo,int hi)
{
int i=lo,j=hi+1;
Comparable v=a[lo];
while(true)
{
while(less(a[++i],v)) if(i==hi) break;
while(less(v,a[--j])) if(j==lo) break;
if(i>=j) break;
exch(a,i,j);
}
exch(a,lo,j);
return j;
}
private static boolean less(Comparable v,Comparable w)
{ Cn++;return v.compareTo(w)<0;}
private static void exch(Comparable[] a,int i,int j)
{
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a)
{
for (int i=0;i<a.length;i++)
StdOut.print(a[i]+" ");
StdOut.println();
}
public static boolean isSorted(Comparable[] a)
{
for (int i=1;i<a.length;i++)
if(less(a[i],a[i-1])) return false;
return true;
}
public static void main(String[] args)
{
int N=1;
for (int i=0;i<18;i++)
{
Double[] a=new Double[N];
for(int j=0;j<a.length;j++)
a[j]=0.0;
sort(a);
N=2*N;
}
}
}