参考的博客如下,谢谢这几篇文章,让我在理解EM算法的路上少走了许多弯路。
https://blog.csdn.net/v_july_v/article/details/81708386
https://www.cnblogs.com/bigmoyan/p/4550375.html
https://blog.csdn.net/u010834867/article/details/90762296
对应文档note8
The EM algorithm
Jensen’s inequality
设f是定义域为实数的函数
如果对于所有的实数x,f(x)的二次导数大于0,那么f是凸函数。
当x是向量时,如果其hessian矩阵H是半正定的(H>=0),那么f是凸函数。
如果f的二阶导大于0或者H>0,那么称f是严格凸函数
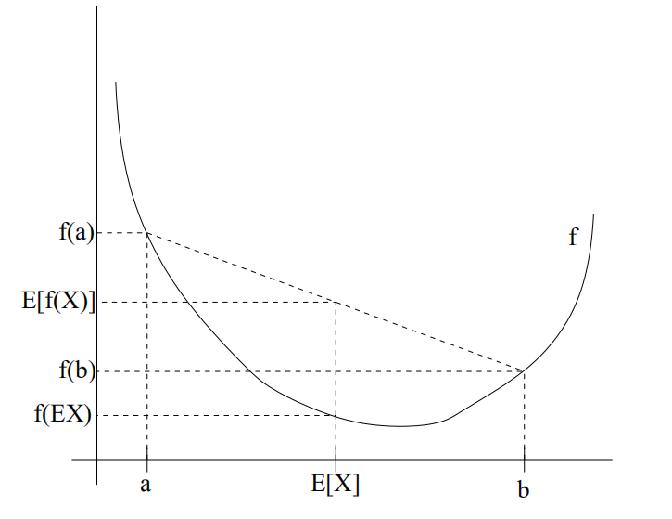
convex函数(凸函数):E[f(X)] ≥ f(EX). 在这里EX就代表E[X]均值。
特别地,当且仅当P(X = EX) = 1,即X是常量时, 上式取等号,即E[f(X)] = f(EX)。
同样,concave函数(凹函数):E[f(X)] ≤ f(EX)。
如图所示:实线f是凸函数, X是随机变量,有0.5的概率是a,有0.5的概率是b
- 最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
- 似然函数:它是给定样本值X下关于(未知)参数θ的函数。常说的概率是指给定参数后,预测即将发生的事件的可能性,然而似然函数关心不再是事件的发生概率,而是已知发生了某些事件,我们希望知道参数应该是多少。
- L(θ|x) = f(x|θ)
这里的x是指联合样本随机变量X取到的值,即X=x;
这里的θ是指未知参数;
这里的f(x|θ)是一个概率密度函数
- 最大似然函数:似然函数取得最大值表示相应的参数能够使得统计模型最为合理
- 假定已知某个参数B时,推测事件A会发生的概率写作
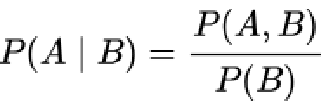
- 通过贝叶斯公式,可以得出
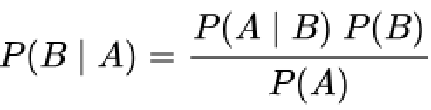
The EM algorithm
EM算法描述:
首先,初始化参数θ
(1)E-Step:根据参数θ计算每个样本属于zi的概率,这个概率就是Q
(2)M-Step:根据计算得到的Q,求出含有θ的似然函数的下界并最大化它,得到新的参数θ 重复(1)和(2)直到收敛。
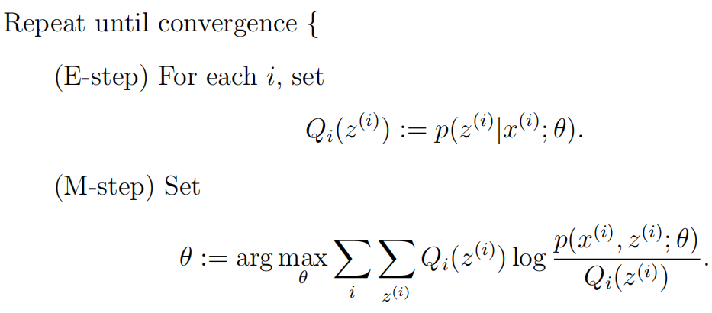
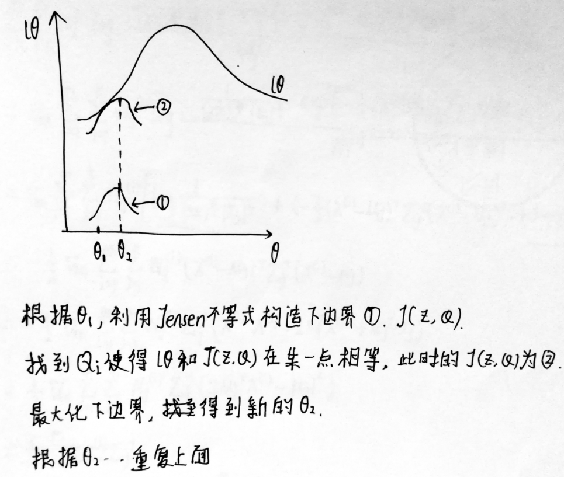
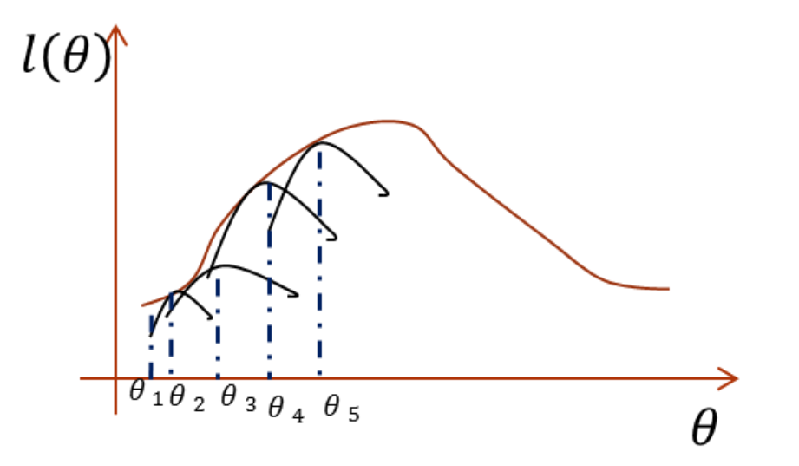
说起来不太容易理解,可以看下面的图理解一下。
左边的图:是初始化一个θ1,然后通过θ1利用Jensen不等式构造下边界J,当使下边界与对数似然函数有一点相等时,即到达圆圈2所在的状态,就最大化这个下边界,找到新的θ2,接着重复上面的步骤。右边的图中黑线就是Jensen不等式构造的下边界函数。
接下来就是公式实现EM算法部分。
首先,列出我们的对数似然函数
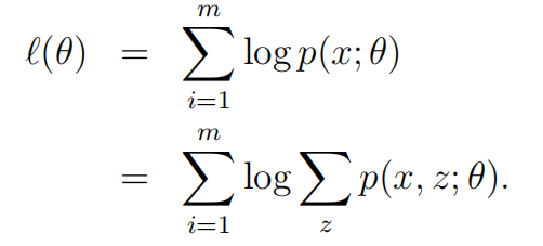
转换成下面这种形式:
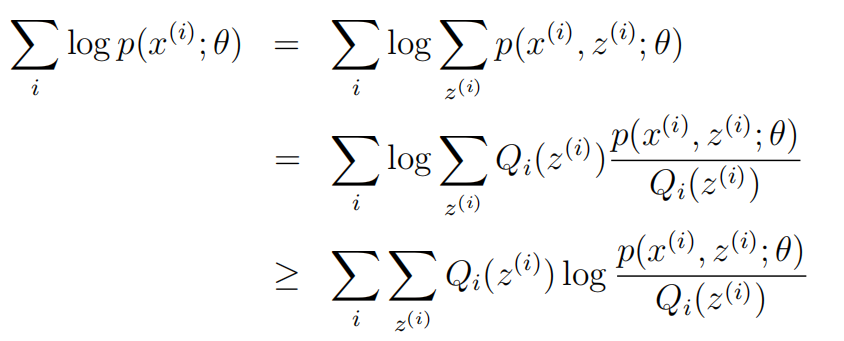
在这里Qi是z的概率分布。 满足条件:![]()
log函数是凹函数,f(EX) ≥ E[f(X)]
在这里X变量是![]()
EX是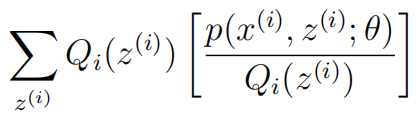
接下来就是E-step和M-step的推导过程:

接下来就是证明似然函数收敛,即证明 ![]() 即可。
即可。
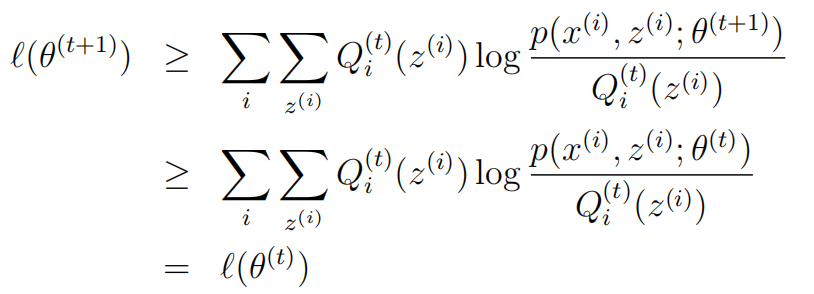
第一个不等式里面Qi的t和P的t+1不同,这是没关系的,因为分子分母都加了一个Qi,可以相互抵消。这一点从
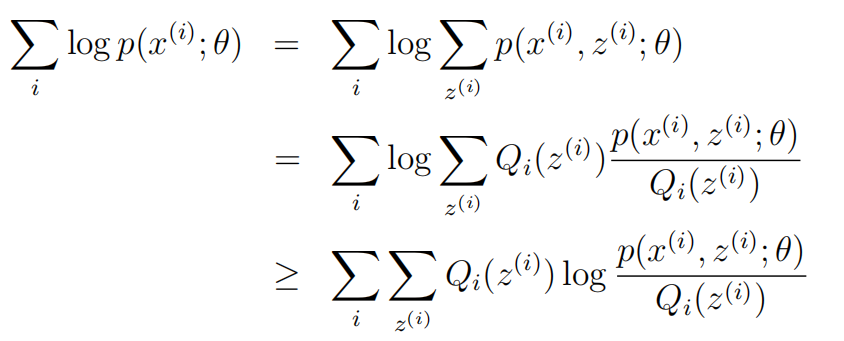 这里面得出来的。
这里面得出来的。
第二个不等式是根据下面这一点得出来的。
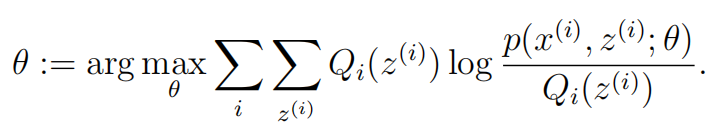
Mixture of Gaussians revisited
在这里,没有介绍混合高斯,建议先学习一下混合高斯再来理解下面的内容。
前面是EM算法的一般形式,现在运用EM算法来解决混合高斯时,EM算法可写成如下形式:
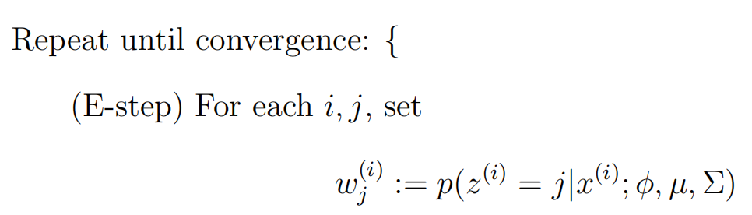

现在回顾一下高斯混合算法,由于含有隐藏变量,无法像高斯判别分析一样解决,由此我们借助EM算法。
一般形式的EM算法E步输出:![]()
高斯混合的EM算法E步输出:![]()
所以在M步需要最大化的下边界J变成了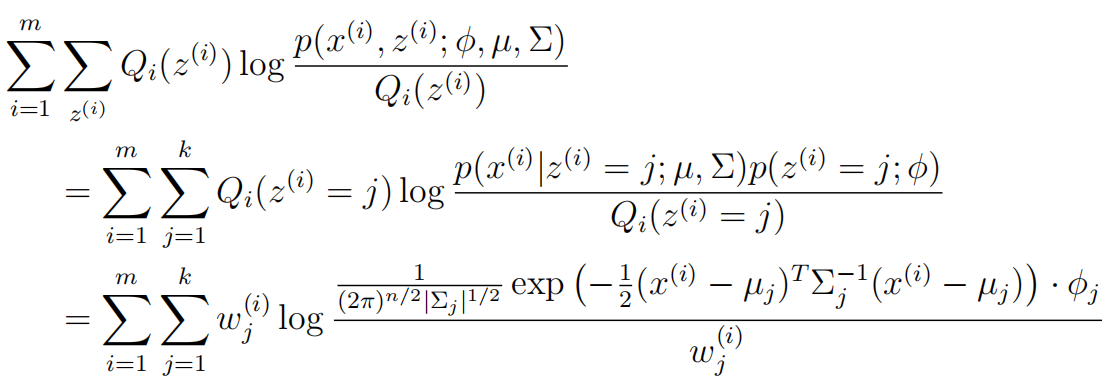
第三个等式的由来:

已经得到需要最大化的下边界,接下来就是进行参数的更新。一般的EM算法只需要更新参数θ,在这里我们需要更新三个参数: φ, µ, Σ。

