查找

顺序查找

　　顺序查找是指将序列从头开始遍历，直到找到指定的元素为止。

　　在一个元素为n的序列中查找不存在的元素，需要比较n次。顺序查找虽然效率低下，但是却适用于任何序列。

　　顺序查找的代码如下：

public static int seqSearch(int[] arr, int val) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == val) return i;
    }
    return -1;
}

　　例如，在序列（1, 2, 3, 4, 5, 6, 7, 8, 9）中查找元素7：从1开始比较，直到找到了7所在位标并返回。

　　顺序查找一共比较了7次。

二分查找

　　二分查找是指取有序序列中间的元素作为枢轴，枢轴两边被分割为两个子序列，一边比枢轴大，另一边比枢轴小。这样，查找的元素要么为枢轴，要么在其中一个子序列中。每次递归查找时，可以将区间规模大致缩减一半，从而大大加快查找效率。

　　在一个元素为n的序列中查找不存在的元素，需要比较log₂n次。二分查找只适用于有序序列。

　　二分查找的代码如下：

public static int binarySearch(int[] arr, int low, int high, int val) {
    if (low > high) return -1;
    int mid = (low + high) / 2;
    if (arr[mid] == val) return mid;
    if (arr[mid] > val)   // 降序则为arr[mid] < val
        return binarySearch(arr, low, mid - 1, val);
    return binarySearch(arr, mid + 1, high, val);
}

　　例如，在序列（1, 2, 3, 4, 5, 6, 7, 8, 9）中查找元素7：

　　　　a. 找到序列最中间的元素5，5 < 7，需要对右子序列递归查找。

　　　　b. 找到右子序列最中间的元素7，7 = 7，找到元素。

　　二分查找一共比较了2次。

插值查找

　　插值查找与二分查找类似。二分查找是以序列中间的元素作为枢轴，即

　　　　

　　而插值查找获取枢轴的公式为：

　　　　

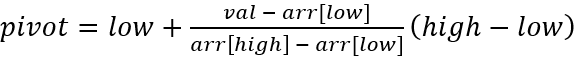
　　其中，low和high分别是当前序列第一个元素的位标和最后一个元素的位标。

　　与二分查找一样，插值查找只适用于有序序列。有序序列越接近等差序列，插值查找的效率越高。

　　插值查找的代码如下：

public static int insertValueSearch(int[] arr, int low, int high, int val) {
    // arr[low] > val和arr[high] < val是为了防止val数值过大，导致算出的mid越界
    if (low > high || arr[low] > val || arr[high] < val) return -1;
    int mid = low + (high - low) * (val - arr[low]) / (arr[high] - arr[low]);
    if (arr[mid] == val) return mid;
    if (arr[mid] > val)   // 降序则为arr[mid] < val
        return insertValueSearch(arr, low, mid - 1, val);
    return insertValueSearch(arr, mid + 1, high, val);
}

　　例如，在序列（1, 2, 3, 4, 5, 6, 7, 8, 9）中查找元素7：直接代入计算枢轴的值为pivot = 0 + [(7 - 1) / (9 - 1)] * (8 - 0) = 6，而arr[6] = 7。

　　插值查找一共比较了1次。

斐波那契查找

　　斐波那契数列的特点为：f(n) = f(n - 1) + f(n - 2)。将该式变化后得到：f(n) - 1 = [f(n - 1) - 1] + [f(n - 2) - 1] + 1。

　　斐波那契查找也与二分查找类似，其获取枢轴的公式为：

　　　　

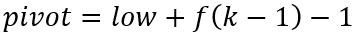
　　也就是说，枢轴将有序序列分割为：

　　　　

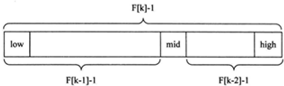
　　斐波那契查找只适用于有序序列，而且在查找前需要保证序列长度为f(k) - 1（如果长度不为f(k) - 1则需要扩容，其扩容的空间使用原序列最后一个元素填充）。

　　斐波那契查找的代码如下：

public static int fibonacciSearch(int[] arr, int val) {
    int low = 0, high = arr.length - 1, mid;
    // 找到第一个满足f(k) - 1 >= arr.length的k
    int k = 1;
    while (f.get(k) - 1 < arr.length) k++;
    // 扩容
    int[] temp = Arrays.copyOf(arr, f.get(k) - 1);
    for (int i = arr.length; i < temp.length; i++) temp[i] = arr[arr.length - 1];
    while (low <= high) {
        mid = low + f.get(k - 1) - 1;
        if (val < temp[mid]) {   // 降序则为val > temp[mid]
            high = mid - 1;
            k--;
        } else if (val > temp[mid]) {   // 降序则为val < temp[mid]
            low = mid + 1;
            k -= 2;
        } else {
            if (mid <= high) return mid;
            return high;
        }
    }
    return -1;
}

　　例如，在序列（1, 2, 3, 4, 5, 6, 7, 8, 9）中查找元素7：

　　　　a. 原序列长度为9 < f(6) - 1 = 12，所以需要扩容到长度为12，且使用元素9填充，序列变为（1, 2, 3, 4, 5, 6, 7, 8, 9, 9, 9, 9）。此时，k = 6。

　　　　b. 枢轴pivot = 0 + f(6 - 1) - 1 = 7，arr[pivot] =  8 > 7，所以7位于左子序列（0, 6）中。此时，k = 5。

　　　　c. 枢轴pivot = 0 + f(5 - 1) - 1 = 4，arr[pivot] = 5 < 7，所以7位于右子序列（5, 6）中。此时，k = 3。

　　　　d. 枢轴pivot = 5 + f(3 - 1) - 1 = 6，arr[pivot] = 7，找到指定元素的位标。

　　斐波那契查找一共比较了3次。