Codeforces Round #644 (Div. 3) D. Buying Shovels (数学)

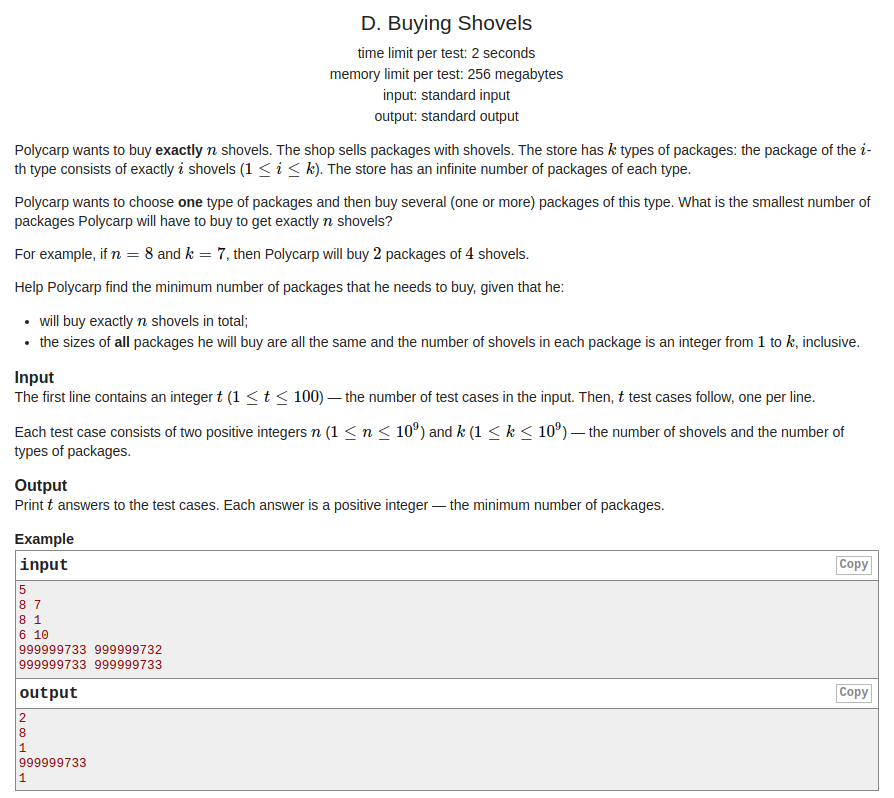
• 题意:商店里有\(k\)个包裹,第\(i\)个包裹中含有\(i\)个物品,现在想要买\(n\)物品,你可以选择某一个包裹购买任意次,使得物品数刚好等于\(n\),求最少的购买次数.

• 题解:首先,假如\(k\ge n\),那么只用买一次.否则,我们枚举\(1\)~\(\sqrt n\),若\(n\ mod\ i=0\):

  ​ 1.\(n/i\le k\),那么\(i\)一定是我们所需要的最小购买次数,

  ​ 2.\(n/i>k\),只要\(i\le k\),我们就维护\(ans\)和\(n/i\)的最小值.

  ​ 纸上谈来终觉浅,要自己去好好思考,对数字敏感一点,也就想出来了.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
   
  int t;
  ll n,k;
   
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
      cin>>t;
       while(t--){
           cin>>n>>k;
           if(n<=k){
               printf("1\n");
           }
           else{
               bool ok=0;
               ll ans=INF;
               for(ll i=1;i*i<=n;++i){
                   if(n%i==0){
                       if(n/i<=k){
                           ok=1;
                           ans=i;
                           break;
                       }
                       else{
                           if(i<=k){
                               ans=min(ans,n/i);
                           }
                       }
                   }
               }
               printf("%lld\n",ans);
           }
   
       }
   
      return 0;
  }