[Luogu1436]棋盘分割（动态规划）

[Luogu1436]棋盘分割

题目背景

无

题目描述

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

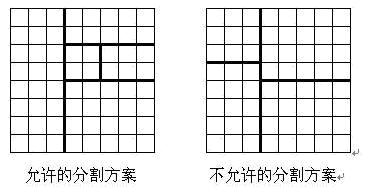
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

输入输出格式

输入格式：

第1行为一个整数n(1 < n < 15)。

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式：

仅一个数，为平方和。

输入输出样例

输入样例#1：

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例#1：

1460

最开始被告知这道题是区间dp，做完之后发现好像并没什么太大的关系，直接枚举就可以了。
(F[i][x1][y1][x2][y2])表示矩形((x1,y1),(x2y2))分成了i块后，获得的最大值。这里注意不能枚举矩阵中的小矩阵来转移，这样有可能会切重。所以我们直接枚举长和宽的断点来转移即可。
注意初始状态。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*w;
}
int n;
int a[15][15],sum[15][15];
int dp[16][11][11][11][11];
int get(int x1,int y1,int x2,int y2,int x3,int y3)
{
    int d=(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]-sum[x3][y3]+sum[x3][y1-1]+sum[x1-1][y3]);
    return d*d;
}
void init()
{
    for(int x1=1;x1<=8;x1++)
    {
        for(int y1=1;y1<=8;y1++)
        {
            for(int x2=x1;x2<=8;x2++)
            {
                for(int y2=y1;y2<=8;y2++)
                {
                    int d=(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]);
                    dp[1][x1][y1][x2][y2]=d*d;
                }
            }
        }
    }
    
}
int main()
{
    memset(dp,0x3f,sizeof(dp));
    n=read();
    for(int i=1;i<=8;i++)
    {
        for(int j=1;j<=8;j++)
        {
            a[i][j]=read();
            sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
        }
    }
    init();
    for(int i=2;i<=n;i++)
    {
        for(int x1=1;x1<=8;x1++)
        {
            for(int y1=1;y1<=8;y1++)
            {
                for(int x2=x1;x2<=8;x2++)
                {
                    for(int y2=y1;y2<=8;y2++)
                    {
                        for(int x3=x1;x3<x2;x3++)
                        dp[i][x1][y1][x2][y2]=min(dp[i][x1][y1][x2][y2],min(dp[i-1][x1][y1][x3][y2]+dp[1][x3+1][y1][x2][y2],dp[1][x1][y1][x3][y2]+dp[i-1][x3+1][y1][x2][y2]));
                        for(int y3=y1;y3<y2;y3++)
                        dp[i][x1][y1][x2][y2]=min(dp[i][x1][y1][x2][y2],min(dp[i-1][x1][y1][x2][y3]+dp[1][x1][y3+1][x2][y2],dp[1][x1][y1][x2][y3]+dp[i-1][x1][y3+1][x2][y2]));
                    }
                }
            }
        }
    }
    cout<<dp[n][1][1][8][8];
}