[思维构造] 题解 Robot Arms

[思维构造] 题解 Robot Arms

题目链接

题目分析

好吧，这道题目按理来说应该是套路题，但是我就是不会，所以写篇题解学习一下。

首先如果 (X_i+Y_i) 的奇偶性不同就无解，因为每次操作后 (X_i+Y_i) 的奇偶性都是固定的，不肯能出现奇偶性不同的情况。

如果 (X_i+Y_i) 的奇偶性全部相同，那么必定有解，当 (X_i+Y_i) 为偶数的时候可以通过一次走动变成奇数，所以只考虑 (X_i+Y_i) 为奇数的情况。

可以使用二进制来构造，通过序列 (1,2,4,8,16,dots,2^k) 可以从 ((0,0)) 走到任意一个满足 (mbox{abs}(x)+mbox{abs}(y)<2^{k+1}) 并且 (x+y) 为奇数的位置 ((x,y)) ，可以使用归纳法来证明。

(k=0) 时，显然序列 (1) 可以到达 ((1,0),(0,1),(-1,0),(0,-1)) 。

假设 (1,2,4,dots,2^{k-1}) 满足该条件，然后我们新加入了一个数 (2^k) ，如果 ((x,y)) 满足 (mbox{abs}(x)+mbox{abs}(y)<2^{k+1}) 并且 (x+y) 为奇数，那么 (mbox{abs}(x)) 和 (mbox{abs}(y)) 中最多只有一个数的二进制第 (k) 位为 (1) ，不妨假设 (mbox{abs}(x)>mbox{abs}(y)) （需要注意 (mbox{abs}(x) e mbox{abs}(y)) ，否则不满足 (mbox{abs}(x)+mbox{abs}(y)) 是奇数），如果 (mbox{abs}(x)ge 2^k) ，那么我们可以令 (mbox{abs}(x)) 变成 (mbox{abs}(x)-2^k) ，仍然满足条件，否则我们可以令 (mbox{abs}(x)) 变成 (2^k-mbox{abs}(x)) ，则 (2^k-mbox{abs}(x)+mbox{abs}(y)<2^k) ，仍然满足条件。

当然也可以通过图来理解，每次序列增加一个数相当于是覆盖的点向上向下向左向右并起来的所有点：

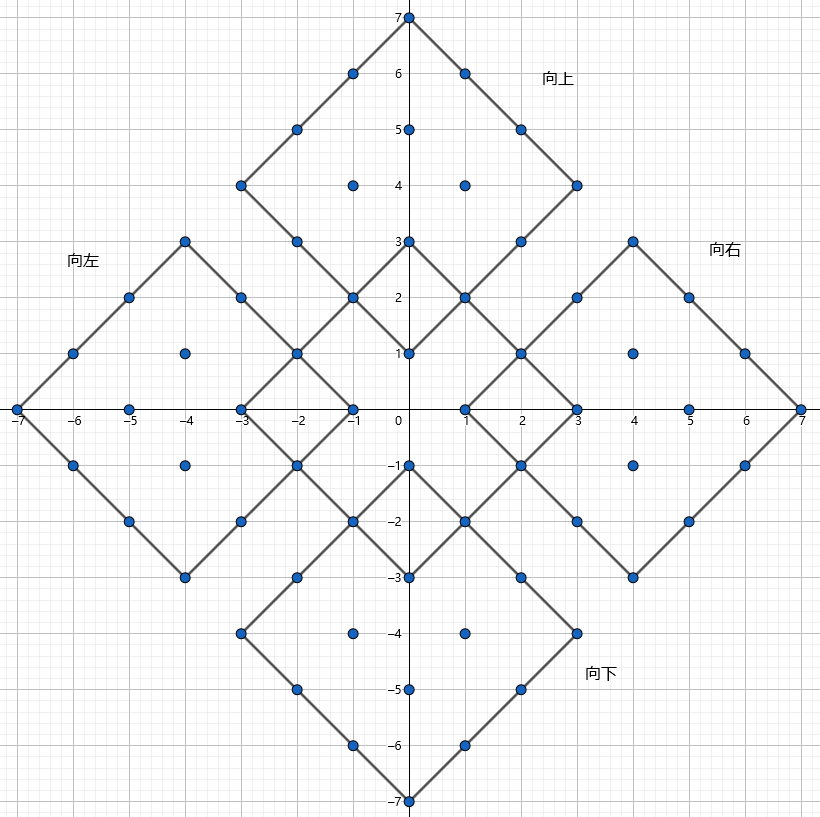
不难发现，从 ((0,0)) 通过序列 (1,2,4,8,dots,2^k) 只有唯一的方法走到 ((x,y)) ，直接递归求解即可。

参考代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=1005,Base=38;
long long _[Base];
long long ABS(long long x){
	return x<0?-x:x;
}
int judge(long long x,long long y,int sp){
	return ABS(x)+ABS(y)<_[sp+1];
}
void solve(long long x,long long y,int sp){
	if(~sp){
		if(judge(x-_[sp],y,sp-1)){solve(x-_[sp],y,sp-1);pc('R');}
		if(judge(x+_[sp],y,sp-1)){solve(x+_[sp],y,sp-1);pc('L');}
		if(judge(x,y-_[sp],sp-1)){solve(x,y-_[sp],sp-1);pc('U');}
		if(judge(x,y+_[sp],sp-1)){solve(x,y+_[sp],sp-1);pc('D');}
	}
}
long long X[maxn],Y[maxn];
int main(){
	int n,s=0,ok=true;read(n);
	for(int i=1;i<=n;++i){
		read(X[i]),read(Y[i]);
		if(i==1)s=(X[i]+Y[i])&1;
		else ok&=(s==((X[i]+Y[i])&1));
	}
	if(!ok)puts("-1");
	else{
		_[0]=1;
		for(int i=1;i<Base;++i)
			_[i]=_[i-1]<<1;
		if(s&1)write(Base),pc('
');
		else   write(Base+1),pc('
'),write(1),pc(' ');
		for(int i=0;i<Base;++i)write(_[i]),pc(" 
"[i==Base-1]);
		for(int i=1;i<=n;++i){
			if(!((X[i]+Y[i])&1))pc('L'),++X[i];
			solve(X[i],Y[i],Base-1);pc('
');
		}
	}
	return 0;
}