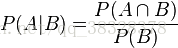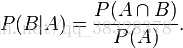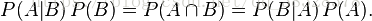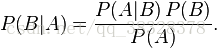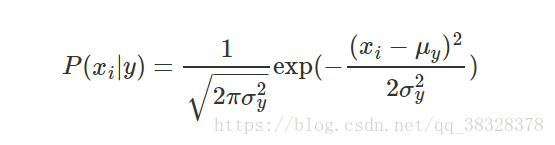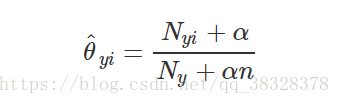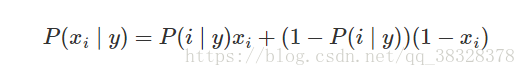朴素贝叶斯算法 -- 简介
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model,NBM)。
和决策树模型相比,朴素贝叶斯分类器(Naive Bayes Classifier,或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。
理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。
朴素贝叶斯算法 -- 步骤
算法步骤:
1)收集数据;
2)准备数据:需要数值型或布尔型数据。如果是文本文件,要解析成词条向量bai;
3)分析数据:有大量特征时,用直方图分析效果更好;
4)训练算法:计算不同的独立特征的条件概率;
5)测试算法:计算错误率;
6)使用算法:一个常见的朴素贝叶斯应用是文档分类。
贝叶斯定理
条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在 B 发生的条件下 A 发生的概率”。
联合概率表示两个事件共同发生(数学概念上的交集)的概率。A 与 B 的联合概率表示为 。
。
推导
我们可以从条件概率的定义推导出贝叶斯定理。
根据条件概率的定义,在事件 B 发生的条件下事件 A 发生的概率为:
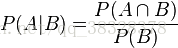
同样地,在事件 A 发生的条件下事件 B 发生的概率为:
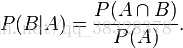
结合这两个方程式,我们可以得到:
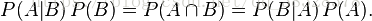
这个引理有时称作概率乘法规则。上式两边同除以 P(A),若P(A)是非零的,我们可以得到贝叶斯定理:
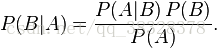
高斯朴素贝叶斯(GaussianNB)
在高斯朴素贝叶斯中,每个特征都是连续的,并且都呈高斯分布。高斯分布又称为正态分布。图画出来以后像一个倒挂的钟,以均值为轴对称,如下图所示:
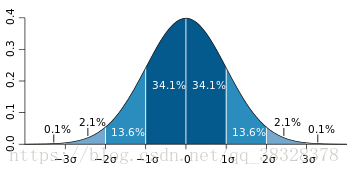
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:
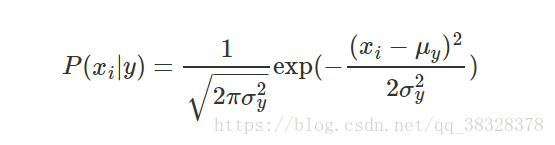
参数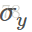 和
和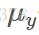 使用最大似然法估计。
使用最大似然法估计。
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf = clf.fit(iris.data, iris.target)
y_pred=clf.predict(iris.data)
print("高斯朴素贝叶斯,样本总数: %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))
多项分布朴素贝叶斯(MultinomialNB)
MultinomialNB实现服从多项分布数据(multinomially)的贝叶斯算法,是一个经典的朴素贝叶斯文本分类中使用的变种(其中的数据是通常表示为词向量的数量,虽然TF-IDF向量在实际项目中表现得很好),对于每一个y来说,分布通过向量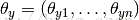 参数化,n是类别的数目(在文本分类中,表示词汇量的长度)
参数化,n是类别的数目(在文本分类中,表示词汇量的长度) 表示标签i出现的样本属于类别y的概率
表示标签i出现的样本属于类别y的概率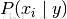 。
。
该参数  是一个平滑的最大似然估计,即相对频率计数:
是一个平滑的最大似然估计,即相对频率计数:
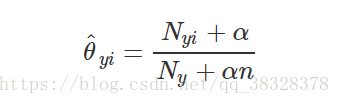
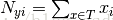 表示标签i在样本集T中属于类别y的 数目
表示标签i在样本集T中属于类别y的 数目
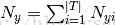 表示在所有标签中类别y出现的数目
表示在所有标签中类别y出现的数目
先验平滑先验 α >=0表示学习样本中不存在的特征并防止在计算中概率为0,设置 α = 1被称为拉普拉斯平滑(Lapalce smoothing),当α<1称为利德斯通平滑(Lidstone smoothing)
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB()
clf = clf.fit(iris.data, iris.target)
y_pred=clf.predict(iris.data)
print("多项分布朴素贝叶斯,样本总数: %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))
参数说明如下:
alpha:浮点型可选参数,默认为1.0,其实就是添加拉普拉斯平滑,即为上述公式中的λ ,如果这个参数设置为0,就是不添加平滑;
fit_prior:布尔型可选参数,默认为True。布尔参数fit_prior表示是否要考虑先验概率,如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量,mk为输出为第k类别的训练集样本数。
class_prior:可选参数,默认为None。
总结如下:
fit_prior class_prior 最终先验概率
False 填或不填没有意义 P(Y = Ck) = 1 / k
True 不填 P(Y = Ck) = mk / m
True 填 P(Y = Ck) = class_prior
伯努利朴素贝叶斯(BernoulliNB)
BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法,即有多个特征,但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此,这类算法要求样本以二元值特征向量表示;如果样本含有其他类型的数据, 一个 BernoulliNB 实例会将其二值化(取决于 binarize 参数)。
伯努利朴素贝叶斯的决策规则基于:
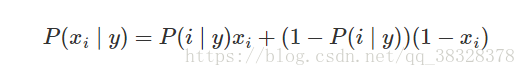
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ,而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
在文本分类的例子中,词频向量(word occurrence vectors)(而非词数向量(word count vectors))可能用于训练和用于这个分类器。 BernoulliNB 可能在一些数据集上可能表现得更好,特别是那些更短的文档。 如果时间允许,建议对两个模型都进行评估。
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf = clf.fit(iris.data, iris.target)
y_pred=clf.predict(iris.data)
print("伯努利朴素贝叶斯,样本总数: %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))
朴素贝叶斯 -- 代码实现
对于新闻分类,属于多分类问题。我们可以使用MultinamialNB()完成我们的新闻分类问题。
import numpy as np
"""
这个指南的目的是在一个实际任务上探索scikit-learn的主要工具,在二十个不同的主题上分析一个文本集合。
在这一节中,可以看到:
1、加载文本文件和类别
2、适合机器学习的特征向量提取
3、训练线性模型进行分类
4、使用网格搜索策略,找到一个很好的配置的特征提取组件和分类器
"""
"""
1、Loading the 20 newsgroups dataset 加载20个新闻组数据集
为了获得更快的执行时间为第一个例子,我们将工作在部分数据集只有4个类别的数据集中:
"""
categories = ['alt.atheism', 'soc.religion.christian', 'comp.graphics', 'sci.med']
from sklearn.datasets import fetch_20newsgroups
twenty_train = fetch_20newsgroups(subset='train', categories=categories, shuffle=True, random_state=42)
print(twenty_train.target)
print(twenty_train.target_names) # 训练集中类别的名字,这里只有四个类别
print(len(twenty_train.data)) # 训练集中数据的长度
print(len(twenty_train.filenames)) # 训练集文件名长度
print('-----')
print("
".join(twenty_train.data[0].split("
")[:3]))
print('-----')
print(twenty_train.target_names[twenty_train.target[0]])
print('-----')
print(twenty_train.target[:10]) # 前十个的类别
print('-----')
for t in twenty_train.target[:10]:
print(twenty_train.target_names[t]) # 类别的名字
print('-----')
"""
2、Extracting features from text files 从文本文件中提取特征
为了在文本文件中使用机器学习算法,首先需要将文本内容转换为数值特征向量
"""
"""
Bags of words 词袋
最直接的方式就是词袋表示法
1、为训练集的任何文档中的每个单词分配一个固定的整数ID(例如通过从字典到整型索引建立字典)
2、对于每个文档,计算每个词出现的次数,并存储到X[i,j]中。
词袋表示:n_features 是语料中不同单词的数量,这个数量通常大于100000.
如果 n_samples == 10000,存储X的数组就需要10000*10000*4byte=4GB,这么大的存储在今天的计算机上是不可能实现的。
幸运的是,X中的大多数值都是0,基于这种原因,我们说词袋是典型的高维稀疏数据集,我们可以只存储那些非0的特征向量。
scipy.sparse 矩阵就是这种数据结构,而scikit-learn内置了这种数据结构。
"""
"""
Tokenizing text with scikit-learn 使用scikit-learn标记文本
文本处理、分词、过滤停用词都在这些高级组件中,能够建立特征字典并将文档转换成特征向量。
"""
from sklearn.feature_extraction.text import CountVectorizer # sklearn中的文本特征提取组件中,导入特征向量计数函数
count_vect = CountVectorizer() # 特征向量计数函数
X_train_counts = count_vect.fit_transform(twenty_train.data) # 对文本进行特征向量处理
print(X_train_counts) # 特征向量和特征标签
print(X_train_counts.shape) # 形状
print('-----')
"""
CountVectorizer支持计算单词或序列的N-grams,一旦合适,这个向量化就可以建立特征词典。
在整个训练预料中,词汇中的词汇索引值与其频率有关。
"""
print(count_vect.vocabulary_.get(u'algorithm'))
print('-----')
"""
From occurrences to frequencies 从事件到频率
计数是一个好的开始,但是也存在一个问题:较长的文本将会比较短的文本有很高的平均计数值,即使他们所表示的话题是一样的。
为了避免潜在的差异,它可以将文档中的每个单词出现的次数在文档的总字数的比例:这个新的特征叫做词频:tf
tf-idf:词频-逆文档频率
"""
from sklearn.feature_extraction.text import TfidfTransformer # sklearn中的文本特征提取组件中,导入词频统计函数
tf_transformer = TfidfTransformer(use_idf=False).fit(X_train_counts) # 建立词频统计函数,注意这里idf=False
print(tf_transformer) # 输出函数属性 TfidfTransformer(norm=u'l2', smooth_idf=True, sublinear_tf=False, use_idf=False)
print('-----')
X_train_tf = tf_transformer.transform(X_train_counts) # 使用函数对文本文档进行tf-idf频率计算
print(X_train_tf)
print('-----')
print(X_train_tf.shape)
print('-----')
"""
在上面的例子中,使用fit()方法来构建基于数据的预测器,然后使用transform()方法来将计数矩阵用tf-idf表示。
这两个步骤可以通过跳过冗余处理,来更快的达到相同的最终结果。
这些可以通过使用fit_transform()方法来实现:
"""
tfidf_transformer = TfidfTransformer() # 这里使用的是tf-idf
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)
print(X_train_tfidf)
print(X_train_tfidf.shape)
print('-----')
"""
Training a classifier 训练一个分类器
既然已经有了特征,就可以训练分类器来试图预测一个帖子的类别,先使用贝叶斯分类器,贝叶斯分类器提供了一个良好的基线来完成这个任务。
scikit-learn中包括这个分类器的许多变量,最适合进行单词计数的是多项式变量。
"""
from sklearn.naive_bayes import MultinomialNB # 使用sklearn中的贝叶斯分类器,并且加载贝叶斯分类器
# 中的MultinomialNB多项式函数
clf = MultinomialNB() # 加载多项式函数
x_clf = clf.fit(X_train_tfidf, twenty_train.target) # 构造基于数据的分类器
print(x_clf) # 分类器属性:MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
print('-----')
"""
为了预测输入的新的文档,我们需要使用与前面相同的特征提取链进行提取特征。
不同的是,在转换中,使用transform来代替fit_transform,因为训练集已经构造了分类器
"""
docs_new = ['God is love', 'OpenGL on the GPU is fast'] # 文档
X_new_counts = count_vect.transform(docs_new) # 构建文档计数
X_new_tfidf = tfidf_transformer.transform(X_new_counts) # 构建文档tfidf
predicted = clf.predict(X_new_tfidf) # 预测文档
print(predicted) # 预测类别 [3 1],一个属于3类,一个属于1类
for doc, category in zip(docs_new, predicted):
print('%r => %s' % (doc, twenty_train.target_names[category])) # 将文档和类别名字对应起来
print('-----')
"""
Building a pipeline 建立管道
为了使向量转换更加简单(vectorizer => transformer => classifier),scikit-learn提供了pipeline类来表示为一个复合分类器
"""
from sklearn.pipeline import Pipeline
text_clf = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()), ('clf', MultinomialNB())])
text_clf = text_clf.fit(twenty_train.data, twenty_train.target)
print(text_clf) # 构造分类器,分类器的属性
predicted = text_clf.predict(docs_new) # 预测新文档
print(predicted) # 获取预测值
print('-----')
"""
分析总结:
1、加载数据集,主要是加载训练集,用于对数据进行训练
2、文本特征提取:
对文本进行计数统计 CountVectorizer
词频统计 TfidfTransformer (先计算tf,再计算tfidf)
3、训练分类器:
贝叶斯多项式训练器 MultinomialNB
4、预测文档:
通过构造的训练器进行构造分类器,来进行文档的预测
5、最简单的方式:
通过使用pipeline管道形式,来讲上述所有功能通过管道来一步实现,更加简单的就可以进行预测
"""
"""
Evaluation of the performance on the test set 测试集性能评价
评估模型的预测精度同样容易:
"""
import numpy as np
twenty_test = fetch_20newsgroups(subset='test', categories=categories, shuffle=True, random_state=42)
docs_test = twenty_test.data
predicted = text_clf.predict(docs_test)
print(np.mean(predicted == twenty_test.target)) # 预测的值和测试值的比例,mean就是比例函数
print('-----') # 精度已经为0.834886817577
"""
精度已经实现了83.4%,那么使用支持向量机(SVM)是否能够做的更好呢,支持向量机(SVM)被广泛认为是最好的文本分类算法之一。
尽管,SVM经常比贝叶斯要慢一些。
我们可以改变学习方式,使用管道来实现分类:
"""
from sklearn.linear_model import SGDClassifier
text_clf = Pipeline(
[('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),
('clf', SGDClassifier(loss='hinge', penalty='l2', alpha=1e-3, n_iter=5, random_state=42))])
# _ = text_clf.fit(twenty_train.data, twenty_train.target) # 和下面一句的意思一样,一个杠,表示本身
text_clf = text_clf.fit(twenty_train.data, twenty_train.target)
predicted = text_clf.predict(docs_test)
print(np.mean(predicted == twenty_test.target)) # 精度 0.912782956059
print('-----')
"""
sklearn进一步提供了结果的更详细的性能分析工具:
"""
from sklearn import metrics
print(metrics.classification_report(twenty_test.target, predicted, target_names=twenty_test.target_names))
print(metrics.confusion_matrix(twenty_test.target, predicted))
 。
。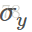 和
和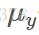 使用最大似然法估计。
使用最大似然法估计。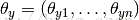 参数化,n是类别的数目(在文本分类中,表示词汇量的长度)
参数化,n是类别的数目(在文本分类中,表示词汇量的长度) 表示标签i出现的样本属于类别y的概率
表示标签i出现的样本属于类别y的概率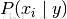 。
。 是一个平滑的最大似然估计,即相对频率计数:
是一个平滑的最大似然估计,即相对频率计数: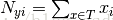 表示标签i在样本集T中属于类别y的 数目
表示标签i在样本集T中属于类别y的 数目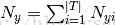 表示在所有标签中类别y出现的数目
表示在所有标签中类别y出现的数目