20190824

一.友好的生物

我去看了神仙陈启峰2016的论文

1.首先我们假设K=3，并且忽略

"但是属性K与众不同，这种属性差别越小的两种生物越友好"这一条件

那么对于任意a,b

那么 (±a.k[1]±a.k[2]±a.k[3])-(±b.k[1]±b.k[2]±b.k[3])

因为根据常理 c-d<=|c-d|

也就是说只有在符号正确的情况下，我们才能得到最大差值

在2^k的枚举下前后同号

如何优化？

假设我们从左向右依次枚举，得到当前最小值Min，那么后面减Min一定更优

2.因为属性K与众不同，这种属性差别越小的两种生物越友好

那么我们按K从小到大排序，以来保证K的属性差别越小

或者说，我们保证后面的值减前面的值总为正

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i) 
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=100005;

int n,m,C[6];
struct node
{
    int k[6];
    bool operator<(node b)const 
    {
        re k[m]<b.k[m];
    }
}a[maxn];


int main()
{
    
    rd(n),rd(m);
    inc(i,1,m)rd(C[i]);
    
    inc(i,1,n)
    inc(j,1,m)
    {
        rd(a[i].k[j]);
        a[i].k[j]*=C[j]; 
    }
    
    
    sort(a+1,a+n+1);
    
    int S=1<<(m-1),ans=0,Min;
    
    inc(s,0,S)
    {
        Min=10000000;
        inc(i,1,n)
        {
            int now=0;
            inc(j,1,m-1)
            if(s&(1<<(j-1)))
                now+=a[i].k[j];
            else now-=a[i].k[j];
            now-=a[i].k[m];
            ans=max(ans,now-Min);
            Min=min(Min,now);
        }
    }
    
    printf("%d",ans);
    re 0;
} 

二.基因重组

Juicepry®是一个世界著名的实验室。目前，实验室的科学家们正致力于对生物基因的重组进行深入研究。基因的物质载体是脱氧核糖核酸（DNA）。DNA是一种仅由A、T、G、C四种基元构成的双螺旋结构的有机分子。
DNA的两条单链上，同一位置的两个基元是互相对应的。A对T，G对C，因此，我们只需用任意一条链上的基元排列，就可以表示DNA的分子结构。例如：ATTGAGCCGTAT。
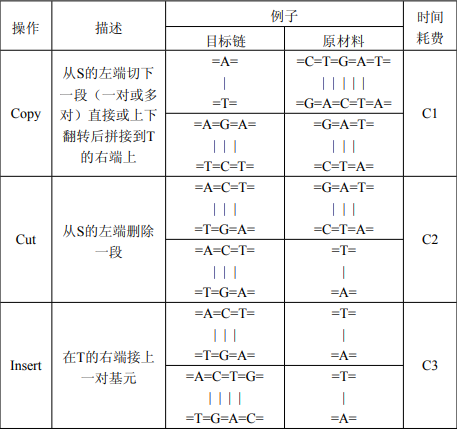
由于DNA微小而复杂，重组DNA极其困难，科学家们打算利用一条现成的DNA链作原材料拼接成另外一条新的DNA链。即使这样，拼接DNA仍然是一件繁重的工作，非人力所能胜任。所以科学家们制造了一种手术机器人TuringM来完成这项任务。TuringM每次只能在目标链(T)的右端与原材料 (S) 的左端进行操作。它有下列几种基本拼接操作：

对于每种操作，机器人的单位时间耗费如上表所示（单位：分钟）。最后剩余的原材料自动丢弃。
现在的任务是请你编一个程序，帮助科学家们找出完成DNA链拼接的最少时间。

可怜八月二十四，LL不会做dp

设f[i][j][k]表示枚举到S的前i，T的前j个，通过第K（0：当前最小值，1：正向copy，2：逆向copy，3：删除）种方式

我们可以推出如下式子

 f[i][j][0]=min(f[i][j][1],f[i][j][2],f[i][j][3],f[i][j-1][0]+c3)

if(s[i]==t[i]) f[i][j][1]=min(f[i-1][j-1][1],f[i-1][j-1][0]+c1)

if(s[i]==match[t[i]]) f[i][j][2]=min(f[i-1][j-1][2],f[i-1][j-1][0]+c1)

f[i][j][3]=min(f[i-1][j][3],f[i-1][j][0]+c2)

 然后卡卡空间，二维滚动

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)

using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=5005;
int n,m,c1,c2,c3,ans=2147483647,f[2][maxn][4];
char s[maxn],ss[maxn],match[100];

int main()
{
    freopen("in.txt","r",stdin);
    
    match['A']='T';match['T']='A';
    match['C']='G';match['G']='C';
    
    scanf("%d%d%d",&c1,&c2,&c3);
    
    scanf("%s%s",s+1,ss+1);
    n=strlen(s+1);m=strlen(ss+1);
    
    memset(f,0x3f3f3f3f,sizeof f);
    
    //除了在一开始都没加的情况下为0
    //其他相当于一直在减 
    f[0][0][0]=0;
    f[1][0][0]=c2;

    
    //预处理出第一个串一个也不用的情况 
    inc(i,1,m)f[0][i][0]=f[0][i-1][0]+c3;
    ans=f[0][m][0];
    for(int num=1,i=1;num<=n;++num,i=1-i)
    {
        
        inc(j,1,m)
        {
            if(s[num]==ss[j])
            f[i][j][1]=min(f[i^1][j-1][1],f[i^1][j-1][0]+c1);
            else f[i][j][1]=0x3f3f3f3f;
        
            if(s[num]==match[ss[j]])
            f[i][j][2]=min(f[i^1][j-1][2],f[i^1][j-1][0]+c1);
            else f[i][j][2]=0x3f3f3f3f;
        
            f[i][j][3]=min(f[i^1][j][3],f[i^1][j][0]+c2); 
        
            f[i][j][0]=min(f[i][j-1][0]+c3,f[i][j][1]);
            f[i][j][0]=min(f[i][j][0],f[i][j][2]);
            f[i][j][0]=min(f[i][j][0],f[i][j][3]); 
        
            if(j==m)
            ans=min(ans,f[i][j][0]);
        }
        f[0][0][0]=f[1][0][0]=c2;
        
    }
    
    printf("%d",ans);
    re 0;
} 

二.危险的迷宫

近来发现了一个古老的地下迷宫，已探明该迷宫是一个A行B列的矩阵，该迷宫有N个不同的出口与N个不同的入口，任一单元格不会既为入口又为出口。为了进一步探明与发掘该迷宫，N个考古队员分别从地上的N个不同的入口进入迷宫，并且计划从N个不同的出口出来。每个队员任意选择一个出口出来，但任意两名队员不会选择同一个出口。
　　迷宫中的每一格与其相邻的某些格相通。该迷宫设计非常精妙，在不知道具体机关的情况下，人一旦离开其所在格后，该格将迅速关闭，且再也不能开启，也就是说每一格仅能进入一次。更糟的是，迷宫中的每一格都有一定的危险性，专家们用1至100的整数表示，数值越大表示越危险。正因为如此，再加之每一格都不很宽敞，两人一起进入比较危险，所以规定不能两个人同时进入同一格。
　　为了队员们的安全着想，希望你能够编程求出如何使队员们所经过单元格的危险性总和最小。
【样例解释】
　　有如下迷宫：
　　每一格中的数字表示该格的危险程度。两格间若有空缺，表示这两格相通。
　　入口有两个：（1，1）即第一行第一列，（1，2）即第一行第二列
　　出口也有两个：（2，3）即第二行第三列，（3，4）即第三行第四列
　　两名队员的最好的行动方案之一，如上图红蓝箭头所示。危险程度之和最小为235。

 莫说了，最小费用最大流模板

#include<bits/stdc++.h>
#define re return
#define ll long long
#define inc(i,l,r) for(int i=l;i<=r;++i)

using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=305;

int n,m,K,V,s,k=1,t,C,hd[maxn];
int cur[maxn],dis[maxn],vis[maxn];

struct node{
    int to,nt,flow,cost;
}e[100000];
inline void add(int x,int y,int flow,int w)
{
    e[++k].to=y;e[k].nt=hd[x];hd[x]=k;e[k].flow=flow;e[k].cost=w;
    e[++k].to=x;e[k].nt=hd[y];hd[y]=k;e[k].flow=0;   e[k].cost=-w;
}

inline bool bfs()
{
    inc(i,1,t)
    dis[i]=214545444;
    
    dis[s]=0;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        vis[u]=0;
        q.pop();
        for(int i=hd[u];i;i=e[i].nt)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].cost&&e[i].flow)
            {
                dis[v]=dis[u]+e[i].cost;
                if(!vis[v])q.push(v);
                vis[v]=1;
            }
        }
    }
    re dis[t]!=214545444;
}


inline int dfs(int u,int flow)
{
    if(u==t)
    {
        C+=flow*dis[t];
        re flow;
    }
    int delta=flow;
    for(int &i=cur[u];i;i=e[i].nt)
    {
        int v=e[i].to;
        if(dis[v]==dis[u]+e[i].cost&&e[i].flow)
        {
            int d=dfs(v,min(delta,e[i].flow));
            e[i].flow-=d;e[i^1].flow+=d;
            delta-=d;
            if(!delta)re flow; 
        }
    }
    re flow-delta;
}

int main()
{

    freopen("maze.in","r",stdin);
    freopen("maze.out","w",stdout);
    
    int x1,x2,y1,y2,x,y;
    rd(n),rd(m);
    int tot=n*m;
    s=tot+tot+1;
    t=s+1;
    inc(i,1,n)
    {
        int v=(i-1)*m;
        inc(j,1,m)
        {
            rd(x);
            add(v+j,v+j+tot,1,x);
        }
    }
    
    rd(K);
    inc(i,1,K)
    {
        rd(x1),rd(y1),rd(x2),rd(y2);
        add((x1-1)*m+y1+tot,(x2-1)*m+y2,1,0);
        add((x2-1)*m+y2+tot,(x1-1)*m+y1,1,0);
    }
    
    rd(V);
    inc(i,1,V)
    {
        rd(x),rd(y);
        add(s,(x-1)*m+y,1,0);
    }
    inc(i,1,V)
    {
        rd(x),rd(y);
        add((x-1)*m+y+tot,t,1,0);
    } 
    
    
    int ans=0;
    while(bfs())
    {
        inc(i,1,t)cur[i]=hd[i];
        ans+=dfs(s,V);
    }
    if(ans==V)
    printf("%d",C);
    else printf("-1");
    re 0;
}