前面介绍了最小生成树和Prim算法,这篇博客继续记录Kruskal算法的相关内容。
算法思想:
1. 先将所有边按权值由小到大排序;
2. 从边集中选出第一条边(即权值最小的边),如果与树中现有的边不构成环,则将其加入树中;
3. 重复步骤2直至树中有n-1条边。
在实现上述算法之前,要先解决三个问题:
1. 如何表示一条边?
虽然我们尽量简化情景方便实现,但是边还是不能像节点一样简单地用一个数表示,因为它有三个必备的属性:起点、终点和权值。因此,我们创建以下结构体来表示边:
1 // 定义表示边的结构体 2 typedef struct Edge 3 { 4 int u; // 起始节点 5 int v; // 终止节点 6 int weight; // 权值 7 };
2. 如何将边按权值排序?
虽然可以用普通的排序方法将边排序,但是移动结构体的时间代价有点大,影响性能;可以考虑使用一个整型数组保存边序列,排序只改变这个数组中元素的指向,类似指针的作用。这是空间换时间的方法。
由于我们只是验证算法,纯属娱乐,因此就直接对结构体排序了。排序方法使用qsort()库函数,为此要定义一个比较函数:
1 int cmpEdge(const void *edge1, const void *edge2) 2 { 3 return ((struct Edge *)edge1)->weight - ((struct Edge *)edge2)->weight; 4 }
3. 如何判断树中的边是否会构成环?
这个问题就有技术含量了,解决方法也很巧妙,使用的是不相交集(Disjoint sets),也叫并查集(Union-find set)。
不相交集(Disjoint sets):从字面上理解,就是每个集合都不相交,没有公共元素;至于为什么又叫并查集,大概是因为这种数据结构的查找(find)和合并(union)操作都比较非主流,所以特意拿出来作为标志吧。
言归正传,不相交集的逻辑结构:所有在同一集合中的元素构成一棵树,互为父子关系。因为每棵树的根是唯一的,所以当要判断两个节点是否在同一集合中时,只要递归地查找出他们的根节点,看是不是同一个就能区分了。而要合并两个集合时,只要将一棵树的根挂到另一棵树的任意一个节点上就行。
应用到Kruskal算法中,是这样的:
1. 用一个数组保存每个节点的父节点信息,初始都为-1表示每个节点都是根节点,也就是有n棵单节点树。我们的目的是要得到一棵有n个节点的树。
2. 每次用上面的算法找到一条边,先判断两端是否在同一棵树中,如果是,则不能再将这条边加到树中,否则会构成环;如果不是,则将一个节点的根挂到另一棵树之下,合成一个集合。至于判断两个节点是不是在同一棵树中的方法,前面已经说了,就看两个节点的根节点是不是一样的。
找出一个节点所在树的根节点很简单:
1 int find(int *parents, int pos) 2 { 3 while (parents[pos] >= 0) 4 { 5 pos = parents[pos]; 6 } 7 8 return pos; 9 }
上面三个问题都已经解决了,下面就可以着手实现Kruskal算法了:

1 int Kruskal(struct Edge *edges, int numEdges, int numNodes) 2 { 3 int *parents; // 保存每个节点的父节点 4 int i, rootU, rootV; 5 int totalWeight = 0; 6 int numFoundEdge = 0; // 已找到边的数量,用于控制循环 7 8 parents = (int *)malloc(numNodes * sizeof(int)); 9 10 // 初始化每个节点的父节点 11 for (i = 0; i < numNodes; ++i) 12 { 13 parents[i] = -1; 14 } 15 16 // 将边集按权值由小到大排序 17 qsort(edges, numEdges, sizeof(struct Edge), cmpEdge); 18 19 // 找出n-1条边 20 printf(" Edge Weight "); 21 i = 0; 22 while (numFoundEdge < numNodes - 1 && i < numEdges) 23 { 24 rootU = find(parents, edges[i].u); 25 rootV = find(parents, edges[i].v); 26 27 // 如果两端点不在同一棵树中 28 if (rootU != rootV) 29 { 30 // 合并两棵树 31 parents[rootU] += parents[rootV]; // 根节点的parent保存树中节点数的相反数 32 parents[rootV] = rootU; // 将rootV挂到rootU之下 33 totalWeight += edges[i].weight; 34 ++numFoundEdge; 35 36 printf("%d->%d %3d ", edges[i].u, edges[i].v, edges[i].weight); 37 } 38 39 ++i; 40 } 41 42 if (numFoundEdge < numNodes - 1) 43 { 44 printf("This is not a connected graph! "); 45 } 46 else 47 { 48 printf(" Total Weight: %d ", totalWeight); 49 } 50 51 return totalWeight; 52 }
再编写一个测试函数:

1 int main() 2 { 3 int i, numNodes, numEdges; 4 struct Edge *edges; 5 6 printf("Num of Nodes and Edges: "); 7 scanf("%d %d", &numNodes, &numEdges); 8 9 edges = (struct Edge *)malloc(numEdges * sizeof(struct Edge)); 10 11 // 输入所有边 12 printf("Input %d Edges: ", numEdges); 13 for (i = 0; i < numEdges; ++i) 14 { 15 scanf("%d %d %d", &edges[i].u, &edges[i].v, &edges[i].weight); 16 } 17 18 Kruskal(edges, numEdges, numNodes); 19 20 return 0; 21 }
同样使用上节的图:
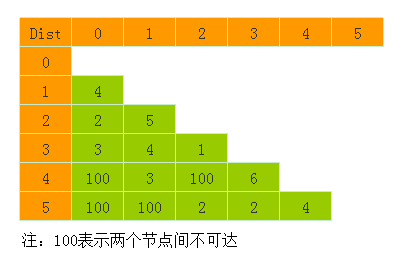
那么应该输入11条边:
0 1 4
0 2 2
0 3 3
1 2 5
1 3 4
1 4 3
2 3 1
2 5 2
3 4 6
3 5 2
4 5 4
程序运行截图:
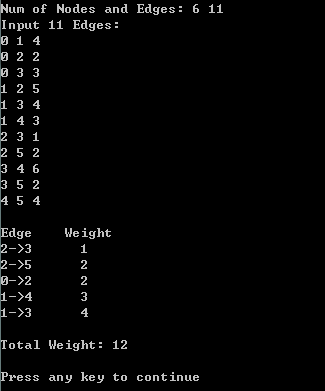
可以看到虽然选出来的边不同,但是总权值是一样的。
再来看一下Kruskal算法的效率:
假设边数为e,使用快排对e条边排序的时间复杂度为O(eloge);e条边执行e次循环,循环内查找根节点的时间复杂度为O(loge);所以总时间复杂度为O(eloge)。
而Prim算法的时间复杂度是O(n^2),n是节点数。比较可以得出以下结论:
Kruskal算法适用于边少的情况,即稀疏图;在边多的情况下,即稠密图中,Prim算法更具优势。
