Liquid Time-constant Networks

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

AAAI 2021

Abstract

　　我们介绍了一类新的时间连续循环神经网络模型。我们不是通过隐式非线性来声明学习系统的动态，而是构造了通过非线性互连门调节的线性一阶动态系统的网络。所得模型表示具有变化的(即液体)时间常数的动态系统，该动态系统耦合到其隐含状态，其输出由数值微分方程求解器计算。这些神经网络表现出稳定且有界的行为，在神经常微分方程族中产生出色的表达性，并提高了时间序列预测任务的性能。为了演示这些特性，我们首先采用一种理论方法来找到它们的动态范围，并通过在潜在轨迹空间中的轨迹长度度量来计算它们的表达能力。然后，我们进行一系列时间序列预测实验，以证明与传统RNN和现代RNN相比，液态时间常数网络(LTC)的近似能力。¹

¹代码和数据可在以下位置获得：https://github.com/raminmh/liquid_time_constant_networks

1 Introduction

　　由常微分方程(ODE)确定的具有连续时间隐含状态的循环神经网络是一种有效的算法，可用于建模广泛用于医疗，工业和商业环境的时间序列数据。神经ODE的状态，由该方程的解定义(Chen et al. 2018)：dx(t)/dt = f(x(t), I(t), t, θ)，并使用由θ参数化的神经网络f。然后可以使用数值ODE求解器计算状态，并通过执行反向模式自动微分(Rumelhart, Hinton, and Williams 1986)，通过求解器的梯度下降(Lechner et al. 2019)或通过将求解器视为黑盒(Chen et al. 2018; Dupont, Doucet, and Teh 2019; Gholami, Keutzer, and Biros 2019)并应用伴随方法(Pontryagin 2018)。开放的问题是：神经ODE在目前的形式中表现力如何，我们能否改善其结构以实现更丰富的表示学习和表现力？

　　与其直接通过神经网络 f 定义隐含状态的导数，不如通过以下公式确定更稳定的连续时间循环神经网络(CT-RNN)(Funahashi and Nakamura 1993)：，其中项协助自治系统达到具有时间常数τ的平衡状态。x(t)是隐含状态，I(t)是输入，t表示时间，f由θ参数化。

　　我们提出一个替代公式：让网络的隐含状态流由以下形式的线性ODE系统声明：dx(t)/dt = -x(t)/τ + S(t)，并令表示由参数θ和A决定的非线性度，S(t) = f(x(t), I(t), t, θ)(A - x(t))。在S插入到隐含状态方程中，我们得到：

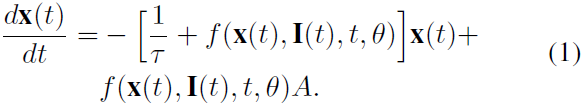
　　等式1展示了一个新颖的时间连续RNN实例，它具有以下功能和优点：

液体时间常数。神经网络 f 不仅确定隐含状态x(t)的导数，而且还用作依赖于输入的可变时间常数(τ_sys = τ / (1 + τ f(x(t), I(t), t, θ))用于学习系统(时间常数是表征ODE的速度和耦合灵敏度的参数)。此属性使隐含状态的单个元素可以识别到达每个时间点的输入特征的专用动态系统。我们将这些模型称为液态时间常数循环神经网络(LTC)。LTC可以通过任意选择ODE求解器来实现。在第2节中，我们介绍了一种实用的固定步长ODE求解器，它同时享受隐式Euler的稳定性和显式Euler方法的计算效率。

LTC的反向模式自动微分。LTC实现可微分的计算图。类似于神经ODE，可以通过基于梯度的优化算法的变量来训练它们。我们通过使用朴素时序反向传播算法来优化LTC而不是基于伴随的优化方法(Pontryagin 2018)，以在反向传递期间以数值精度为代价来交换内存。在第3节中，我们会彻底激发这种选择。

有界的动态-稳定性。在第4节中，我们显示LTC的状态和时间常数被限制在一个有限范围内。此属性确保了输出动态的稳定性，当系统的输入不断增加时，此属性是理想的。

卓越的表现力。在第5节中，我们在理论上和定量上分析了LTC的近似能力。我们采用函数分析方法来显示LTC的普遍性。然后，与其他时间连续模型相比，我们更深入地研究了它们的表达能力。我们通过在潜在轨迹表示中测量网络激活的轨迹长度来执行此操作。引入轨迹长度作为前馈深层神经网络表达能力的量度(Raghu et al. 2017)。我们将这些标准扩展到连续时间循环模型系列。

时间序列建模。在第6节中，我们进行了一系列的11个时间序列预测实验，并将现代RNN的性能与时间连续模型进行了比较。在LTC实现的大多数情况下，我们观察到了性能的改善。

为什么要这样具体表述？选择这种特殊表示法有两个主要依据：

I）LTC模型与小物种中神经动态的计算模型松散地联系在一起，并与突触传递机制结合在一起(Hasani et al. 2020)。非脉冲神经元电位v(t)的动态可以写成线性ODE的形式(Lapicque 1907; Koch and Segev 1998)：dv/dt = g_l v(t) + S(t)，其中S是突触前来源向细胞的所有突触输入的总和，而g_l是泄漏电导。

　　所有进入细胞的突触电流可以通过以下非线性在稳态下近似(Koch and Segev 1998; Wicks, Roehrig, and Rankin 1996)：S(t) = f(v(t), I(t)), (A - v(t))，其中f(·)是sigmoidal非线性，具体取决于所有神经元的状态，当前神经元前突触v(t)以及该细胞的外部输入I(t)。通过插入这两个方程，我们得到了一个类似于公式1的公式，LTC受此基础启发。
II）公式1可能类似于著名的动态因果模型(DCM)(Friston, Harrison and Penny 2003)，其双线性动态系统近似值(Penny, Ghahramani, and Friston 2005)。DCM是通过对动力系统dx/dt = F(x(t), I(t), θ)进行二阶近似(双线性)来制定的，其格式如下(Friston, Harrison, and Penny 2003)：dx/dt = (A + I(t)B)x(t) + C I(t)，其中A = dF/dx，B = dF²/(dx(t)dI(t))，C = dF/dI(t)。DCM和双线性动态系统在学习捕获复杂的fMRI时间序列信号方面显示出了希望。LTC作为连续时间(CT)模型的变体而引入，受到生物学的宽松启发，在对时间序列进行建模时有着出色的表达性，稳定性和性能。

2 LTCs forward-pass by a fused ODE solvers

　　从理论上讲，由于LTC语义的非线性，解公式1是不平凡的。但是，ODE系统的状态在任何时间点T都可以通过数值ODE求解器来计算，该求解器可以模拟从轨迹x(0)到x(T)的系统。ODE求解器将连续的仿真间隔[0, T]分开到离散时间，[t₀, t₁, ... , t_n]。作为结果，求解器的步骤仅涉及将神经元状态从t_i更新为t_i+1。

　　LTC的ODE实现了一个刚性方程组(Press et al. 2007)。当使用基于RungeKutta (RK)的积分器进行仿真时，这种类型的ODE需要指数级的离散化步骤。因此，基于RK的ODE求解器，例如Dormand-Prince (torchdiffeq中的默认值(Chen et al. 2018))不适用于LTC。因此，我们设计了一个新的ODE求解器，它将显式和隐式Euler方法融合在一起(Press et al. 2007)。离散化方法的这种选择导致隐式更新方程的稳定性。为此，Fused求解器通过以下方法以数值形式展开给定动态系统dx/dt = f(x)的形式：

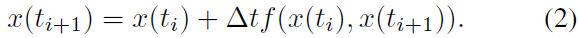
　　特别地，我们仅用x(t_i+1)替换在 f 中线性出现的x(t_i)。作为结果，公式2可以求解x(t_i+1)。将Fused求解器应用于LTC表征，并对其求解x(t + Δt)，我们得到：

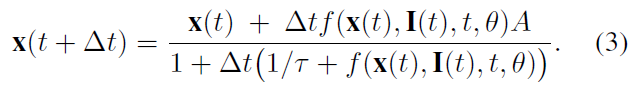
　　公式3为LTC网络计算一个更新状态。相应地，算法1显示了在给定参数空间的情况下如何实现LTC网络。假设 f 具有任意的激活函数(例如，tanh非线性f = tanh(γ_rx + γI + μ))。对于长度为T的输入序列，算法的计算复杂度为O(L x T)，其中L是离散化步骤的数量。直观地讲，具有N个神经元的LTC网络的密集版本和具有N个细胞的长短期记忆(LSTM)网络的密集版本(Hochreiter and Schmidhuber 1997)将具有相同的复杂性。

3 Training LTC networks by BPTT

　　通过应用伴随灵敏度方法执行反向模式自动微分，建议通过神经网络 f 中每一层的常数记忆成本来训练神经ODE(Chen et al. 2018)。然而，伴随方法在反向模式下运行时会出现数值误差。出现这种现象的原因是伴随方法忘记了前向时间计算轨迹，而前向时间计算轨迹在业内被重复表示(Gholami, Keutzer, and Biros 2019; Zhuang et al. 2020)。

　　相反，通过时间的直接反向传播(BPTT)在反向模式积分过程中交换内存以准确恢复前向传播(Zhuang et al. 2020)。因此，我们着手设计一个朴素BPTT算法，以通过求解器保持高度精确的后向传递积分。为此，一个给定的ODE解算器的输出(一个神经状态向量)可以被递归地折叠以建立一个RNN，然后应用算法2中描述的学习算法来训练系统。算法2使用普通的随机梯度下降(SGD)。我们可以用SGD的一个更高性能的变体来代替它，比如Adam (Kingma and Ba 2014)，我们在实验中使用了它。

复杂性。表1总结了与伴随方法相比，我们的朴素BPTT算法的复杂性。我们在前向和后向积分轨迹上都达到了很高的精度，计算复杂度相似，内存开销很大。

4 Bounds on τ and neural state of LTCs

　　LTC由ODE表示，该ODE会根据输入改变其时间常数。因此，重要的是要了解LTC对于无限制的到达输入是否保持稳定(Hasani et al. 2019; Lechner et al. 2020b)。在本节中，我们证明LTC神经元的时间常数和状态被限制在有限范围内，如定理1和定理2所述。

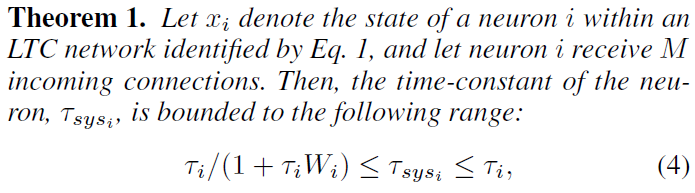
　　该证明在附录中提供。它是基于有界且单调增加的sigmoidal非线性神经网络 f 构造的，并在LTC网络动态中进行了替换。稳定的变化时间常数可以显著增强这种形式的时间连续RNN的表达能力，正如我们在第5节中更正式地发现的那样。

　　证明在附录中给出。它是根据LTC方程的分隔符号以及通过明确的Euler离散化对ODE模型的近似构造而成的。定理2阐明了LTC的理想特性，即状态稳定性，保证了LTC的输出即使输入增加到无穷也不会爆炸。接下来，我们将与时间连续模型(例如CT-RNN和神经常微分方程)系列相比，讨论LTC的表达能力(Chen et al. 2018; Rubanova, Chen, and Duvenaud 2019)。

 

5 On the expressive power of LTCs

　　理解神经网络的结构特性如何确定它们可以计算的功能称为表达性问题。测量神经网络表达能力的早期尝试包括基于功能分析的理论研究。他们表明，具有三层的神经网络可以以任何精度近似任何连续映射的有限集。这就是所谓的通用近似定理(Hornik, Stinchcombe, and White 1989; Funahashi 1989; Cybenko 1989)。普遍性扩展到标准RNN (Funahashi, 1989)，甚至连续时间RNN(Funahashi and Nakamura, 1993)。通过仔细考虑，我们还可以证明LTC也是通用近似器。

　　证明的主要思想是定义一个n维动态系统并将其放入一个高维系统。第二个系统是LTC。LTC的普遍性证明与CT-RNN的证明的根本区别(Funahashi and Nakamura, 1993)在于两种系统的语义上的区别，其中LTC网络在其时间常数模块中包含一个非线性输入相关项，这使得证明的部分不平凡。

　　通用近似定理广泛地探索了神经网络模型的表达能力。但是，该定理没有为我们提供关于不同神经网络结构之间的分离位置的基础度量。因此，需要更严格的表达量度来比较模型，尤其是比较那些专门用于时空数据处理的网络，例如LTC。据推测，在定义静态深度学习模型的表达量度方面取得的进展(Pascanu, Montufar, and Bengio 2013; Montufar et al. 2014; Eldan amd Shamir 2016; Poole et al. 2016; Raghu et al. 2017)可能可以帮助衡量时间连续模型在理论上和定量上的表现力，我们将在下一部分中进行探讨。

5.1 Measuring expressivity by trajectory length

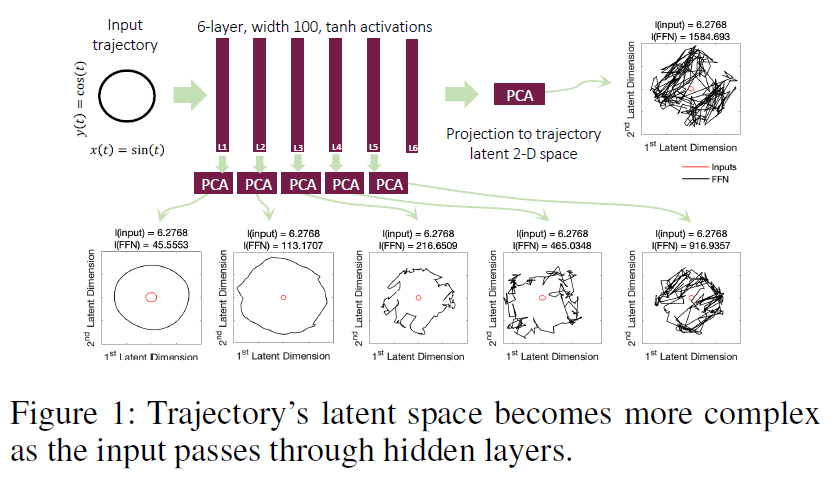
　　衡量表达能力时必须考虑到给定网络的容量(深度，宽度，类型和权重配置)，学习系统可以计算出多少复杂程度。静态深层网络的统一表达量度是(Raghu et al. 2017)。在这种情况下，人们会评估深度模型如何逐步将给定的输入轨迹(例如，圆形二维输入)转换为更复杂的模式。

　　然后我们可以对得到的网络激活进行主成分分析(PCA)。随后，我们在二维隐空间中测量输出轨迹的长度，以揭示其相对复杂性(见图1)。轨迹长度定义为给定轨迹I(t)的弧长(例如，二维空间中的圆)(Raghu et al. 2017)：。通过建立轨迹长度增长的下限，可以在浅层和深层结构的网络之间设置障碍，而不考虑对网络权重配置的任何假设(Raghu et al. 2017)，这与许多其他表现力度量不同(Pascanu, Montufar, and Bengio 2013; Montufar et al. 2014; Serra, Tjandraatmadja, and Ramalingam, 2017; Gabrié et al. 2018; Hanin and Rolnick, 2018、2019; Lee, Alvarez-Melis, and Jaakkola, 2019)。我们将静态网络的轨迹空间分析扩展到时间连续(TC)模型，并对轨迹长度下界以比较模型的表达能力。为此，我们设计了具有共享 f 的神经ODE、CT-RNN和LTC的实例。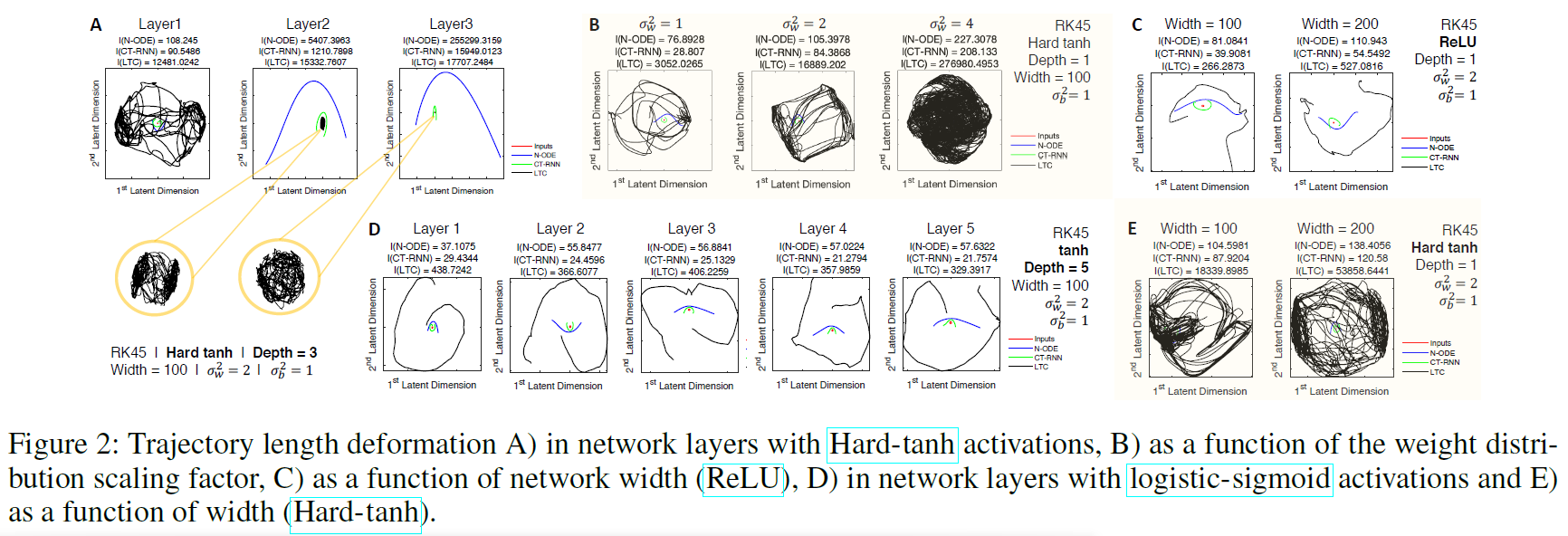这些网络由权重和偏差初始化。然后，我们通过使用不同类型的ODE解算器对任意权重分布执行前向传播模拟，同时将网络暴露于循环输入轨迹I(t) = {I₁(t) = sin(t), I₂(t) = cos(t)} (对于t ∈ [0, 2π])。通过观察隐含层激活的前两个主成分(平均方差超过80%)，我们观察到LTC的持续更复杂的轨迹。图2给出了我们的经验观察一瞥。所有的网络都由一个可变步长的Dormand-Prince显式Runge-Kutta(4,5)求解器(Dormand-Prince 1980)实现。我们有以下观察结果：I）在硬tanh和ReLU激活的情况下，神经ODE和CT-RNN的轨迹长度呈指数增长(图2A)，其潜伏期的形状不变，而与它们的权重分布无关。II）LTC在硬tanh和ReLU设计时，轨迹长度的增长速度较慢，并且妥协于实现很大的复杂度(图2A、2C和2E)。III）除了由硬tanh和ReLU激活建立的多层时间连续模型外，在所有情况下，我们都观察到LTC网络的更长和更复杂的潜在空间行为(图2B至2E)。IV）与静态深度网络(图1)不同，我们发现在由tanh和sigmoid实现的多层连续时间网络中，轨迹长度不随深度增长(图2D)。V）最后，我们观察到TC模型中的轨迹长度随模型的激活、权重和偏差分布、方差、宽度和深度而变化。我们在图3中更系统地展示了这一点。VI）轨迹长度随网络宽度线性增长(图3B——注意对数标度Yaxis中曲线的对数增长)。VII）随着方差的增加，增长速度快得多(图3C)。VIII）轨迹长度不愿意选择ODE解算器(图3A)。IX）激活函数使TC系统探索的复杂模式多样化，ReLU和硬tanh网络显示LTC的更高复杂性。一个关键的原因是每个层的细胞之间存在反复的链接。计算深度定义(L)。对于时间连续网络中的一个隐含层 f，L是解算器为每个输入样本所采取的平均集成步骤数。注意，对于n层的 f，我们将总深度定义为n x L。这些观测结果使我们为连续时间网络的轨迹长度的增长制定了下限。

　　该证明在附录中提供。对于具有分段线性激活的深层网络建立的轨迹长度范围，它遵循与(Raghu et al. 2017)类似的步骤，并由于连续时间设置而需要仔细考虑。构造证明，以便我们在主成分域中的d + 1层中的隐含状态梯度范数与右手范数的期望之间建立神经ODE和CT-RNN的微分方程的另一侧，然后回滚递归以到达输入。

　　注意，为了降低问题的复杂性，我们仅对隐含状态图像的正交分量，因此我们在定理的陈述中对输入I(t)进行了假设(Raghu et al. 2017)。接下来，我们找到LTC网络的下限。

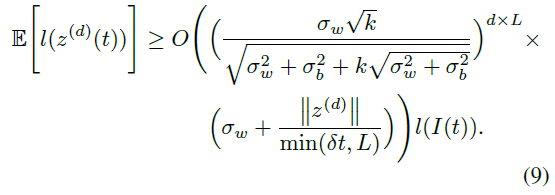
　　该证明在附录中提供。一个粗略的轮廓：我们分别构造隐含状态梯度的范数和LTC右侧分量之间的递归，这些递归逐步建立边界。

5.2 Discussion of the theoretical bounds

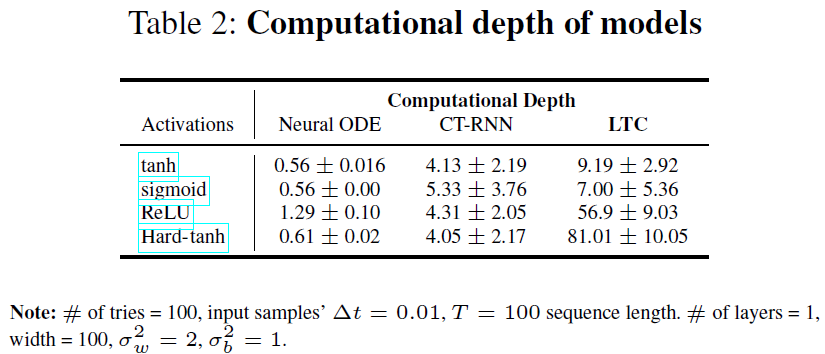
　　I）正如预期的那样，神经ODE的边界与n层静态深层网络的边界非常相似，但与求解器步数L的指数相关性除外。II）根据指数的基，与神经ODE相比，CT-RNN的边界表明其轨迹长度更短。该结果始终与我们在图2和3中显示的实验相匹配。III）图2B和图3C显示了LTC轨迹长度的增长快于线性，这是权重分布方差的函数。LTC在公式9中显示的下限确认了这一点。IV）LTC的下限还描绘了轨迹长度随宽度k的线性增长，这验证了3B中提出的结果。V）给定表2中模型L对硬tanh激活的计算深度，在第5节的实验中，神经ODE，CT-RNN和LTC的计算下限证明了LTC网络的轨迹长度更长。在一组现实生活中的时间序列预测任务中评估LTC的表达能力。

6 Experimental Evaluation

6.1 Time series predictions. 在一系列不同的现实生活中受监督的学习任务中，我们针对最先进的离散RNN，LSTM (Hochreiter and Schmidhuber 1997)，CT-RNN (ODE-RNN) (Funahashi and Nakamura 1993; Rubanova, Chen, and Duvenaud 2019)，连续时间门控循环单元(CT-GRU)(Mozer, Kazakov, and Lindsey 2017)，以及由四阶Runge-Kutta求解器构造的神经ODE，如(Chen et al. 2018)所述评估了所提出的ODE求解器实现的LTC的性能。结果总结在表3中。实验装置在附录中提供。在七个实验中有四个实验中，与其他RNN模型相比，我们观察到LTC的性能提高了5％至70％，而在其他三个实验中，性能却相当(参见表3)。

6.2 Person activity dataset. 我们在两个不同的框架中使用(Rubanova, Chen, and Duvenaud 2019)中描述的"人类活动"数据集。数据集由6554个人类活动序列(例如躺着，走路，坐着)组成，周期为211毫秒。我们设计了两个实验框架来评估模型的性能。在第一设置中，基准是之前描述的模型，输入表示形式保持不变(详细信息在附录中)。LTC的性能优于所有模型，尤其是CTRNN和神经ODE，如表4所示。请注意，CT-RNN结构等效于(Rubanova, Chen, and Duvenaud 2019)中描述的ODE-RNN，其区别在于具有状态阻尼因子τ。

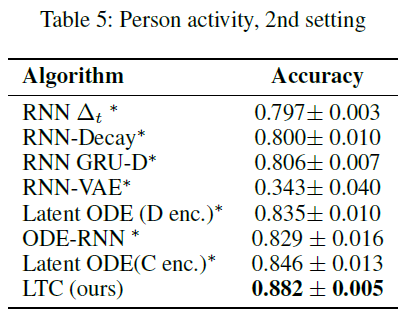
　　在第二设置中，我们精心设置了实验以匹配(Rubanova, Chen, and Duvenaud 2019)所做的修改(请参见补充材料)，以在LTC和(Rubanova, Chen, and Duvenaud 2019)中讨论的更多样化的RNN变体集之间进行公平的比较。与其他型号相比，LTC具有出众的性能和较高的利润率。结果总结在表5中。

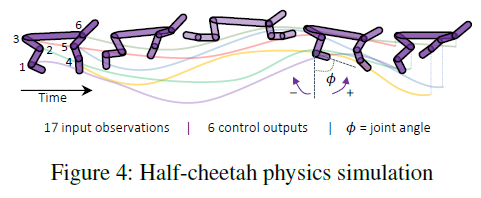
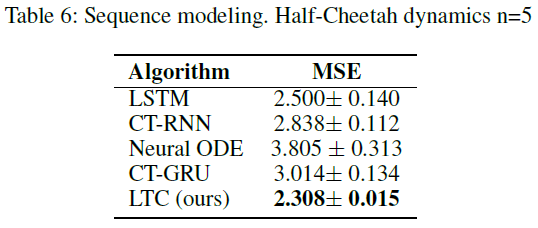
6.3 Half-Cheetah kinematic modeling. 我们打算评估连续时间模型捕获物理动态的能力。为此，我们收集了由MuJoCo物理引擎(Todorov, Erez, and Tassa 2012)生成的针对HalfCheetah-v2 gym环境的预训练控制器的25个部署(Brockman et al. 2016)。然后的任务是以自回归方式拟合观察空间的时间序列(图4)。为了增加难度，我们用随机动作覆盖了5％的动作。测试结果列在表6中，其根源在于LTC与其他模型相比的优越性。

7 Related Works

Time-continuous models. TC网络已变得空前流行。这是由于多项优势的体现，例如自适应计算，更好的连续时间序列建模，内存和参数效率(Chen et al. 2018)。许多替代方法试图改善和稳定伴随方法(Gholami, Keutzer, and Biros 2019)，在特定情况下使用神经ODE (Rubanova, Chen, and Duvenaud 2019; Lechner et al. 2019)并对它们进行表征更好(Dupont, Doucet, and Teh 2019; Durkan et al. 2019; Jia and Benson 2019; Hanshu et al. 2020; Holl, Koltun, and Thuerey 2020; Quaglino et al. 2020)。在这项工作中，我们研究了神经ODE的表达能力，并提出了一个新的ODE模型以提高其表达能力和性能。

Measures of expressivity. 大量当前工作试图找到问题的答案，例如为什么更深层的网络和特定的结构表现良好，以及浅层网络和深层网络的近似能力之间的界限在哪里？在这种情况下(Montufar et al. 2014)和(Pascanu, Montufar, and Bengio 2013)建议对神经网络的线性区域数量进行计数以衡量表达力(Eldan and Shamir 2016)表明存在一个较小的网络无法产生的径向函数类，(Poole et al. 2016)研究了瞬态混沌对神经网络的指数表达能力。

　　这些方法引人注目；但是，它们受限于给定网络的特定权重配置，以降低与(Serra, Tjandraatmadja, and Ramalingam 2017; Gabrié et al. 2018; Hanin and Rolnick 2018, 2019; Lee, Alvarez-Melis, and Jaakkola 2019)。(Raghu et al. 2017)引入了一个相互关联的概念，即通过轨迹长度量化给定静态网络的表达能力，我们将其表达能力分析扩展到时间连续网络，并为轨迹长度的增长提供了下界，并称其具有出色的逼近能力的LTC。

8 Conclusions, Scope and Limitations

　　我们研究了通过线性ODE神经元和特殊的非线性权重组合获得的新型时间连续神经网络模型。我们证明了它们可以通过任意变量和固定步长的ODE求解器有效地实现，并且可以通过时序反向传播进行训练。与标准和现代深度学习模型相比，我们在有监督的学习时间序列预测任务中展示了其有限而稳定的动态性，卓越的表现力和替代性能。

Long-term dependencies. 与时间连续模型的许多变体相似，当通过梯度下降训练时，LTC会表现出梯度消失现象(Pascanu, Mikolov, and Bengio 2013; Lechner and Hasani 2020)。尽管该模型显示了在各种时间序列预测任务上的希望，但对于以当前格式学习长期依存关系，它们并不是显而易见的选择。

Choice of ODE solver. 时间连续模型的性能在很大程度上依赖于其数值实现方法(Hasani 2020)。虽然LTC在使用先进的可变步长求解器和此处介绍的Fused固定步长求解器时表现良好，但是当使用现成的显式Euler方法时，其性能会受到很大影响。

Time and Memory. 与更复杂的模型(例如LTC)相比，神经ODE的速度非常快。但是，它们缺乏表现力。我们以当前格式提出的模型大大提高了TC模型的表达能力，但代价是时间和内存复杂性的增加，这些都必须在将来进行研究。

Causality. 用时间连续微分方程语义描述的模型固有地具有因果结构(Schölkopf 2019)，特别是配备有循环机制以将过去的经验映射到下一步预测的模型。研究高性能循环模型(如LTC)的因果关系将是一个令人兴奋的未来研究方向，因为它们的语义类似于具有双线性动态系统近似(Penny，Ghahramani, and Friston 2005)的动态因果模型(Friston, Harrison, and Penny 2003)。因此，自然的应用领域将是连续时间观察和动作空间中的机器人控制，在这些空间中，因果结构(如LTC)可以帮助改善推理(Lechner et al. 2020a)。

Supplementary Materials

S1 Proof of Theorem 1

S2 Proof of Theorem 2

S3 Proof of Theorem 3

S3.1 Proof of the Theorem:

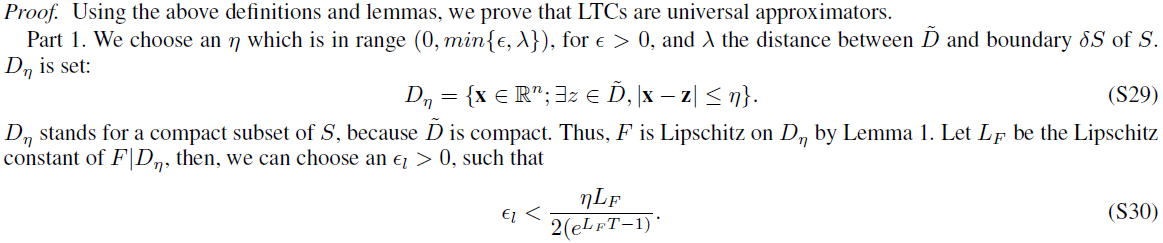
S4 Proof of Theorem 4

　　在本节中，我们将描述我们的数学概念，并重新讨论陈述证明所需的概念。我们关于时间连续神经网络表达能力的理论结果的主要陈述主要建立在(Raghu et al.2017)中介绍的静态深层神经网络的表达能力测度(轨迹长度)上。因此，由于模型的连续性，遵循类似步骤并仔细考虑是很直观的。

S4.1 Notations

S4.2 Beginning of the proof of Theorem 4

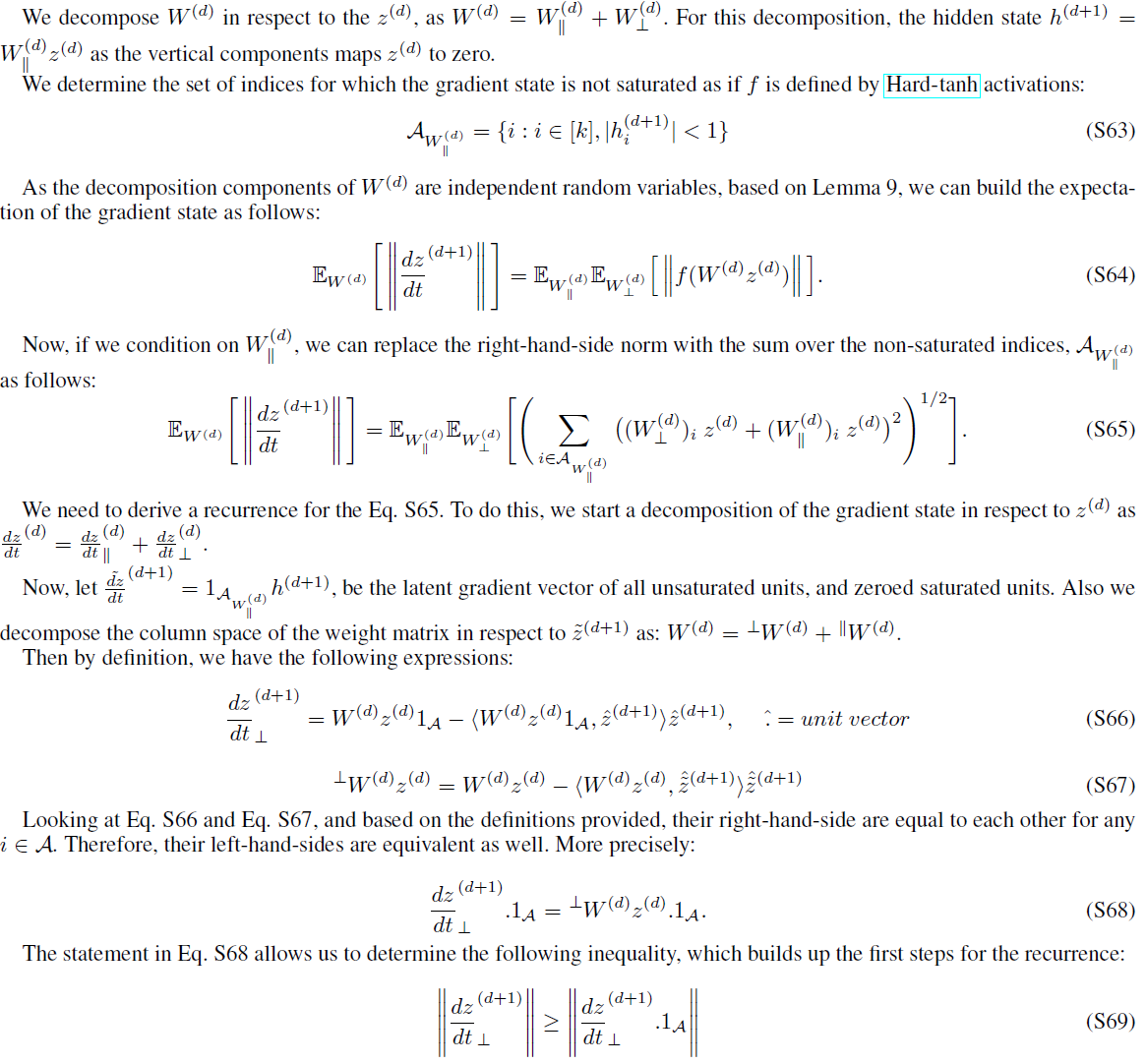
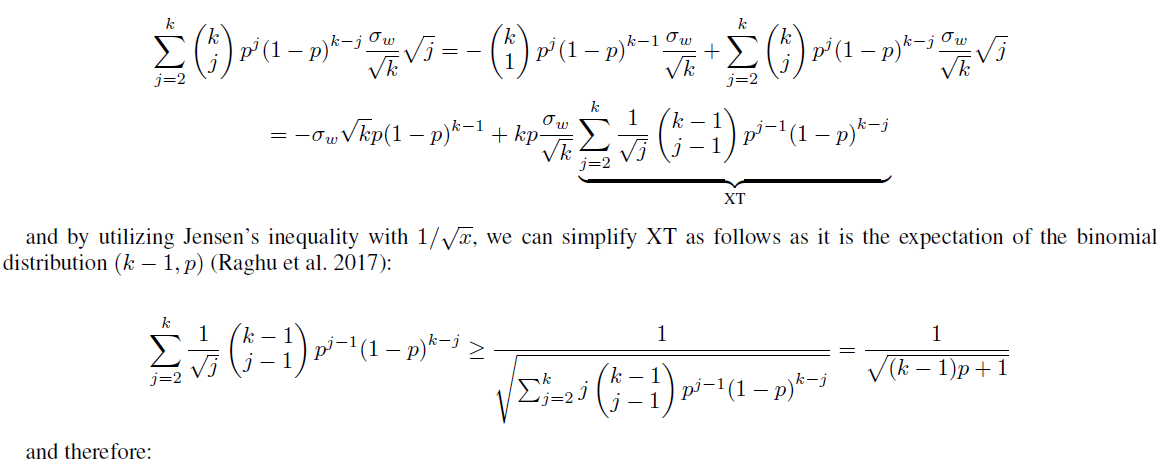
Proof of Theorem 5

Distribution of parameters of LTCs

S5 Experimental Setup - Section 6

S6 Hyperparameters and Parameter counts - Tables 3, 4, and 6

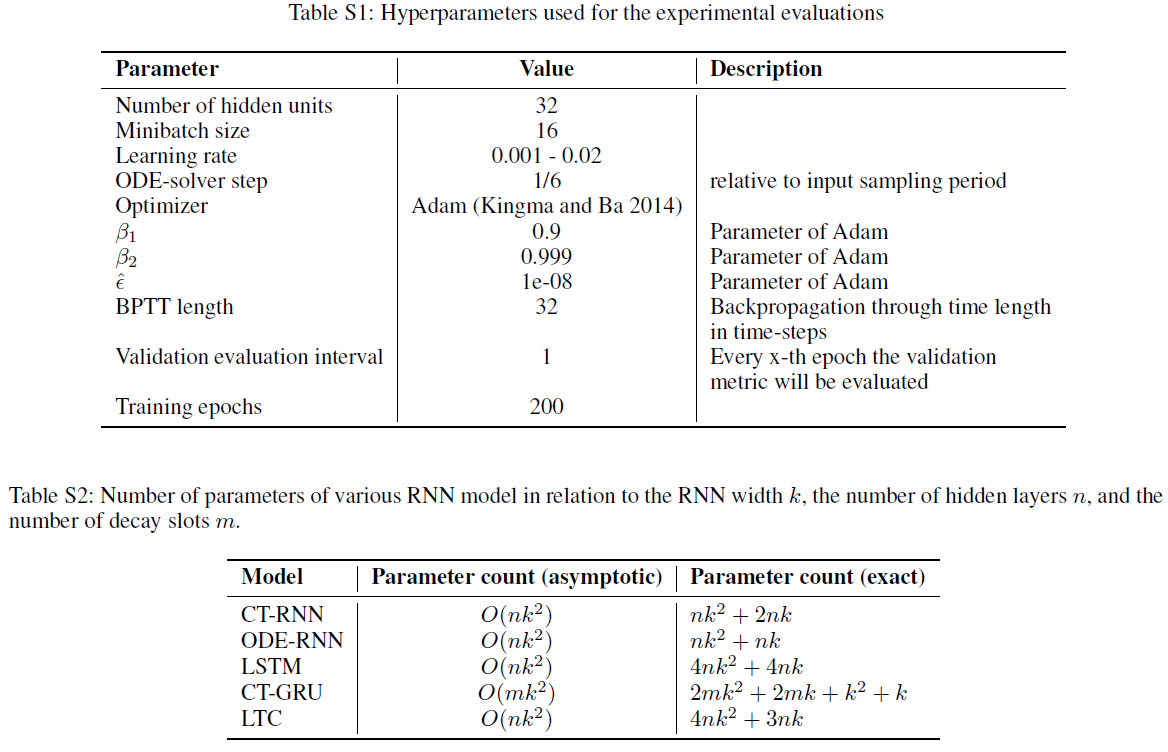
S7 Additional trajectory space representations: 

　　提供的结果的轨迹空间表征可以在此获取: https://www.dropbox.com/s/ly6my34mbvsfi6k/additional_LTC_neurIPS_2020.zip?dl=0

S8 Trajectory Length results

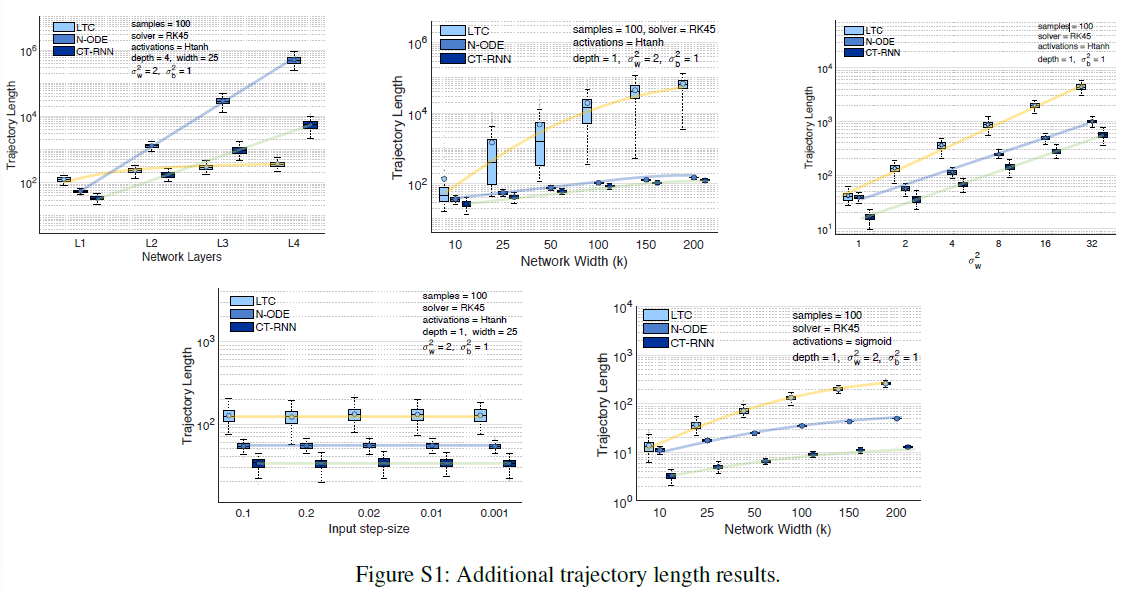
S9 Code and Data availability

　　有代码和数据均可在以下位置公开访问：https://github.com/raminmh/liquid_time_constant_networks.