前面两篇博客介绍了线性表的顺序存储与链式存储以及对应的操作,并且还聊了栈与队列的相关内容。本篇博客我们就继续聊数据结构的相关东西,并且所涉及的相关Demo依然使用面向对象语言Swift来表示。本篇博客我们就来介绍树结构的一种:二叉树。在之前的博客中我们简单的聊了一点树的东西,树结构的特点是除头节点以外的节点只有一个前驱,但是可以有一个或者多个后继。而二叉树的特点是除头结点外的其他节点只有一个前驱,节点的后继不能超过2个。
本篇博客,我们只对二叉树进行讨论。在本篇博客中,我们对二叉树进行创建,然后进行各种遍历,最后将二叉树进行线索化。在Demo实现之前,我们先对二叉树的概念及其特性进行介绍,然后在给出具体的代码实现。
一、二叉树的特性
上面我们已经提到过,一个除头结点外,每个节点只有一个前驱,有零到两个后继的树即为二叉树。在二叉树中,一个节点可以有左节点或者左子树,也可以有右节点或者右子树。一些特殊的二叉树,比如斜二叉树、满二叉树、完全二叉树等等就不做过多赘述了。说这么多,不如看一张图来的直观。下方就是一个典型的二叉树。

了解二叉树,理解其特性还是比较重要的。基于二叉树本身的逻辑结构,下方是二叉树这种数据结构所具备的特性。
- 特性1:在二叉树的第i层上至多有2^(i-1)(i >= 1)个节点。
- 这一特性比较好理解,如果层数是从零开始数的话,那么低i层上的节点数就是2^i,因为二叉树层与层之间的节点数是以2的指数幂进行增长的。如果根节点算是第0层的话,那么第n层的节点数就是2^n次幂。
- 特性2:深度为k的二叉树至多有2^k-1(k>=1)个节点。
- 这一特性也是比较好理解的, 由数学上的递加公式就可以很容易的推出来。由特性1易知每层最多有多少个节点,那么深度为k的话,说明一共有k层,那么共有节点数为:2^0 + 2^1 + 2^2 + 2^(k-1) = 2^k - 1。
- 特性3:二叉树的叶子节点数为n0, 度为2的节点数为n2, 那么n0 = n2 + 1。
- 这一特性也不难理解,推出n0 = n2 + 1这个公式并不难。我们假设叶子节点,也就是度数为0的节点的个数为n0, 度数为1的节点为n1, 度数为2的节点n2。那么二叉树的节点总数 n = n0 + n1 + n2。因为除了根节点外其余的节点入度都为1,所以二叉树的度数为n-1,当然度的个数可以使用出度来算,即为2*n2+n1,所以n-1=2*n2+n1。以n=n0+n1+n2与n-1=2*n2+n1这两个公式我们很容易的推出n0 = n2 + 1。
- 特性4:具有n个结点的完全二叉树的深度为log2n + 1 (向下取整,比如3.5,就取3)。
- 这个特性也是比较好理解的,基于完全二叉树的特点,我们假设完全二叉树的深度为k, 那么二叉树的结点个数的范围为2(k-1)-1 <= n <= 2k-1。由这个表达式我们很容易推出特性4。
二、二叉树的创建
上面介绍完二叉树的特性后,接下来我们要做的就是将二叉树进行存储。当然一般存储二叉树的结构是以二叉链表的形式来存储的。二叉链表的结构类似于双向链表,二叉链表的节点也是有两个结点指针的,一个指向左子树,一个指向右子树。接下来我们要使用二叉链表的形式来存储我们的二叉树。
1.先序创建二叉树
在创建二叉树之前,我们先了解一个什么是先序遍历。先序遍历就是先遍历根结点,然后遍历左子树,最后遍历右子树。我们就以此规则来创建二叉树,换句话说,我们有一个数据序列,将依照这个序列按照先序创建二叉树的原则来创建该二叉树,先创建二叉树的根节点,然后再创建二叉树的左子树,然后再创建右子树。而这个创建的二叉树的先序遍历的结果就是我们之前输入的数据序列。下方就是先序创建二叉树的原理图。
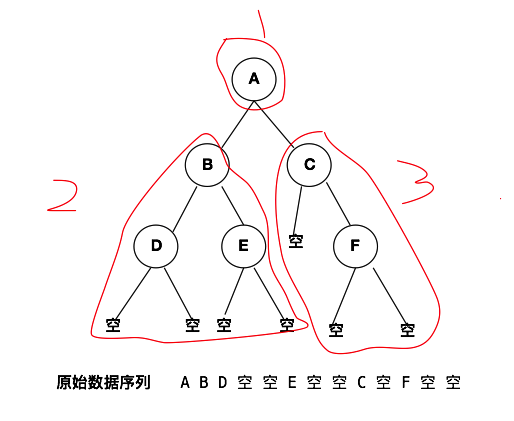
从上面的分析我们不难看出,我们要先创建根节点,然后创建左子树,最后创建右子树。因为左子树和右子树都是二叉树,所以创建左子树和右子树是原问题的子问题。也就是说子问题与原问题解决方案一致,这种情况下就可以使用递归的思想来解决。我们先将上述二叉树的结构转换成二叉链表的形式直观的感受一下,然后再将其使用代码的形式进行表示即可。下方这个截图就是上述二叉树的二叉链表的存储结构。每个节点都有左指针与右指针,分别自己的左子节点和右子节点。如果没有子节点就为空。

2.先序创建二叉树的代码实现
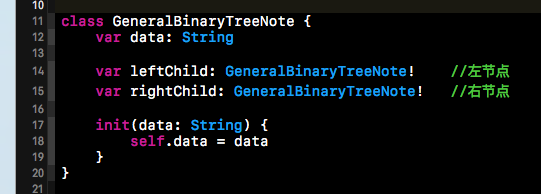
上面我们分析了二叉链表的结构,接下来我们就来创建二叉链表了。首先我们得创建二叉链表的节点类,之前我们用C语言来实现二叉树的时候,是使用的结构体来实现的二叉链表的节点,因为C语言是面向过程的语言,根本就没有类这个概念。因为此刻我们是使用的面向对象语言,所以我就可以使用一个类来表示我们二叉链表的节点了。下方这个GeneralBinaryTreeNote就是二叉链表的类。data属性存储的就是树节点中所存储的值,而leftChild就指向左节点的内存地址,而rightChild就指向右节点的内存地址。
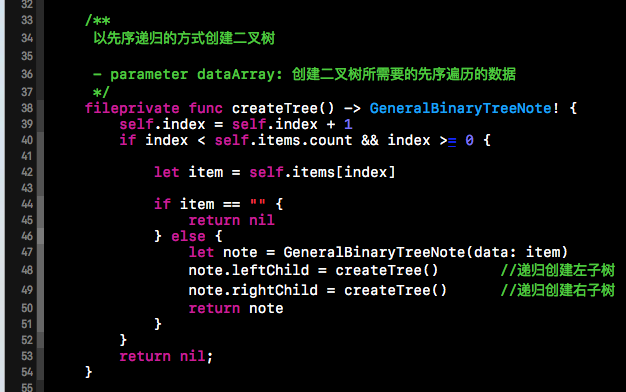
上面我们已经说过,先序创建二叉树的过程是可以用递归来表示的,所以我们就递归的去创建我们想要创建的二叉树。下方就是先序创建二叉树的核心代码,self.items中存储的是二叉树的节点信息。经过下方函数的递归执行,就可以创建出我们想要的二叉树了。从下方的递归过程我们就明显的能看出是先序创建的二叉树。先创建的根节点,然后递归创建左子树,然后在递归创建右子树。
下方就是我们二叉树的初始化过程,下方在初始化过程中主要是调用上方的这个方法,将items数组中存储的值转换成二叉链表的存储结构。items数组中的空字符串,表明该节点为空。
![]()
其实上面实例中所创建的二叉树的结构就是下方的结构。

三、二叉树的遍历
聊二叉树怎么能没有二叉树的遍历呢,下方就会给出几种常见的二叉树的遍历方法。在遍历二叉树的方法中一般有先序遍历,中序遍历,后续遍历,层次遍历。本篇博客主要给出前三种遍历方式,而层次遍历会在图的部分进行介绍。二叉树的层次遍历其实与图的广度搜索是一样的,所以这部分放到图的相关博客中介绍。下方会给出几种遍历的具体方式,然后给出具体的代码实现。
二叉树的先、中、后遍历,这个先中后指的是遍历根节点的先后顺序。先序遍历:根左右,中序遍历:左根右,后序遍历:左右根。下方将详细介绍到。
1.先序遍历
关于先序遍历,上面已经介绍过一些了,接下来再进行细化一下。先序遍历,就是先遍历根节点然后再遍历左子树,最后遍历右子树。下图就是我们上面创建的二叉树的先序遍历的顺序,由下方的示例图就可以看出先序遍历的规则。一句话总结下方的结构图:根节点->左节点->右节点。下方先序遍历的顺序为:A B D 空 空 E 空 空 C 空 F 空 空 。

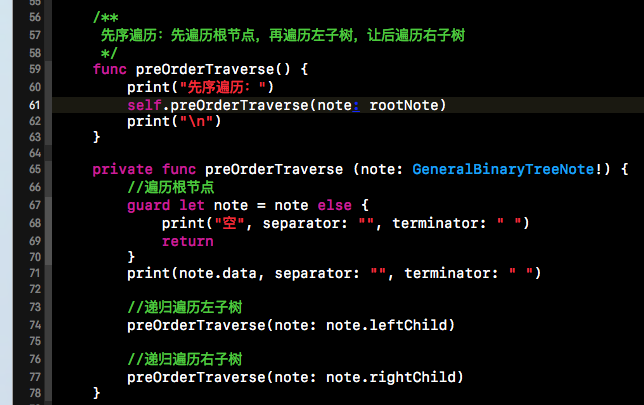
上面给出了原理,接下来又到了代码实现的时候了。在树的遍历时,我们依然是采用递归的方式,因为无论是左子树还是右子树,都是二叉树的范畴。所以在进行二叉树遍历时,可以使用递归遍历的形式。而先序遍历莫非就是先遍历根节点,然后递归遍历左子树,最后遍历右子树。下方就是先序遍历的代码实现。在下方代码中,如果左节点或者右节点为空,那么我们就输出“空”。
2.中序遍历
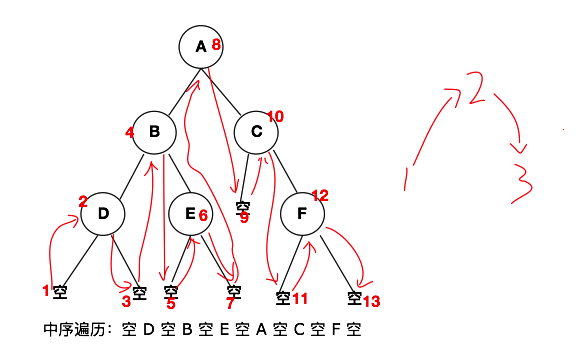
中序遍历,与先序遍历的不同之处在于,中序遍历是先遍历左子树,然后遍历根节点,最后遍历右子树。一句话总结:左子树->根节点->右子树。下方就是我们之前创建的树的中序遍历的结构图以及中序遍历的结果。
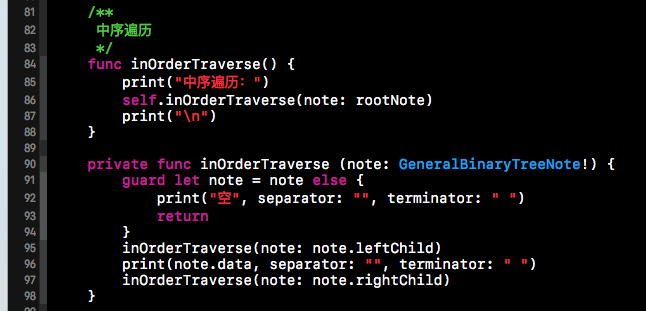
中序遍历的代码实现与先序遍历的代码实现类似,都是使用递归的方式来实现的,只不过是先递归遍历左子树,然后遍历根节点,最后遍历右子树。下方就是中序遍历的代码具体实现。
3.后序遍历
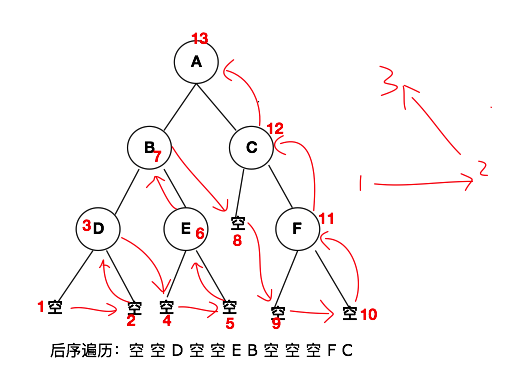
接下来聊一下二叉树的后序遍历。如果上面这两种遍历方式理解的话,那么后序遍历也是比较好理解的。后序遍历是先遍历左子树,然后再遍历右子树,最后遍历根节点。与上方的表示方法一直,首先我们给出表示图,如下所示:
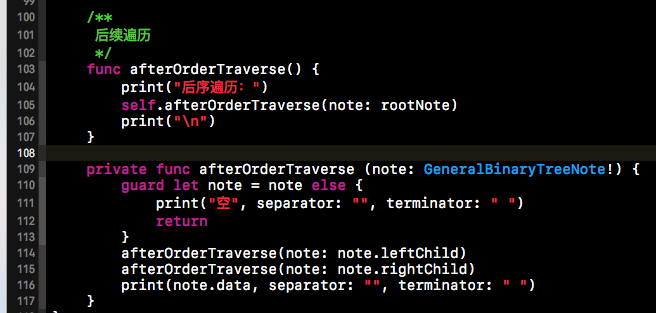
后序遍历的代码就不做过多赘述了,与之前两种依然类似,只是换了一下遍历的顺序。下方就是二叉树后序遍历的代码实现。
4、层次遍历
二叉树的层次遍历就不是二叉树这种数据结构所独有的了。后面的博客中我们会介绍到图这种数据结构,在图中有一个广度搜索,放到二叉树中就是层次遍历。也就是说二叉树的层次遍历,就是图中以二叉树的根节点为起始节点的广度搜索(BFS)。本篇博客就不给出具体的代码了,后面的博客会给出BFS的具体算法。当然在之前的博客中有图的BFS以及DFS。不过是C语言的实现。下方就是二叉树层次遍历的实例图。
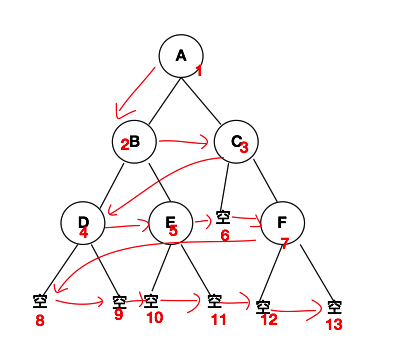
四、二叉树的线索化
二叉树的线索化,起始就是利用二叉树中的空的节点来将二叉树转换成链表的结构。当然只针对中序遍历的序列。从上面中序遍历的结果中,我们不难看出,有节点的值与空指针是间隔的(空 D 空 B 空 E 空 A 空 C 空 F 空)。也就是说好多空的左指针与右指针浪费了。二叉树的线索化,就是在中序遍历中,将空的左子树的指针指向其中序遍历结果的前驱,而空的右子树指针指向中序遍历中该节点的后继。具体的示意图如下所示:
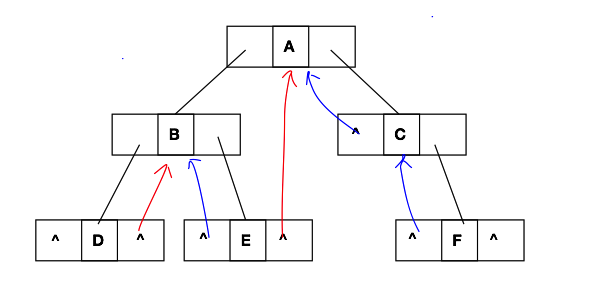
从上面的图中我们不难看出。在被线索化的二叉树中,左节点指针不止指向左节点,而且有可能指向节点的前驱。而右节点指针不仅仅是指向右节点的指针,还有可能指向该节点在中序遍历中的后继节点。为了标记指针是指向子节点还是指向前驱或者后继,所以我们要添加相应的标志位来标记指针指向的是那些节点。下方就是我们改造后的二叉树的节点:
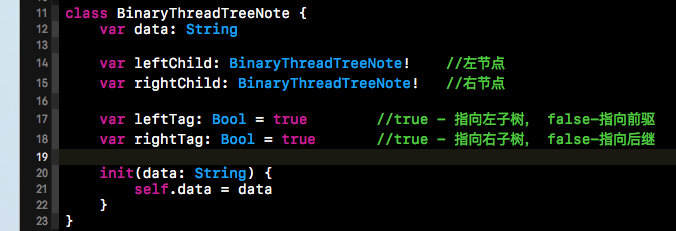
改造完节点后,我们就可以将二叉树进行线索化了,下方就是被线索话的二叉树的代码。可以看出,下方的代码的整体步骤与二叉树的中序遍历类似。
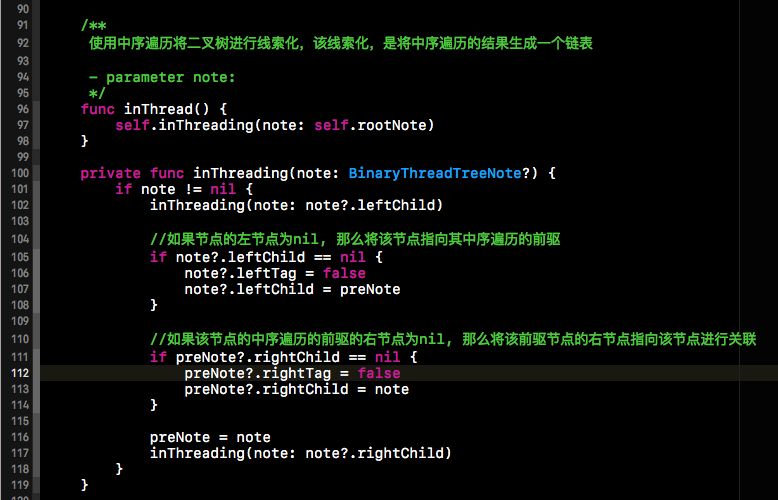
被线索化的二叉树就可以根据我们添加的线索进行中序遍历了,效率要比递归的中序遍历要高的多,如下所示:
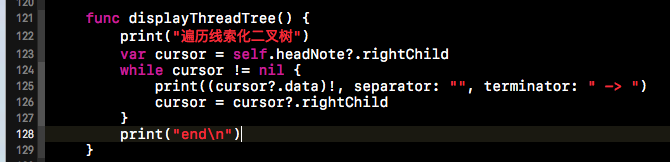
五、测试用例
上面的代码都是如何去实现了,接下来到了我们测试的时间了,下方这段代码段是我们的测试用例。首先给出二叉树的节点信息,然后先序的创建一棵二叉树。然后给出二叉树的先、中、后续遍历,最后给出二叉树线索话的结果。
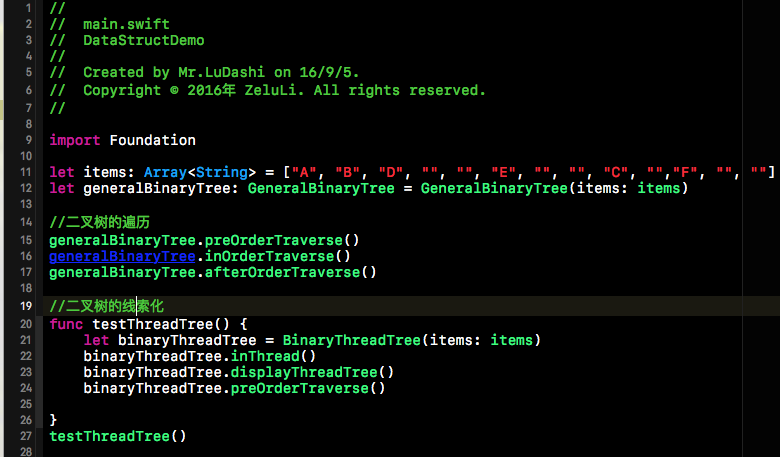
下方截图就是我们测试用例的运行结果,一目了然,在此就不做过多的赘述了。
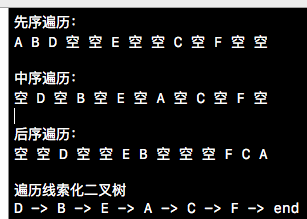
本篇博客的篇幅也够长的了,就先到这儿吧,上述实例的完整Demo会在github上进行分享, 下篇博客我们将要介绍图的邻接链表和邻接矩阵,以及图的BFS和DFS。
github链接地址:https://github.com/lizelu/DataStruct-Swift/tree/master/BinaryTree