关键词:反射率 反射因子 BRDF
作者:李二
日期:13/11/2020 - 15/11/2020
0. 前言
上篇博文末尾提到,采用
反射度量 reflectance quantities而非辐射度量 radiant quantities来描述地物的本质属性是比较合适的,因为这样就避免了因入射辐照度的差异带来的问题。
关于
反射度量这部分,很多概念非常容易让人疑惑不解,我觉得这主要是由两方面原因造成的:
不同书籍文献资料写的确有出入,同一个概念(如反射率)有多种定义和公式表示方式。
直接将各种度量的定义塞给学生,而非从源头开始讲起为什么要这么定义和表示。
不同文献和书中的对反射率的称谓有所不同 因此我试图通过这篇博文去讲清楚,但是我依然不能保证自己的理解绝对正确,请读者辨别看待。
1. 从能量守恒出发
我们引出
反射、吸收、透射的概念,应当都是在能量守恒这一框架下的。能量守恒是我们所有工作的基本前提,然后我们想具体研究一下辐射在介质中的传输过程中,到底发生了什么:当入射光投射到某介质层时,人们注意到:
一部分辐射返回来了,因此叫做 反射;一部分辐射在穿过介质的时候被吸收了,因此叫做 吸收;一部分辐射穿透介质后出射了,因此叫做 透射。一共就这三部分,没其他的了。
我们假定
入射辐射通量 Φi (单位:W),反射辐射通量,吸收辐射通量,透射辐射通量,根据能量守恒定律:
那么有:
因此,我们记做:
, ,
,,分别叫做反射率、吸收率、透过率。
可以看到,这就是我们对于反射率最根本最朴素认知公式,那如果根据公式,反射率必然不能大于1,毕竟必然小于等于。
然而,我们在某些遥感产品中确实会发现
反射率大于1的现象,这其实是因为通常辐射通量无法直接测量得到,我们需要对上述公式进行转换,而转换后确实会发生反射率大于1的现象,我们后面慢慢讲。另外,注意到没有,我们用的是 而非 ,表明这里并没有方向性的考虑。
2. 地物反射率的定义与测量
请大家务必注意,下面的一些概念称谓使用的准确性和方向符号的使用,否则极易造成误解。
我们有时在一些文献中看到,反射率 是用
辐射通量密度进行定义的,即:
这当然没有任何问题。但是有些眼尖的看官会发现,咦,
反照率 Albedo的公式不就是这嘛。是的,如果你期望的是对介质或地表的
总体反射情况(我自创的,可能不精准,但不妨意会一下)进行描述,那么反射率其实就是反照率,根据上面这个公式,取值范围自然是0-1。这在地表辐射收支平衡的研究中使用的比较多,因为人们只关心地表的总反射,而不在意每个反射方向到底发生了什么。
另外,值得一说的是,辐射出射度是没办法直接测量的,因为它是半球反射的积分,所以通常需要BRDF模型才能算出来。
2.1. 朗伯表面的反射率
我们还是从最简单的开始讲起,朗伯表面的反射情况,如果要计算朗伯表面反射率,那么有:
我们发现朗伯表面的反射率最终可以表示为反射辐亮度与辐照度的函数,这样有什么好处呢?
好处就是,我们可以通过仅仅测量一个方向的辐亮度,就能把反射率计算出来。而且,朗伯表面各个方向的反射辐亮度相等。
特别要注意的是,这里的并非是 ,也就是说它并不具有方向性的特征。
2.2. 非朗伯表面的反射率
非朗伯表面就有点意思了,如果我们依然沿用上面公式中的:
就会发现,到这里就没办法继续进行下去了,因为非朗伯表面各个方向的辐亮度并不相等。那问题来了,对于非朗伯表面,怎么计算其反射率呢?
那只能把各个方向的获取到然后积分了。当然这并不现实,现实的做法是通过有限几个方向的辐亮度观测来拟合BRDF模型,然后得到各方向。
3. 地物二向性反射的表征与测量
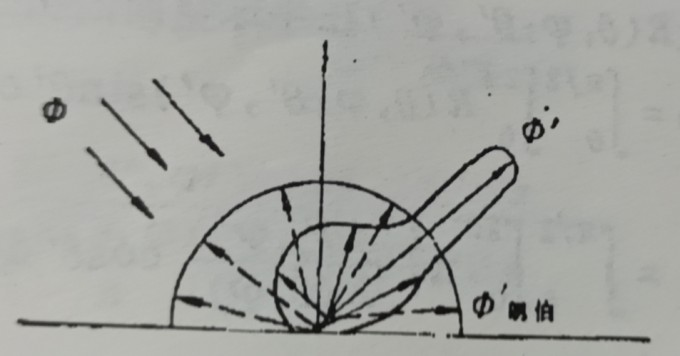
上篇博文中讲到,地表在接收到入射辐射后,会向整个空间的各个方向进行反射。
而人们有时会关心某些反射方向的反射情况,或者不同反射方向的反射有什么差异。 另外,又因为通常传感器测量地表反射辐射时仅能在一个方向(微立体角元)进行观测(不考虑多角度观测)。 因此,我们需要重点关注一下
如何描述地物在不同方向的反射情况。
3.1. 伟大的BRDF
人们发现,地物表面反射不仅仅具有方向性(
漫反射),而且各个方向的反射情况还和光入射的方式、入射角的大小有关,他们的变化都会引起反射辐射通量以及它在空间分布的变化。那自然地,我们想到不妨直接用方向的反射辐射通量比上方向的入射辐射,这多简单的事情:
其中为投影立体角,我们以后会讲(其实在系列博文1中就有,只是没有单独说)
然而,我们立刻就发现一个重要问题,按照这个公式,我们在测这个方向反射比值的同时,还必须知道观测时的立体角,这是相当不方便的,所以我们并不适用上述公式。
顺便说一句,上面这个往往被叫做
方向反射率。所以大家对于各种概念不要乱叫。
为了解决这一问题,能够更方便地描述地物的二向性反射特点:
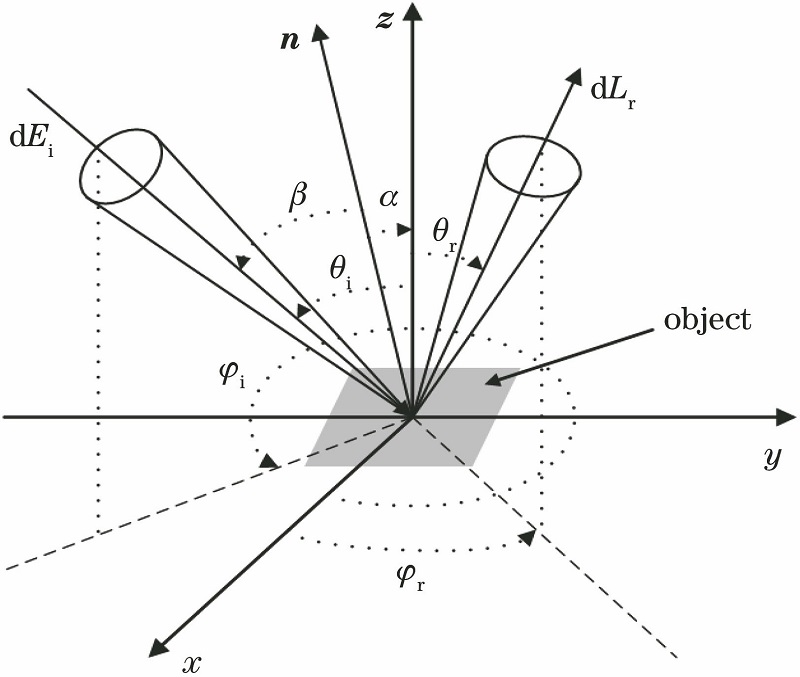
Fred E. Nicodemus于1965年提出采用二向反射分布函数 bidirectional reflectance distribution function(尽管首次提出时并非这么叫的)来描述不同入射角条件下物体表面在任意观测角的反射特性:
看到这,大家很容易有两个疑问:
为什么采用微分的形式即,而不直接用? 直观上看,为什么用除以,而不是除以? 其实Nicodemus在他文章中已经解释了这两个问题:
问题1答案:考虑到其他入射辐射(来自于其他光源的其他方向)也可能被散射到与相同的方向,那么净反射辐亮度 net reflected radiance其实是所有对贡献的反射辐射量的加和,而我们希望去精确地描述单一入射方向与单一反射方向的情况,因此采用,即来自方向地表辐照度的微增量与其所引起的方向反射辐亮度的微增量之间的比值。(不过有时我们不那么严格,不加这个微分符号也没关系)
问题2答案:Nicodemus也是从 方向反射率出发的:
为了避免受到反射投影立体角大小的影响,可以等式两边同时除以它。同时分母中的也不好独立描述,且不容易测量,又,所以有(因此
BRDF的单位是):
其实,说到底用用除以就是为了
测量的方便。这样我们就能很完美地描述地物的二向性反射情况了。
关于入射辐亮度不容易测量这个事,有必要稍微展开说一下:
首先说
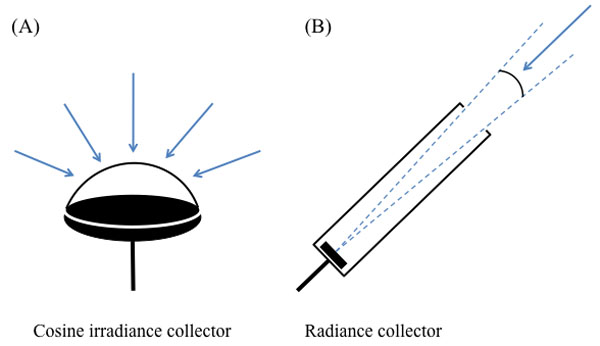
辐亮度 radiance测量的方法:其实就是用辐射度测量仪 radiance collector进行测量(图3-1 B)。辐射度测量仪有一个长筒控制光线只能从一个很小的立体角进入测量仪,根据公式就能够得到辐亮度了。很容易发现,反射辐亮度是很容易测量的,就是按照上面的方法。然而,入射辐亮度却难以测量,这是因为:
必须保证光源正好覆盖辐射度测量仪的开口立体角:
如果开口立体角大了,则微分面元实际接收的辐射通量会比测量值大,导致测量值比实际值小; 如果开口立体角小了,则微分面元实际接收的辐射通量会比测量值小,导致测量值比实际值大。 而辐照度测量就不受到立体角的束缚:
只要保证光源很小,而且没有来自其他方向的光干扰,通过辐照度测量仪(图3-1 A)就能准确测量出入射方向的辐照度。
小注:定义辐照度的时候并不涉及方向性的问题,但是如果单纯的只有直射光,那么辐照度的能量来源只有这一个方向,因此也就有了这一表达。
特殊地,对于理想朗伯表面(完全反射)的BRDF,我们有:
顺便说一下,BRDF已经是遥感物理与计算机图形学中渲染的重要基础。
3.2. 定义的严格性VS测量的实用性
我们不得不承认,BRDF定义是非常严格和明确地,可以从理论上完美地表征地物的非朗伯特性。然而,令人遗憾的是,它的测量条件极为苛刻,往往难以实现:
入射方向辐照度的测量十分困难,因为难以保证没有来自其他方向光的干扰。 反射方向的辐亮度可能会受到其他光源向该方向的反射辐射的干扰。 但并没有说BRDF绝对不能够测量,总是有办法的,但是这在野外条件下基本是行不通的。于是,我们想,有没有对测量更友好的二向性反射特征表征方式呢,让我们不必测量入射辐照度了?
人们想到用一个理想朗伯反射表面作为参考基准,然后计算地物表面反射与朗伯表面反射的差异,这样就避免了上述的两个难题。于是诞生了
二向反射因子 bidirectional reflectance factor (BRF):定义:在相同的方向入射辐射和观测条件下,相同微分面元下,地物表面的反射辐射通量与理想朗伯表面的反射辐射通量之比。
这里要注意了,由上面这个公式我们可以做出如下三种形式的继续推导:
(1) :
(2) :
因为对于理想朗伯表面(即完全反射,没有吸收,反射率为1),所以有。当然如果是反射率小于1的朗伯表面,则有。
(3) :
这三个推导公式都有各自的价值,我们逐个说一下:
(1)式告诉我们在地面-航空平台上如何进行的测量:通常实验人员在地表放置
朗伯反射标准板,所以容易测量出,然后就能算BRF了。此时,我们习惯称测量的值为
二向性反射因子而非二向性反射率。(2)式告诉我们通常卫星平台是怎么得到BRF的:通过大气辐射传输模型,可以计算出入射辐照度,传感器经辐射校正后又能够得到,自然BRF就可以计算了。
此时,我们习惯称测量的值为
二向性反射因子,或者有的书中和产品中也称为二向性反射率。(3)式告诉我们,有了BRF之后如何计算BRDF,这样就不用测量BRDF而是可以直接计算得到了。
3.3. 称谓的习惯
关于反射率、二向反射因子、二向反射率等称谓,不同书中、不同文献中、不同学者通常各有各的称谓,有时严格,有时不严格,造成很多人的混淆,这里我尝试澄清一下:
严格意义上讲,地物的总体反射率应该叫做反照率,描述地物的总的反射情况,忽略各个方向反射的空间分布特征。 绝大多数近地面测量或遥感观测都是在 天底 nadir方向的,大部分学者直接将天底方向观测到的BRF称为反射率,而不是严格称为反射因子。在多角度遥感观测中,很多学者直接将 方向 directional观测到的BRF称为方向反射率,而不是严格称为反射因子。所以大家在看文献和与人的交流中,要时刻提醒自己注意,对方的称呼到底指的是什么量。

3.4. 取值范围
写到这里,我们终于可以回答反射率、反射因子能不能大于1的问题了。
按照本文的严格定义与称谓,反射率的取值范围是0~1,是不可能大于1的。 比如反照率不可能大于1.
一些卫星遥感产品中所说的 反射率 reflectance,其实应该是二向反射率,更严格的称谓是二向反射因子。根据这个公式,是可以大于1的:例如,想象一个镜面,只有单一的反射方向,那么,于是有,因此BRF会很大。
近地面遥感中的单一方向测量,测得的都是反射因子,根据公式 ,如果,自然BRF取值大于1.
4. 结语
本篇博文的信息量很大,尤其是BRDF的定义和BRF的公式推导,一定要掌握。另外,一些乱七八糟的称谓也要大家时刻提醒自己区分。
我们用BRDF和BRF刻画了地物的二向性反射特征,但是其实这两者都是比较概念性的量:
非常非常严格意义上说,采用传感器是无法测量的,因为任何传感器都是有一个视场角的,这并不满足定义中的
方向-方向的描述,无法做到足够小的。另一方面,真实场景下,除了太阳直射光外,还有天空散射光,甚至临近地物的散射,都可能是的入射辐射, 因此:
入射是从半球空间入射的,需要其他的反射度量进行描述。
还有,有时我们希望对半球反射的总体情况也进行一下描述:
有的同学说了,反射率(或反照率)不就是描述半球反射的总体情况的吗?其实我们还希望更具体地描述直射入射、半球入射各自造成的半球反射的效果。
综上,我们需要更加细化地描述地物的各种入射方向(单一方向、半球方向)和各种反射方向(单一方向、半球方向)下的反射情况,考虑到一篇博文不要太长,容易疲倦,我在下篇博文中在进行讲解吧。