【算法】筛选法统计素数--埃拉托色尼筛

埃拉托色尼的筛子

生成素数有很多方法，本文介绍的算法是一种高效的筛选算法 ---埃拉托色尼筛选法。

比如，要产生[2,n] 范围内的所有素数，步骤如下：

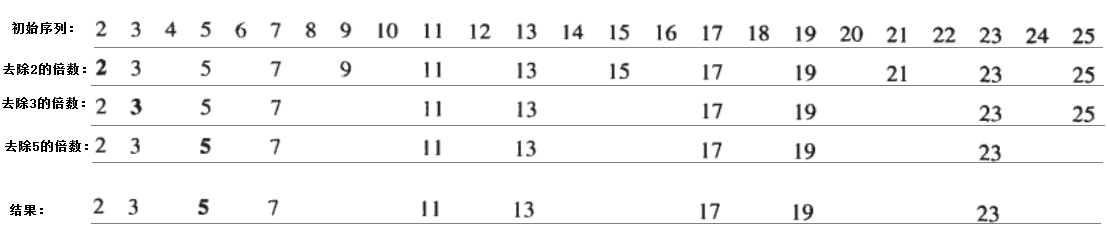
1、构造一个2,3,4,5,...n 的候选数序列 A 。

2、不断的去除（筛掉）序列A中的非素数。

     ①去掉2的倍数 。

     ②再去掉3的倍数。

     ③去掉4的倍数（不需要，因为在第一步已经被去掉了）  去掉5的倍数。

     ④去掉6的倍数

     ⑤去掉7 的倍数

        ... ...   一直到不能再去除为止。

3、经过反复的筛选去除后，序列A就只剩下了[2,n]内的素数

例子：产生[2,25]范围的素数序列

代码实现

/*
使用一个bool 数组。数组的下标代表待筛选的数，而用数组元素的值代表 数的存在与否。

如 A[p] = true  表示数p 存在，没有被去除。则p为素数

*/

void select_prime(int n)
{
    if (n < 2) return ;              
    
    const bool exist     = true;
    const bool not_exist = false;


    bool*A = new bool[n + 1];    //会浪费 数组的第一 和第二个元素空间.因为 0 和 1 既不是素数，也不是合数。
    memset(A, exist, sizeof(bool)*(n + 1));  //初始化为exist

    for (int p = 2; p*p <=n; p++)
    {
        if (A[p] == exist)         //
        {                          //
            int j = p*p;          //
            while (j <= n)        //
            {                     //
                A[j] = not_exist; //
                j += p;           // 
            }                     //
        }                         //
    }

    //至此 ，使得A[p]为true 的p都是素数。这里不再具体操作，取决于你自己的实现。如打印，或者转存

    delete[] A;

}

代码解读

整体代码，估计就是for循环那段代码可能不好理解。我们先分析for内部的代码。

if (A[p] == exist)        //如果p是素数
 {                        
      int j = p*p;   //则从p*p开始 去除
      while (j <= n)        
      {                     
           A[j] = not_exist;    //标记为   去除状态
           j += p;              //递增到下一个倍数
      }                     
}      

  

也就是说，对于一个数p，会依次去除  p*p  ,  p(p+1) , p(p+2) .... p(p+k)   【p(p+k)<=n】

前面不是说要去除 p 的所有倍数的吗？那 2p ,3p  4p ...p(p-1)怎么不去除呢？

他们已经被去除了。因为当前我们要消去 p 的倍数，那么，之前一定去除了 p-1 , p-2 ，p-3 ... 4 ， 3 ， 2  的这些数 的倍数，So ， p(p-1)  , p(p-2) .... p3  p2 显然在之前的操作中被去除。

也正是因为这个原因，最外面的for循环，p 的值从 2  到 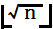  ，而不必从 2 到 n。为了避免使用sqrt函数带来消耗，我使用了乘法，是同样的效果。

即便通过技巧减少不必要的去除操作，上面的代码依然存在重复去除的可能。比如数字35，在去除5的倍数时被标记为  去除 ，在去除7的倍数时，也会再次被标记 。当然这不影响结果的正确性。但是如果要统计素数的个数，就需要小小的修改一下代码了。

统计素数的个数

int countPrime(int n)
{
    if (n < 2) return 0;

    const bool exist = true;
    const bool not_exist = false;

    unsigned  count = n - 1;      //假设全部是素数
    

    bool*A = new bool[n + 1];   
    memset(A, exist, sizeof(bool)*(n + 1));

    for (int p = 2; p*p <= n; p++)
    {
        if (A[p] == exist)
        {
            int j = p*p;
            while (j <= n)
            {
                if (A[j] == exist)     //只有没被去除，才做去除操作。避免重复统计
                {
                    A[j] = not_exist;
                    count--;           //减少1个
                }
                j += p;
            }
        }
    }


    delete[] A;

    return count;

}

这个算法的速度比我的这篇文章中最好的solution还要快10倍，很是强悍。但有个缺点就是空间复杂度为O(n)。

使用这个算法解决leetcode题目后的runtime统计，可以发现这个算法超越了98.89%的Ac。