算法的六种排序

一、选择排序法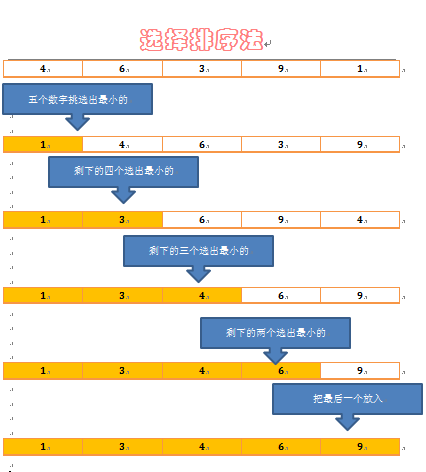

　　简单选择排序是最简单直观的一种算法，基本思想为每一趟从待排序的数据元素中选择最小（或最大）的一个元素作为首元素，直到所有元素排完为止，简单选择排序是不稳定排序。

　        for (int i = 0; i < arr.length - 1; i++) {

            int min = i;//每一趟循环比较时，min用于存放较小元素的数组下标，这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标，避免每次遇到较小元素都要进行交换。
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    min = j;
                }
            }
         }

　　简单选择排序通过上面优化之后，无论数组原始排列如何，比较次数是不变的；对于交换操作，在最好情况下也就是数组完全有序的时候，无需任何交换移动，在最差情况下，也就是数组倒序的时候，交换次数为n-1次。综合下来，时间复杂度为
)

二、冒泡排序
　　

　　冒泡排序的基本思想是，对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序

 for (int i = 0; i < arr.length - 1; i++) {
            boolean flag = true;//设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已然完成。
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr,j,j+1);
                    flag = false;
                }
            }
            if (flag) {
                break;
            }
        }

　　根据上面这种冒泡实现，若原数组本身就是有序的（这是最好情况），仅需n-1次比较就可完成；若是倒序，比较次数为 n-1+n-2+

^...

+1=n(n-1)/2，交换次数和比较次数等值。所以，其时间复杂度依然为O(n

²

）。综合来看，冒泡排序性能还还是稍差于上面那种选择排序的。
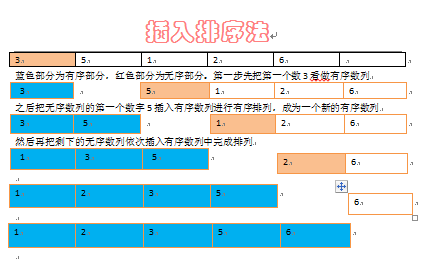
三、插入排序
　　直接插入排序基本思想是每一步将一个待排序的记录，插入到前面已经排好序的有序序列中去，直到插完所有元素为止。

for (int i = 1; i < arr.length; i++) {
            int j = i;
            while (j > 0 && arr[j] < arr[j - 1]) {
                swap(arr,j,j-1);
                j--;
            }
        }
 

　　简单插入排序在最好情况下，需要比较n-1次，无需交换元素，时间复杂度为O(n);在最坏情况下，时间复杂度依然为O(n²)。但是在数组元素随机排列的情况下，插入排序还是要优于上面两种排序的。

四、希尔排列

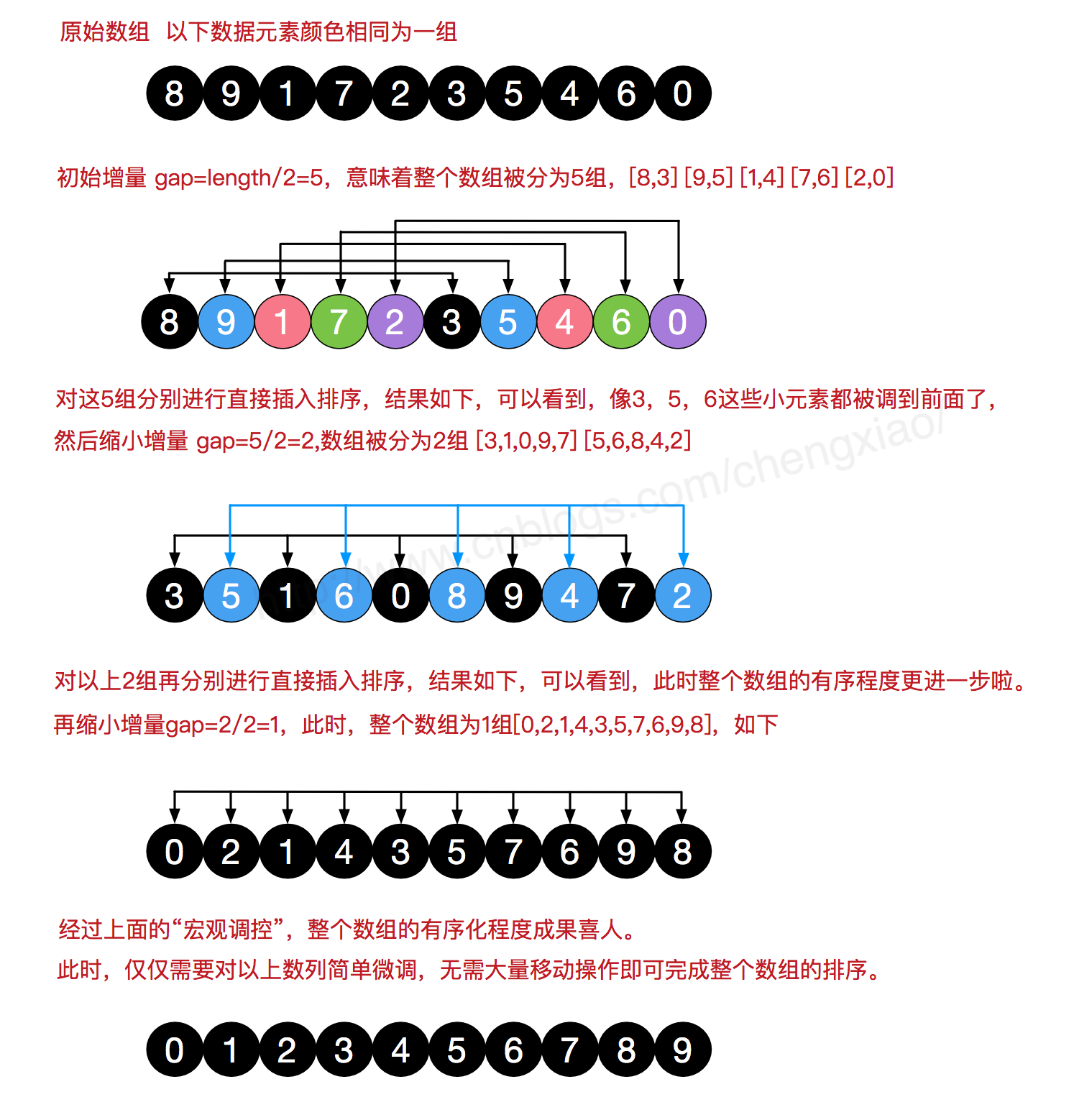
　　希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

public class ShellSort {
 9     public static void main(String []args){
10         int []arr ={1,4,2,7,9,8,3,6};
11         sort(arr);
12         System.out.println(Arrays.toString(arr));
13         int []arr1 ={1,4,2,7,9,8,3,6};
14         sort1(arr1);
15         System.out.println(Arrays.toString(arr1));
16     }
17 
18     /**
19      * 希尔排序 针对有序序列在插入时采用交换法
20      * @param arr
21      */
22     public static void sort(int []arr){
23         //增量gap，并逐步缩小增量
24        for(int gap=arr.length/2;gap>0;gap/=2){
25            //从第gap个元素，逐个对其所在组进行直接插入排序操作
26            for(int i=gap;i<arr.length;i++){
27                int j = i;
28                while(j-gap>=0 && arr[j]<arr[j-gap]){
29                    //插入排序采用交换法
30                    swap(arr,j,j-gap);
31                    j-=gap;
32                }
33            }
34        }
35     }
36 
37     /**
38      * 希尔排序 针对有序序列在插入时采用移动法。
39      * @param arr
40      */
41     public static void sort1(int []arr){
42         //增量gap，并逐步缩小增量
43         for(int gap=arr.length/2;gap>0;gap/=2){
44             //从第gap个元素，逐个对其所在组进行直接插入排序操作
45             for(int i=gap;i<arr.length;i++){
46                 int j = i;
47                 int temp = arr[j];
48                 if(arr[j]<arr[j-gap]){
49                     while(j-gap>=0 && temp<arr[j-gap]){
50                         //移动法
51                         arr[j] = arr[j-gap];
52                         j-=gap;
53                     }
54                     arr[j] = temp;
55                 }
56             }
57         }
58     }
59     /**
60      * 交换数组元素
61      * @param arr
62      * @param a
63      * @param b
64      */
65     public static void swap(int []arr,int a,int b){
66         arr[a] = arr[a]+arr[b];
67         arr[b] = arr[a]-arr[b];
68         arr[a] = arr[a]-arr[b];
69     }
70 }