问题描述:
数据结构之并查集
问题解决:
(1)概述
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。 进行快速规整。
(2)基本操作
合并两个不相交集合
判断两个元素是否属于同一集合
主要操作的解释及代码
需要注意的是,一开始我们假设元素都是分别属于一个独立的集合里的。
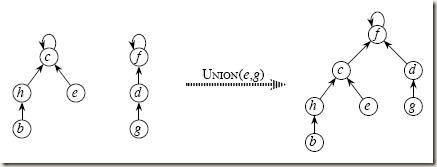
(1) 合并两个不相交集合 操作很简单:先设置一个数组Father[x],表示x的“父亲”的编号。 那么,合并两个不相交集合的方法就是,找到其中一个集合最父亲的父亲(也就是最久远的祖先),将另外一个集合的最久远的祖先的父亲指向它。
a图为两个不相交集合,b图为合并后Father(b):=Father(g)
代码C:
(2) 判断两个元素是否属于同一集合 仍然使用上面的数组。则本操作即可转换为寻找两个元素的最久远祖先是否相同。可以采用递归实现。
代码C:
(3)并查集优化
(3. 1)路径压缩
刚才我们说过,寻找祖先时采用递归,但是一旦元素一多起来,或退化成一条链,每次GetFather都将会使用O(n)的复杂度,这显然不是我们想要的。
对此,我们必须要进行路径压缩,即我们找到最久远的祖先时“顺便”把它的子孙直接连接到它上面。这就是路径压缩了。使用路径压缩的代码如下,时间复杂度基本可以认为是常数的。
附图摘自CLRS:
代码C:
(3. 2)rank合并
合并时将元素少的集合合并到元素多的集合中。
代码C:
时间复杂度:
完整代码实现:
参考资料:
http://www.nocow.cn/index.php/%E5%B9%B6%E6%9F%A5%E9%9B%86