声明:本文用到的代码均来自于PRTools(http://www.prtools.org)模式识别工具箱,并以matlab软件进行实验。
(1)在介绍Bagging和Boosting算法之前,首先要简单了解什么是集成学习?
集成学习(Ensemble Learning)是目前模式识别与机器学习中常用的一种学习算法,是使用一系列的学习器(分类器)通过某种规则(投票法、加权投票等)将各分类器的学习结果进行融合,达到比单学习器识别效果更好地目的。
可以打一个简单的比喻,如果我们将“学习器”看做是一个“人”,现在我们需要进行的任务是识别汉字。一个人的识别内容终归是有限的,但是如果我们现在利用三个人来识别,同一个字当A识别错误时,B、C识别正确,最终以少数服从多数的原则取BC的识别结果,那么相比较只用A一个人来识别汉字的情况,我们的准确率会大大提升。当然也许这里有人会存在疑问:万一A本身是一个很有文化的人,B是一个不识字的人,那么叫他们两个一起识别汉字岂不是会拉低整体识别率么?这里也就牵扯到了学习器与学习器之间差异性度量的话题,这个话题在本文中不详细讲述,有兴趣的朋友可以自己查询了解,最白话的解释就是:参与集成学习的学习器们需要具有一定的差异值,既不能完全相同,也不能差异的太大。
在浅显的理解何为集成学习之后,我们来讲Bagging和Boosting,事实上这是两种非常重要的集成方法。
(2)Bagging
该算法在模式识别工具箱中的使用方法为:
W = baggingc (A,CLASSF,N,ACLASSF,T) INPUT A Training dataset. CLASSF The base classifier (default: nmc) N Number of base classifiers to train (default: 100) ACLASSF Aggregating classifier (default: meanc), [] for no aggregation. T Tuning set on which ACLASSF is trained (default: [], meaning use A) OUTPUT W A combined classifier (if ACLASSF was given) or a stacked classifier (if ACLASSF was []).
以上是PRtools工具箱中bagging的使用说明。
其中:A是训练数据集,其类型是dataset。
CLASSF是基学习器的训练算法,该工具箱中涵盖多种分类器的算法,比较常用的有nmc(最近邻)、treec(决策树)等等。
N是学习器数目,即要训练多少个分类器做最终的集成,默认值100.
ACLASSF是指集成规则,可选的参数有meancprodcmediancmaxcmincvotec,其中默认参数为meanc,但是比较常用的规则还是votec投票法
T是指训练集成规则的参数,像投票法是不需要训练的,因为默认该值为[]。
以上内容是直接从工具箱中bagging方法的应用角度来介绍,接下来要从原理方面讲述。
Bagging算法的全称应该是Bootstrap aggregating。
它有两个步骤组成:Bootstrap和aggregating。
所谓基分类器,指的是参与集成的个体分类器,某一种分类算法加以实现后(可以理解为一个函数,输入是特征数据,输出是判断的类别)就是一个分类器。
Boostrap方法是有放回的抽样,即从初始训练集中有放回可重复的随机取出N条数据(这个值需要事先设定,可以是初始数据集的80%、70%都随意)组成新的数据集,假如我们现在要训练100个分类器,那么就取出100组数据集分别进行训练,即要训练100轮。因为每次训练的数据集是不同的,所以训练出的分类器也存在差异。这样我们就得到了100个预测函数序列h1,…,h100。
另一个步骤就是集成,通常用的是投票法。
因此这里主要记住的就是Bagging中分类器的生成方式,当然训练分类器的算法往往有稳定和不稳定两类,通常是使用不稳定的学习算法,因为不稳定的学习算法可以因为数据集微小的变化而导致结果的改变,因此有助于我们生成若干具有一定差异性的分类器集合。
一个例子:
在二维数据中,使用不同的训练算法时的集成效果
clc,clear; A=gendath([50 50]); [C,D]=gendat(A,[20 20]); W1=baggingc(C,qdc); %quadratic W2=baggingc(C,ldc); %linear W3=baggingc(C,knnc); W4=baggingc(C,treec); disp([testc(D*W1), testc(D*W2), testc(D*W3), testc(D*W4)]); scatterd(A); plotc({W1,W2,W3,W4 });
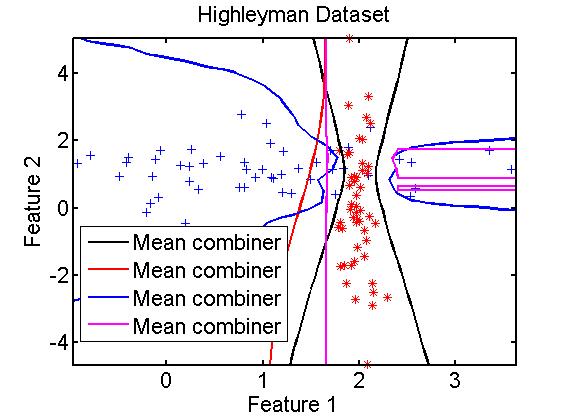
(3)Boosting
该算法在模式识别工具箱中的使用方法为:
[W,V,ALF] = adaboostc(A,CLASSF,N,RULE,VERBOSE); INPUT A Dataset CLASSF Untrained weak classifier N Number of classifiers to be trained RULE Combining rule (default: weighted voting) VERBOSE Suppress progress report if 0 (default) OUTPUT W Combined trained classifier V Cell array of all classifiers Use VC = stacked(V) for combining ALF Weights
其参数多数和baggingc很像:
A是训练数据集,其类型是dataset。
CLASSF是基学习器的训练算法。
N是学习器数目。
ACLASSF是指集成规则,其中默认参数为加权投票法。
Boosting主要是Adaboost(Adaptive Boosting),它与Bagging的不同在于他将权重赋予每个训练元组,生成基分类器的过程为迭代生成。每当训练生成一个分类器M(i)时要进行权重更新,使得M(i+1)更关注被M(i)分类错误的训练元组。最终提升整体集合的分类准确率,集成规则是加权投票,每个分类器投票的权重是其准确率的函数。
继续详细介绍的话,假设数据集D,共有d类。(X1,Y1)…(Xd,Yd),Yi是Xi的类标号,假设需要生成k的分类器。其步骤为:
1、对每个训练元组赋予相等的权重1/d。
2、for i=1:k
从D中进行有放回的抽样,组成大小为d的训练集Di,同一个元组可以被多次选择,而每个元组被选中的几率由权重决定。利用Di训练得到分类器Mi,然后使用Di作为测试集计算Mi的误差。然后根据误差调整权重。
当元组没有被正确分类时,则权重增加;反之权重减少。然后利用新的权重为下一轮训练分类器产生训练样本。使其更“关注”上一轮中错分的元组。
3、进行加权投票集成
一个例子:
clc,clear; A=gendath([50 50]); [C,D]=gendat(A,[20 20]); [W1,V1,ALF1]=adaboostc(C,qdc,100); %quadratic [W2,V2,ALF2]= adaboostc (C,ldc,100); %linear disp([testc(D*W1), testc(D*W2)]); scatterd(A); plotc({W1,W2});
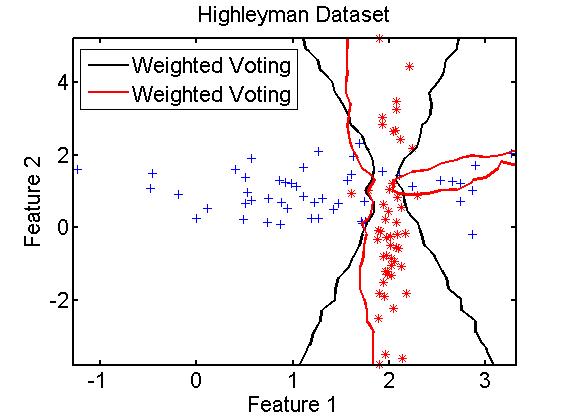
(3)Bagging与Boosting的差异
通过上述简单的介绍,可以看出这两种集成算法主要区别在于“加没加权”。Bagging的训练集是随机生成,分类器相互独立;而Boosting的分类器是迭代生成,更关注上一轮的错分元组。因此Bagging的各个预测函数可以并行生成;而Boosting只能顺序生成。因此对于像一些比较耗时的分类器训练算法(如神经网络等)如果使用Bagging可以极大地解约时间开销。
但是通过在大多数数据集的实验,Boosting的准确率多数会高于Bagging,但是也有极个别数据集使用Boosting反倒会退化。
本文没有对两种集成方法的背景知识做过多的介绍,主要是结合模式识别工具箱的应用来简单作为了解使用,如有不准确的地方,还望多加指正。