矩阵相乘：lapack dgemm 效率

lapack 的 dgemm 函数可以用来进行矩阵相乘，我要在 c++ 中调用，把它进行了封装。另外我手写了一个矩阵相乘函数，用来进行效率对比，看看 dgemm 比我手写的快多少倍。代码如下：

#include<iostream>
using namespace std;
#include<fstream>
#include<cmath>
#include<stdlib.h>
#include<vector>

extern "C" void dgemm_(char *TRANSA, char *TRANSB, int *M, int *N, int *K, double* ALPHA, double *A, int* LDA, double *B, int* LDB, double* BETA, double *C, int* LDC);

/*
 * wraps dgemm_() in lapack, uses one of the optional modes of it to do C := A B
 * int n                dimension
 * double * A           A[ n*n ]
 * double * B           B[ n*n ]
 * double * C           C[ n*n ]
 */
void lapack_dgemm( int n, double * A, double * B, double * C ){

        // dgemm (... ) : C = alpha * op( A ) * op( B ) + beta * C
        char TRANSA='N'; // op( A ) = A
        char TRANSB='N'; // op( B ) = B
        int M=n; // number of rows in A
        int N=n; // number of columns in B
        int K=n; // number of columns in A, also equals number of rows in B
        double ALPHA=1.0; // alpha
        double BETA=0.0; // beta
        int LDA=n; // leading dimension of A
        int LDB=n; // leading dimension of B
        int LDC=n; // leading dimension of C

        dgemm_(&TRANSA, &TRANSB, &M, &N, &K, &ALPHA, B, &LDA, A, &LDB, &BETA, C, &LDC);
        // because dgemm is written in fortran, it actually gets B^	op A^	op = ( AB )^	op, an (AB)^	op will actually be stored in fortran manner, that is AB in C++
}

void mtx_multiply( int n, double * A, double * B, double * C ){
        double y;
        for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                        y = 0;
                        for(int k=0;k<n;k++) y += A[i*n+k] * B[k*n+j];
                        C[i*n+j] = y;
                }
        }
};

int main(){

        /*
        // test: A = [ 0, 1, 0, 0 ], B = [ 0, 1, -1, 0 ]
        // AB = [ -1, 0, 0, 0 ], A^T B^T = [ 0, 0, 0, -1 ]
        int n = 2;
        double A[4] = { 0, 1, 0, 0 };
        double B[4] = { 0, 1, -1, 0 };
        double C[4];

        lapack_dgemm( n, A, B, C );

        cout<<"C: "; for(int i=0;i<4;i++) cout<<C[i]<<","; cout<<endl;
        */

        vector<int> dim = {10, 20, 30, 40, 50, 100, 200, 500, 800, 1000 };
        vector<double> t_lapack;
        vector<double> t_handwritten;

        for(auto n : dim ){
                cout<<" n = "<<n<<endl;
                double * A = new double [ n*n ];
                for(int i=0;i<n*n;i++) A[i] = ((double)rand())/RAND_MAX;
                double * B = new double [ n*n ];
                for(int i=0;i<n*n;i++) B[i] = ((double)rand())/RAND_MAX;
                double * C = new double [ n*n ];

                clock_t t1 = clock();
                lapack_dgemm( n, A, B, C );
                time_t t2 = clock();
                cout<<" lapack dgemm:  " << (double)(t2-t1)/CLOCKS_PER_SEC <<" s."<<endl;
                t_lapack.push_back( (double)(t2-t1)/CLOCKS_PER_SEC );

                mtx_multiply( n, A, B, C );
                time_t t3 = clock();
                cout<<" hand written: " << (double)(t3-t2)/CLOCKS_PER_SEC << " s."<<endl;
                t_handwritten.push_back( (double)(t3-t2)/CLOCKS_PER_SEC );

                delete [] A; delete [] B; delete [] C;
        }

        cout<<" t_lapack: "; for(auto t : t_lapack) cout<<t<<", "; cout<<endl;
        cout<<" t_handwritten: "; for(auto t : t_handwritten) cout<<t<<", "; cout<<endl;

        return 0;
}

得到的结果用python画图：

import numpy as np
import matplotlib.pyplot as plt

n = np.array([ 10, 20, 30, 40, 50, 100, 200, 500, 800, 1000 ])
t1 = np.array([ 3.8e-05, 3.1e-05, 7.8e-05, 0.000232, 0.000308, 0.002722, 0.003365, 0.050828, 0.194913, 0.405148 ])
t2 = np.array([ 7e-05, 0.000112, 0.000409, 0.000798, 0.001467, 0.005489, 0.018586, 0.324087, 1.56575, 2.9442 ])
plt.plot(n,t1, label="dgemm")
plt.plot(n,t2, label="handwritten")
plt.plot(n,t2/t1, label="speedup")
plt.legend(loc=0)
#plt.ylim(-0.5,11)
plt.xlabel("dimension",fontsize=15)
plt.ylabel("t(s)", fontsize=15)

得到图片：

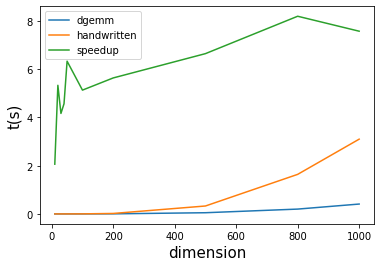
所以可以说，dgemm比手写的代码要快 2-8倍，矩阵维数 n = 30 - 40 时，能快 4-5 倍。