BZOJ2693：JZPTAP——题解

http://www.lydsy.com/JudgeOnline/problem.php?id=2693

Description

 

Input

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

1
4 5

Sample Output

122

——————————————————————————————————————————

图片和题解参考均来自于https://www.cnblogs.com/GXZlegend/p/7000042.html以其这里面的链接。

推导过程如图：

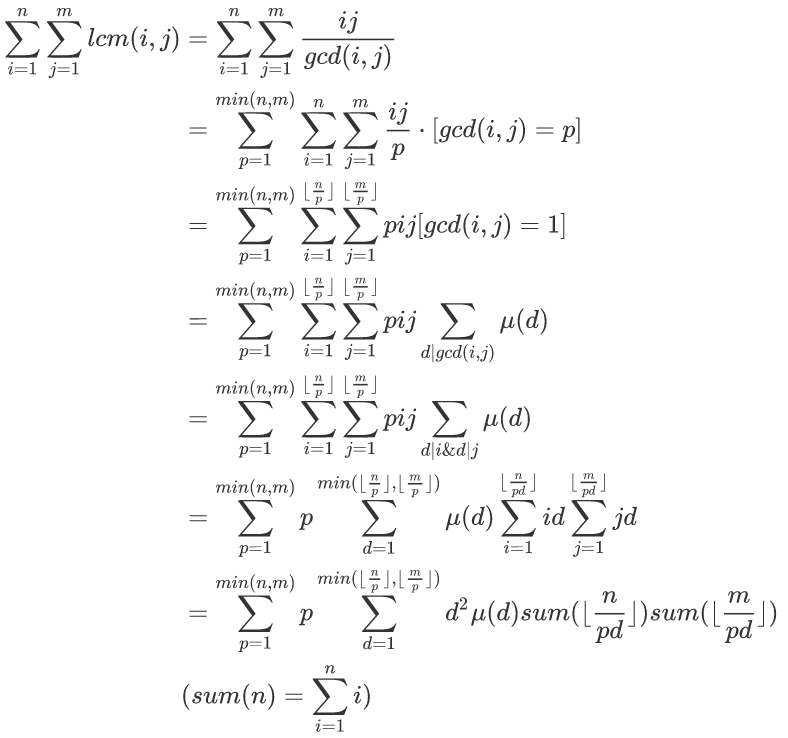
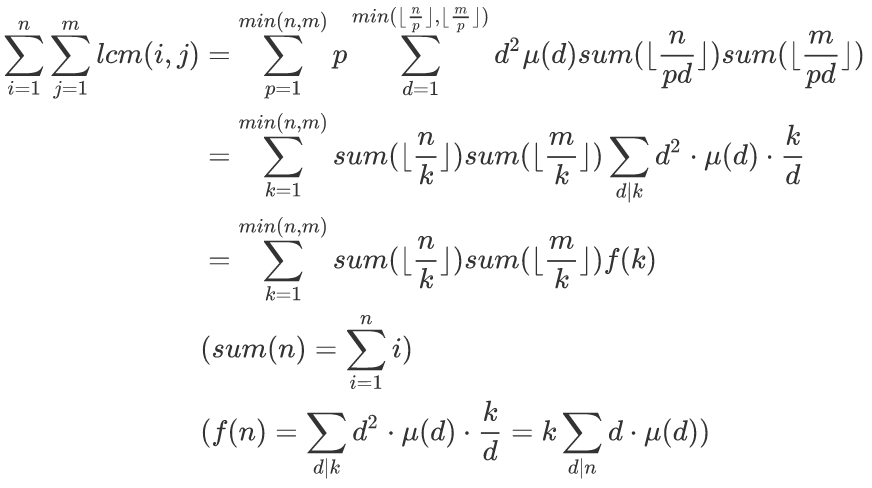
这里说一下比较不好理解的步骤。

将每一行边号从1开始。

2：只是变成了枚举gcd的取值，然后判断是否应该取即可。

3：i变成了i/p之后自然需要乘p*p，一约分就成了3式子。

以及最后一个fn当中的所有k应当为n。

然后引用上面的博客来求fn：

设f1(n)=n²mu(n)，f2(n)=n，则显然f2是积性函数，f1为两个积性函数的乘积，也是积性函数。

那么f为f1和f2的狄利克雷卷积，也是积性函数。

所以可以尝试快筛f(n)。

当n为质数时，显然f(n)=n-n^2。

当n不为质数时，即n=i*p，p|i，p是质数，那么观察f(n)化简之后的式子，n新增加出来的约数一定是包含p^2的，它的mu值一定是0，所以f(n)的改变只是从i*...变为了n*...，所以此时f(n)=f(i)*p。

#include<cstdio>
#include<queue>
#include<cctype>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=10000010;
const int p=1e8+9;
inline int read(){
    int X=0;char ch=0;
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return X;
}
ll f[N],su[N];
bool he[N];
inline ll s(ll x){
    return x*(x+1)/2%p;
}
void Euler(int n){
    int tot=0;
    f[1]=1;    
    for(int i=2;i<=n;i++){
    if(!he[i]){
        su[++tot]=i;
        f[i]=(ll)((i-(ll)i*i)%p+p)%p;
    }
    for(int j=1;j<=tot;j++){
        if(i*su[j]>n)break;
        he[i*su[j]]=1;
        if(i%su[j]==0){
        f[i*su[j]]=f[i]*su[j]%p;
        break;
        }
        else f[i*su[j]]=f[i]*f[su[j]]%p;
    }
    }
    for(int i=1;i<=n;i++){
    f[i]+=f[i-1];
    if(f[i]>=p)f[i]-=p;
    }
    return;
}   
int main(){
    Euler(10000000);
    int t=read();
    while(t--){
    int n=read(),m=read(),ans=0;
    if(n>m)swap(n,m);
    for(int i=1,j;i<=n;i=j+1){
        j=min(n/(n/i),m/(m/i));
        ans+=(ll)(f[j]-f[i-1])*s(n/i)%p*s(m/i)%p;
        if(ans<0)ans+=p;
        if(ans>=p)ans-=p;
    }
    printf("%d
",ans);
    }
    return 0;
}