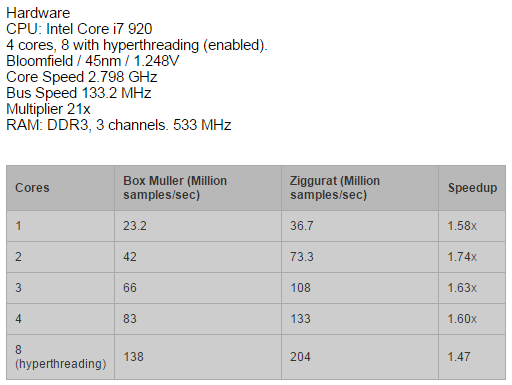
1. Ziggurat 算法与 Box-muller 算法的效率比较
2. Box-Muller
a. 一般形式 因函数调用较多,速度慢,当u接近0时存在数值稳定性问题
先假设。
用Box-Muller方法,随机抽出两个从均匀分布的数字
和
。然后
那和
都是正态分布的。
证明可用极坐标,请参考教科书中的Box-Muller方法。
另外使用反函数,先随机抽出一个从均匀分布的数字
,然后
那是正态分布的。
b.极坐标形式,速度快且有更好的数值鲁棒性
double pf_ran_gaussian(double sigma)
{
double x1, x2, w, r;
do
{
do { r = drand48(); } while (r==0.0);
x1 = 2.0 * r - 1.0;
do { r = drand48(); } while (r==0.0);
x2 = 2.0 * r - 1.0;
w = x1*x1 + x2*x2;
} while(w > 1.0 || w == 0.0);
return(sigma * x2 * sqrt(-2.0*log(w)/w));
}
3. zigurat 方法
Box–Muller 算法虽然非常快,但是由于用到了三角函数和对数函数,相对来说还是比较耗时的,如果想要更快一点有没有办法呢?
当然有,这就是 Ziggurat 算法,不仅可以用于快速生成正态分布,还可以生成指数分布等等。Ziggurat 算法的基本思想是利用拒绝采样,什么是拒绝采样呢?
拒绝采样(Rejection Sampling),有的时候也称接收 - 拒绝采样,使用场景是有些函数p(x)
太复杂在程序中没法直接采样,那么可以设定一个程序可抽样的分布q(x)比如正态分布等等,然后按照一定的方法拒绝某些样本,达到接近p(x)
分布的目的:
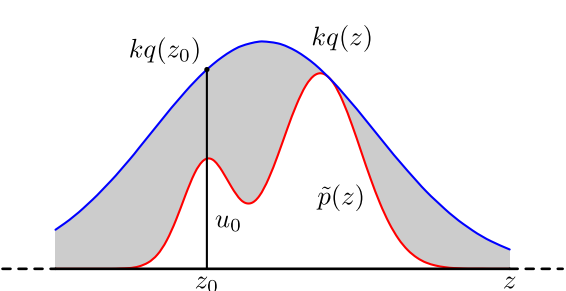
具体操作如下,设定一个方便抽样的函数 $q(x)$,以及一个常量 $k$,使得 $p(x)$ 总在 $kq(x)$ 的下方。(参考上图)
- x轴方向:从q(x)分布抽样得到a
- y轴方向:从均匀分布(0,kq(a))中抽样得到u
- 如果刚好落到灰色区域:u>p(a),拒绝;否则接受这次抽样
- 重复以上过程
证明过程就不细说了,知道怎么用就行了,感兴趣的可以看看这个文档
不过在高维的情况下,拒绝采样会出现两个问题,第一是合适的 $q$ 分布比较难以找到,第二是很难确定一个合理的 $k$ 值。这两个问题会造成图中灰色区域的面积变大,从而导致拒绝率很高,无用计算增加。
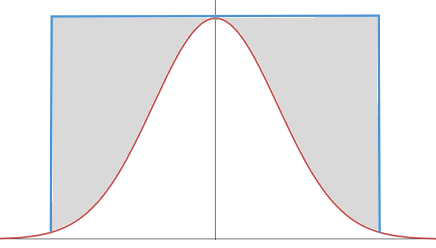
采用拒绝采样来生成正态分布,最简单直观的方法莫过于用均匀分布作为 $q(x)$,但是这样的话,矩形与正态分布曲线间的距离很大,就会出现刚才提到的问题,高效也就无从谈起了。
而 Ziggurat 算法高效的秘密在于构造了一个非常精妙的q(x),看下面这张图
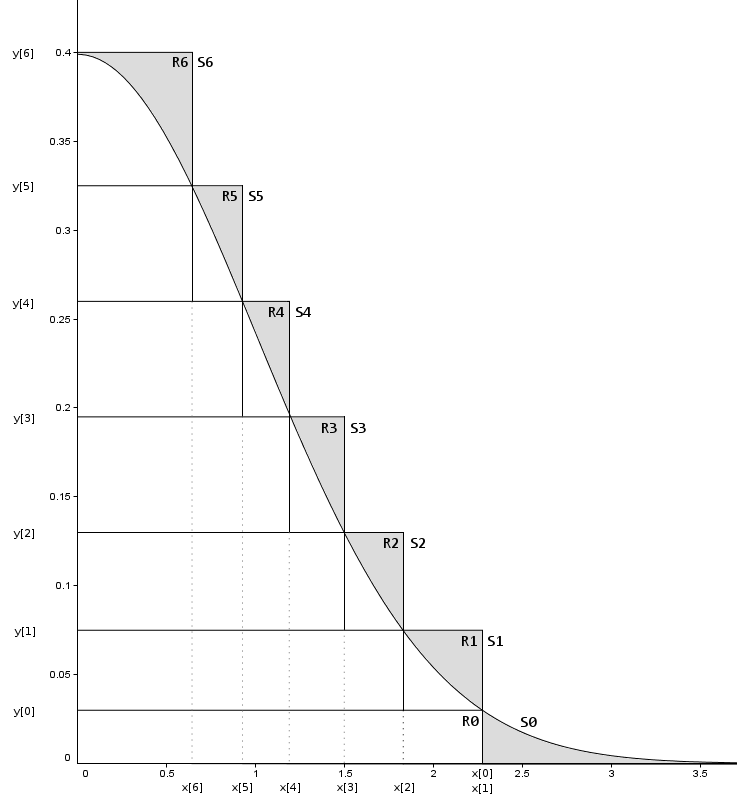
我们用多个堆叠在一起的矩形,这样保证阴影部分(被拒绝部分)的始终较小,这样就非常高效了
简单对图作一个解释:
- 我们用
R[i]来表示一个矩形,R[i]的右边界为x[i],上边界为y[i]。S[i]表示一个分割,当i=0时,S[0]=R[0]+tail,其他情况S[i]==R[i] - 除了
R[0]以外,其他每个矩形面积相等,设为定值A。R[0]的面积 = A-tail的面积。这样保证从任何一个分割中抽样(x,y)的概率相等 - 当任意选定一个
R[i]在其中抽样(x,y),若x<x[i+1],y必然在曲线下方,满足条件,接受x;若x[i+1]<x<x[i],则还需要进一步判断。同样这里R[0]和tail中的样本需要进行特殊处理 - 这里为了方便解释,只用了几个矩形,在程序实现的时候,一般使用
128或256个矩形
可以看出,为了提高效率,Ziggurat 算法中使用了许多技巧性的东西,这在其C代码实现中更加明显,使用了与运算和字节等各种小技巧,代码就不在这里贴了,感兴趣可以看看下面几个版本,C版本的追求的是极致的速度,每个矩形的边界已经提前计算好了。C#版本中的注释非常详细,Java版的基本与C#一致,但是效率一般。
4. 总结
Box-muller 算法应对一般的需求足够了,但是要生成大量服从正态分布的随机数时,Ziggurat 算法效率会更高一点。
参考: https://www.taygeta.com/random/gaussian.html // Box-Muller的介绍
https://cosx.org/2015/06/generating-normal-distr-variates // 对比介绍
https://www.zhihu.com/question/29971598