1、卷积
下面给出一个具体的例子:假设你已经从一个 96x96 的图像中学习到了它的一个 8x8 的样本所具有的特征,假设这是由有 100 个隐含单元的自编码完成的。为了得到卷积特征,需要对 96x96 的图像的每个 8x8 的小块图像区域都进行卷积运算。也就是说,抽取 8x8 的小块区域,并且从起始坐标开始依次标记为(1,1),(1,2),...,一直到(89,89),然后对抽取的区域逐个运行训练过的稀疏自编码来得到特征的激活值。在这个例子里,显然可以得到 100 个集合,每个集合含有 89x89 个卷积特征。
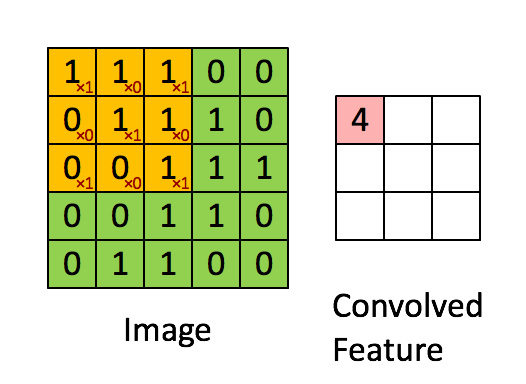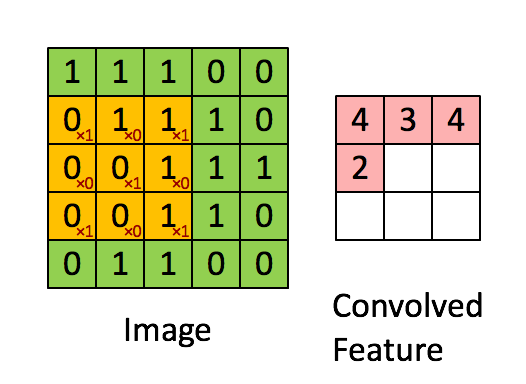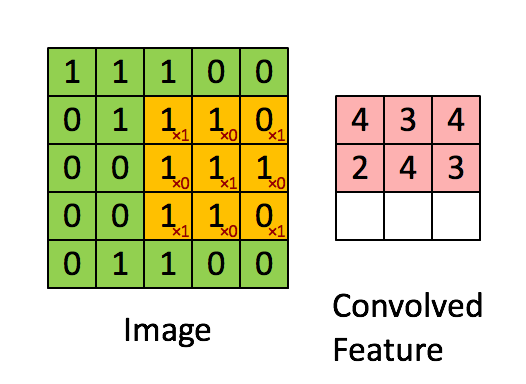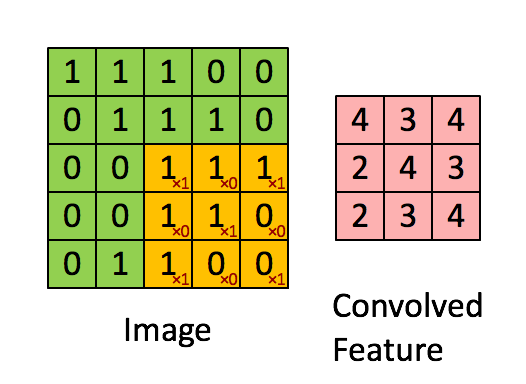
如下图所示,展示了一个3×3的卷积核在5×5的图像上做卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。
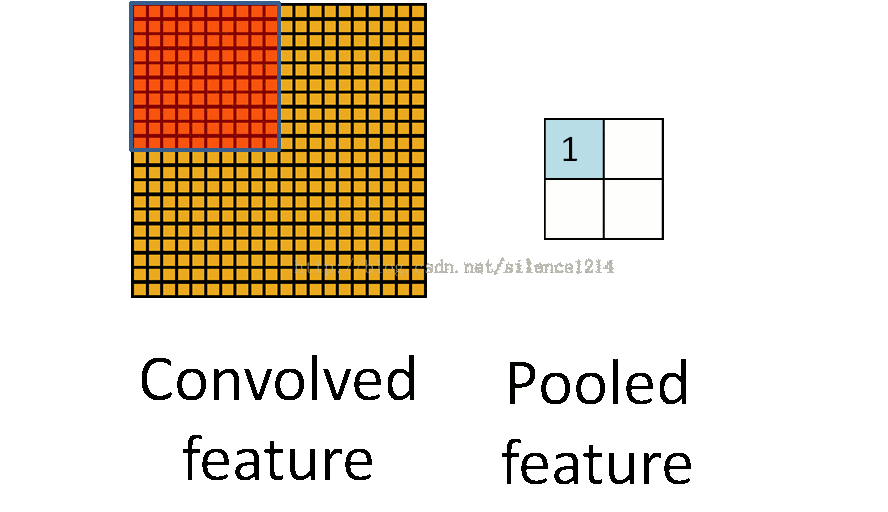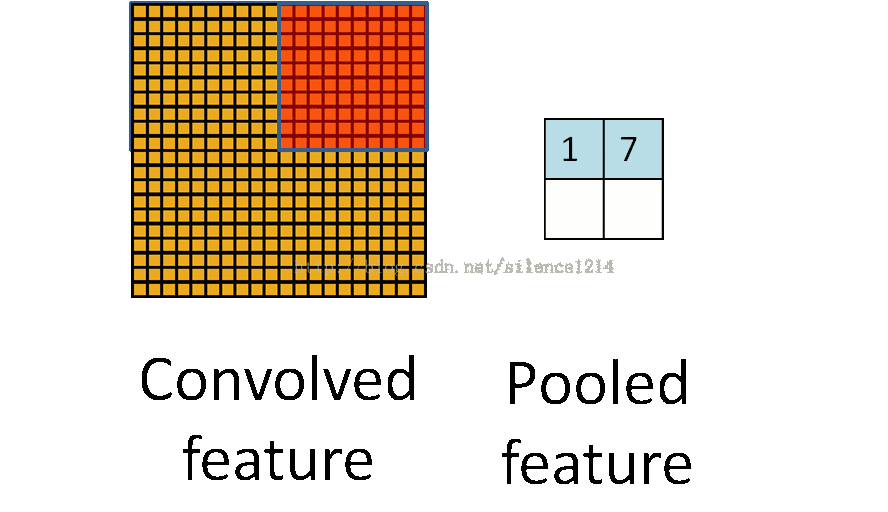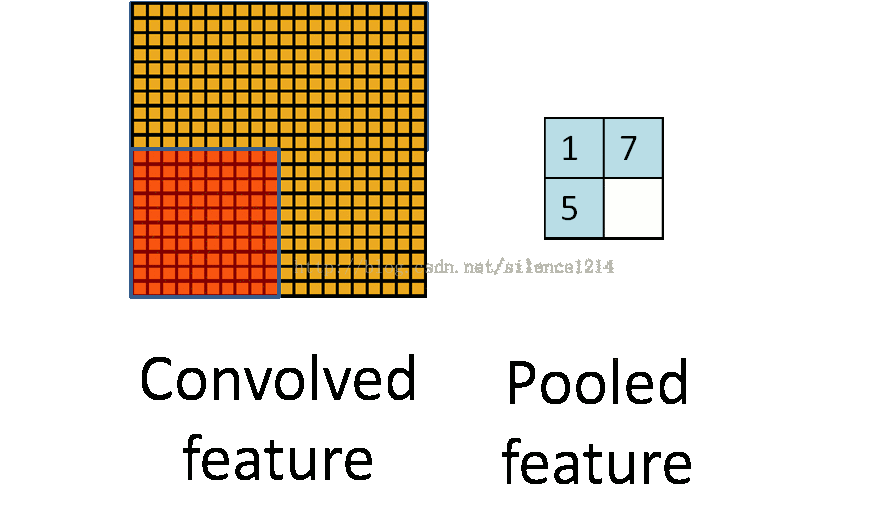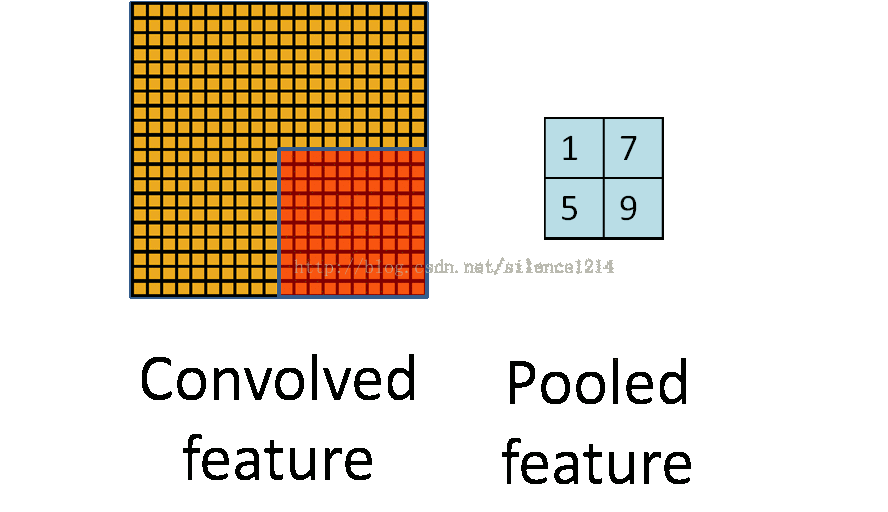
2:说下池化,其实池化很容易理解,先看图:
转自: http://blog.csdn.net/silence1214/article/details/11809947
比如上方左侧矩阵A是20*20的矩阵要进行大小为10*10的池化,那么左侧图中的红色就是10*10的大小,对应到右侧的矩阵,右侧每个元素的值,是左侧红色矩阵每个元素的值得和再处于红色矩阵的元素个数,也就是平均值形式的池化。
3:上面说了下卷积和池化,再说下计算中需要注意到的。在代码中使用的是彩色图,彩色图有3个通道,那么对于每一个通道来说要单独进行卷积和池化,有一个地方尤其是进行卷积的时候要注意到,隐藏层的每一个值是对应到一幅图的3个通道穿起来的,所以分3个通道进行卷积之后要加起来,正好才能对应到一个隐藏层的神经元上,也就是一个feature上去。
图像的上采样(upsampling)与下采样(subsampled)
缩小图像(或称为下采样(subsampled)或降采样(downsampled))的主要目的有两个:
1、使得图像符合显示区域的大小;2、生成对应图像的缩略图。
放大图像(或称为上采样(upsampling)或图像插值(interpolating))的主要目的是:
放大原图像,从而可以显示在更高分辨率的显示设备上。对图像的缩放操作并不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。然而,确实有一些缩放方法能够增加图像的信息,从而使得缩放后的图像质量超过原图质量的。
下采样原理:对于一幅图像I尺寸为M*N,对其进行s倍下采样,即得到(M/s)*(N/s)尺寸的得分辨率图像,当然s应该是M和N的公约数才行,如果考虑的是矩阵形式的图像,就是把原始图像s*s窗口内的图像变成一个像素,这个像素点的值就是窗口内所有像素的均值:
上采样原理:图像放大几乎都是采用内插值方法,即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。
无论缩放图像(下采样)还是放大图像(上采样),采样方式有很多种。如最近邻插值,双线性插值,均值插值,中值插值等方法。在AlexNet中就使用了较合适的插值方法。各种插值方法都有各自的优缺点。