个人作业1——四则运算题目生成程序（基于控制台）

1.分析与设计

a.题目要求: 

    写一个能自动生成小学四则运算题目的命令行 “软件”，满足以下需求：

1. 除了整数以外，还要支持真分数的四则运算，真分数的运算，例如：1/6 + 1/8 = 7/24
2. 运算符为 +, −, ×, ÷
3. 并且要求能处理用户的输入，并判断对错，打分统计正确率。
4. 要求能处理用户输入的真分数， 如 1/2, 5/12 等
5. 使用 -n 参数控制生成题目的个数，例如执行下面命令将生成10个题目
   Myapp.exe -n 10

b.需求分析: 

    能够自动生成小学生加减乘除四则运算题目，包括整数和真分数的运算。其需求包括：（1）能够控制生成题目的个数。（2）判断对错并统计正确率。

c.功能设计：

    1.基本功能：实现基本的加减乘除四则运算。

    2.扩展功能：能够处理真分数的四则运算。

    3.高级功能：判断对错并统计正确率。

 d.设计实现: 

    1.本实验采用java语言。

    2.程序包含三个类：（1）Fraction：包括mole、deno两个属性，分别是构成分数的分子和分母。

                                  （2）Calculate：包括FraAdd、FraSub、FraMul、FraDiv 四个方法，实现加、减、乘、除四则运算；

                                                         以及FraSim和Gcd两个方法，实现分数的化简及最大公约数的计算

                                  （3）Test：主函数。可以根据输入的n，生成相应的题数；

                                                 获取用户的answer，通过与正确答案的比较，判断对错，用right记录。

e.代码说明: 

    求最大公约数：

	public int Gcd(int a, int b) {
		int temp, r;
		if (a < b) {
			temp = a;
			a = b;
			b = temp;
		}
		while (b != 0) {
			r = a % b;
			a = b;
			b = r;
		}
		return a;
	}
}

    分数化简：　　

    public Fraction FraSim(Fraction f) {
        int gcd = Gcd(f.deno, f.mole);
        f.deno /= gcd;
        f.mole /= gcd;
        return f;
    }

    整数运算：

				sign = ran.nextInt(4);
				a = ran.nextInt(100);
				b = ran.nextInt(100);
				System.out.print(a);
				switch (sign) {
				case 0:
					IntRes = a + b;
					System.out.print("+");
					break;
				case 1:
					IntRes = a - b;
					System.out.print("-");
					break;
				case 2:
					IntRes = a * b;
					System.out.print("*");
					break;
				case 3:
					IntRes = a / b;
					System.out.print("/");
					break;
				}
				System.out.print(b + "=");
				answer = sc.nextInt();
				if (answer == IntRes) {
					right++;
				}

　　分数运算：

				sign = ran.nextInt(4);
				f1.deno = ran.nextInt(50) + 1;
				f1.mole = ran.nextInt(50);
				f2.deno = ran.nextInt(50) + 1;
				f2.mole = ran.nextInt(50);
				System.out.print(f1.mole + "/" + f1.deno);
				switch (sign) {
				case 0:
					FraRes = cal.FraAdd(f1, f2);
					System.out.print("+");
					break;
				case 1:
					FraRes = cal.FraSub(f1, f2);
					System.out.print("-");
					break;
				case 2:
					FraRes = cal.FraMul(f1, f2);
					System.out.print("*");
					break;
				case 3:
					FraRes = cal.FraDiv(f1, f2);
					System.out.print("/");
					break;
				}
				System.out.print(f2.mole + "/" + f2.deno + "=");
				FraAns = sc.next();
				fras = FraAns.split("/");
				FraM = Integer.parseInt(fras[0]);
				FraD = Integer.parseInt(fras[1]);
				if (FraM == FraRes.mole && FraD == FraRes.deno) {
					right++;
				}

f.测试运行: 

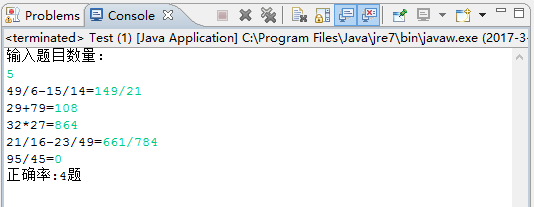
2.展示psp 

PSP2.1	Personal Software Process Stages	Time (h) Senior Student	Time (h)
Planning	计划	1	1.5
Estimate	估计这个任务需要多少时间	10	13
Analysis	需求分析 (包括学习新技术)	0.5	1
Coding Standard	代码规范	2	1.5
Design	具体设计	2	3
Coding	具体编码	5	6
Test	测试（自我测试，修改代码，提交修改）	1	2
Reporting	报告	1	1.5

3.小结

a.在实验过程中，由于java知识的遗忘，导致时常需要查阅资料，用时过长，需多加巩固练习。 

b.在实验主要遇到的问题是随机数的生成，后采用Random类的nextInt()方法获取。

c.在生成题目时，将整数和分数分成两种类型运算，导致无法进行整数与分数的计算。

d.在用户输入中，没有进行异常的处理，还需加强完善。

e.通过本次实验，进一步提升了我在编程中分析问题，解决问题的能力，希望有今后的实验中有更多的进步。

4.具体代码

https://git.coding.net/byc-xiong/test1.git