刘勇 Email:lyssym@sina.com
简介
鉴于维特比算法可解决多步骤中每步多选择模型的最优选择问题,本文简要介绍了维特比算法的基本理论,并从源代码角度对维特比算法进行剖析,并对源码中涉及的要点进行了解读,以便能快速应用该算法解决自然语言处理中的问题。
理论
维特比算法是一个特殊但应用最广的动态规划算法,利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图——篱笆网络的有向图(Lattice )的最短路径问题而提出的。 凡是使用隐含马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。——摘自《数学之美》
给定某一个观察者序列Y= {y1, y2, ..., yn}, 而产生它们的隐含状态为X={x1, x2, ..., xn}, 其中在任意时刻t(即观察者)下,其对应的隐含状态存在多种可能;若将每个观察者视为一步,则每步是一个多选择问题。如图-1所示为维特比算法的数学表达式, 其目标即为获取最大概率值下的隐含状态序列:
![]()
图-1 维比特算法数学表达式
此外,若将上述隐含状态序列按值进行展开,则会得到常见的篱笆网络结构,如图-2所示:
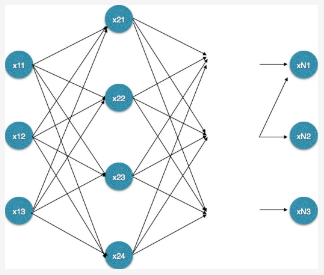
图-2 篱笆网络
维特比算法利用动态规划思想求解概率最大路径(可理解为求图最短路径问题), 其时间复杂度为O(N*L*L),其中N为观察者序列长度,L为隐含状态大小。该算法的核心思想是:通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况,即在每一步的所有选择都保存了前继所有步骤到当前步骤当前选择的最小总代价(或者最大价值)以及当前代价的情况下后续步骤的选择。依次计算完所有步骤后,通过回溯的方法找到最优选择路径。
简单来说,在计算第t+1时刻的最短路径时,只需要考虑从开始到当前t时刻下k个状态值的最短路径和当前状态值到第t+1状态值的最短路径即可。如求t=3时的最短路径,等于求t=2时的所有状态结点x2t(见上图-2所示)的最短路径再加上t=2到t=3的各节点的最短路径。
以下将从源代码的角度,对维比特算法进行剖析,分别从wikipedia、HanLP以及个人冗余代码3种实现方式进行剖析。
源码之Wiki(有改动)
public class Viterbi { private static class TNode { public int[] v_path; // 节点路径 public double v_prob; // 概率累计值 public TNode( int[] v_path, double v_prob) { this.v_path = copyIntArray(v_path); this.v_prob = v_prob; } } private static int[] copyIntArray(int[] ia) { // 数组拷贝 int[] newIa = new int[ia.length]; System.arraycopy(ia, 0, newIa, 0, ia.length); // 较wiki源码有改动 return newIa; } private static int[] copyIntArray(int[] ia, int newInt) { // 数组拷贝 int[] newIa = new int[ia.length + 1]; System.arraycopy(ia, 0, newIa, 0, ia.length); // 较wiki的源码稍有改动 newIa[ia.length] = newInt; return newIa; } // forwardViterbi(observations, states, start_probability, // transition_probability, emission_probability) public int[] forwardViterbi(String[] y, String[] X, double[] sp, double[][] tp, double[][] ep) { TNode[] T = new TNode[X.length]; for (int state = 0; state < X.length; state++) { int[] intArray = new int[1]; intArray[0] = state; T[state] = new TNode(intArray, sp[state] * ep[state][0]); } for (int output = 1; output < y.length; output++) { TNode[] U = new TNode[X.length]; for (int next_state = 0; next_state < X.length; next_state++) { int[] argmax = new int[0]; double valmax = 0; for (int state = 0; state < X.length; state++) { int[] v_path = copyIntArray(T[state].v_path); double v_prob = T[state].v_prob; double p = ep[next_state][output] * tp[state][next_state]; v_prob *= p; // 核心元语 if (v_prob > valmax) { // 每一轮会增加节点 if (v_path.length == y.length) { // 最终截止 argmax = copyIntArray(v_path); } else { argmax = copyIntArray(v_path, next_state); // 增加新的节点 } valmax = v_prob; } } // the number 3 for U[next_state] = new TNode(argmax, valmax); } // the number 2 for T = U; } // apply sum/max to the final states: int[] argmax = new int[0]; double valmax = 0; for (int state = 0; state < X.length; state++) { int[] v_path = copyIntArray(T[state].v_path); double v_prob = T[state].v_prob; if (v_prob > valmax) { argmax = copyIntArray(v_path); valmax = v_prob; } } return argmax; } }
该算法的核心在于,内部类TNode中维护了一个动态数组v_path, 它随着每一轮的迭代,即观察者序列按序迭代时,其路径长度在动态递增;同时伴随着概率累积值v_prob在更新。由于v_path中是按照正序维护了观察者序列按序到达最终节点中的局部概率最大值所对应的隐含状态序列,因此该算法不需要进行回溯求解路径。
源码之HanLP
public class Viterbi { /** * 求解HMM模型 * @param obs 观测序列 * @param states 隐状态 * @param start_p 初始概率(隐状态) * @param trans_p 转移概率(隐状态) * @param emit_p 发射概率 (隐状态表现为显状态的概率) * @return 最可能的序列 */ public static int[] compute(int[] obs, int[] states, double[] start_p, double[][] trans_p, double[][] emit_p) { double[][] V = new double[obs.length][states.length]; int[][] path = new int[states.length][obs.length]; for (int y : states) { V[0][y] = start_p[y] * emit_p[y][obs[0]]; path[y][0] = y; } for (int t = 1; t < obs.length; ++t) { int[][] newpath = new int[states.length][obs.length]; for (int y : states) { double prob = -1; int state; for (int y0 : states) { double nprob = V[t - 1][y0] * trans_p[y0][y]
* emit_p[y][obs[t]]; // 核心元语 if (nprob > prob) { prob = nprob; state = y0; V[t][y] = prob; // 记录最大概率 System.arraycopy(path[state], 0, newpath[y], 0, t); // 记录路径 newpath[y][t] = y; } } } path = newpath; } double prob = -1; int state = 0; for (int y : states) { if (V[obs.length - 1][y] > prob) { prob = V[obs.length - 1][y]; state = y; } } return path[state]; } }
从上述代码可知,HanLP与Wiki中的实现比较类似,按照正序维护了最大概率所对应的路径,因此也无需进行回溯。
源码之冗余代码
public static List<Integer> Viterbi(int[] obState, String[] termList, double[] hiddenState, double[][]transitionMatrix, double[][]emitterMatrix) { int len = obState.length; int labelSize = hiddenState.length; double[][] result = new double[len][labelSize]; int[][] max = new int[len][labelSize]; double tmp = 0; // 初始化 for (int i = 0; i < labelSize; i++) { result[0][i] = hiddenState[i] * emitterMatrix[i][obState[0]]; // 对初始行进行赋值 } // 迭代 for (int i = 1; i < len; i++) { for (int j = 0; j < labelSize; j++) { tmp = result[i-1][0] * transitionMatrix[0][j] * emitterMatrix[j][obState[i]]; max[i][j] = 0; for (int k = 1; k < labelSize; k++) { // 初始值时从0开始,则此处从1开始 double prob = result[i-1][k] * transitionMatrix[k][j]
* emitterMatrix[j][obState[i]]; // 核心元语 if (prob > tmp) { tmp = prob; max[i][j] = k; // 保存路径节点 } result[i][j] = tmp; } } } // 从结束点开始 List<Integer> adjList = new ArrayList<Integer>(); int maxNode = 0; double maxValue = result[len-1][0]; for (int k = 1; k < labelSize; k++) { // maxValue 默认从0开始, 则此处从1开始 if (result[len-1][k] > maxValue) { maxValue = result[len-1][k]; maxNode = k; } } adjList.add(maxNode); // 回溯 for (int i = len-1; i > 0; i--) { maxNode = max[i][maxNode]; adjList.add(maxNode); } // 获取结果 List<Integer> retList = new ArrayList<Integer>(); for (int i = adjList.size()-1; i >= 0; i--) { retList.add(adjList.get(i)); } return retList; }
该部分冗余代码为个人所写,从代码流程来看,它从初始化到回溯整个过程都进行详细的阐述。尤其需要注意注释中“默认从0开始, 则此处从1开始”的部分,其中更多的从代码简化的角度进行了一定的优化工作。
总结
上述3种实现,均可以在实际工程中应用,个人强烈推荐采用第1和第2,第3种作为学习可以参考。维特比算法只是解决隐马尔科夫第三个问题(求观察序列的最可能的标注序列)的一种实现方式,因此维特比算法和隐马尔科夫模型不能等价。涉及多步骤每步多选择模型的最优选择问题,可采用该算法来解决。
参考内容:
1) 吴军. 数学之美.
2) HanLP-Viterbi: https://github.com/hankcs/Viterbi/blob/master/src/com/hankcs/algorithm/Viterbi.java
3) Wikipedia-Viterbi:https://en.wikibooks.org/wiki/Algorithm_Implementation/Viterbi_algorithm
4) http://www.cnblogs.com/ryuham/p/4686496.html
作者:志青云集
出处:http://www.cnblogs.com/lyssym
如果,您认为阅读这篇博客让您有些收获,不妨点击一下右下角的【推荐】。
如果,您希望更容易地发现我的新博客,不妨点击一下左下角的【关注我】。
如果,您对我的博客所讲述的内容有兴趣,请继续关注我的后续博客,我是【志青云集】。
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则将依法追究法律责任。