描述
小C同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一棵包含n个结点和n - 1条边的树,每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到n的连续正整数。
现在有m个玩家,第i个玩家的起点为Si,终点为Ti。每天打卡任务开始时,所有玩家 在第0秒 同时从 自己的起点 出发,以 每秒跑一条边 的速度,不间断地沿着最短路径向着 自己的终点 跑去,跑到终点后该玩家就算完成了打卡任务。(由于地图是一棵树,所以每个人的路径是唯一的)
小C想知道游戏的活跃度,所以在每个结点上都放置了一个观察员。在结点j的观察员会选择在第Wj秒观察玩家,一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也 正好 到达了结点j。小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏,他不能等待一段时间后再被观察员观察到。即对于把结点j作为终点的玩家:若他在第Wj秒前到达 终点,则在结点j的观察员 不能观察到 该玩家;若他 正好 在第Wj秒到达终点,则在结点j的观察员 可以观察到 这个玩家。
格式
输入格式
第一行有两个整数n和m。其中n代表树的结点数量,同时也是观察员的数量, m代表玩家的数量。
接下来n - 1行每行两个整数u和v,表示结点u到结点v有一条边。
接下来一行n个整数,其中第j个整数为Wj,表示结点j出现观察员的时间。 接下来m行,每行两个整数Si和Ti,表示一个玩家的起点和终点。
对于所有的数据,保证1 <= Si, Ti <= n,0 <= Wj <= n。
输出格式
输出1行n个整数,第j个整数表示结点j的观察员可以观察到多少人。
样例1
样例输入1
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
样例输出1
2 0 0 1 1 1
样例2
样例输入2
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
样例输出2
1 2 1 0 1
限制
每个测试点时限2秒。
【子任务】
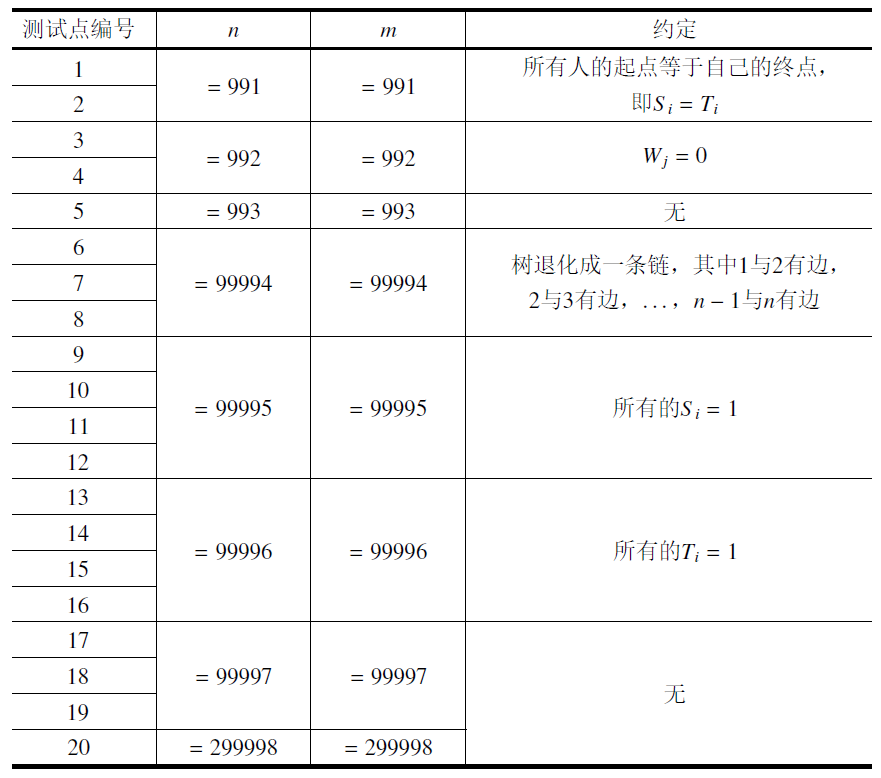
每个测试点的数据规模及特点如下表所示。提示:数据范围的个位上的数字可以帮助判断是哪一种数据类型。
提示
【样例1说明】
对于1号点,W1=0,故只有起点为1号点的玩家才会被观察到,所以玩家1和玩家2被观察到,共2人被观察到。
对于2号点,没有玩家在第2秒时在此结点,共0人被观察到。
对于3号点,没有玩家在第5秒时在此结点,共0人被观察到。
对于4号点,玩家1被观察到,共1人被观察到。
对于5号点,玩家2被观察到,共1人被观察到。
对于6号点,玩家3被观察到,共1人被观察到。
来源
NOIP 2016 提高组 Day 1 第二题
—————————————————————————
这道题我写的 O(n)的扫描线 但是预处理要 nlogn QAQ
其实可以写成 O(n)但是有点复杂就没写
我们把修改(就是走来走去的玩家)拆成四个修改
就是类似差分的方法
一个修改从 从u开始到v结束
我们就拆成四份 在u处+ v处+ (u和v的)lca处- lca的父亲处-
这样就实现了在u和v的路径上加的操作 画个图感受一下吧

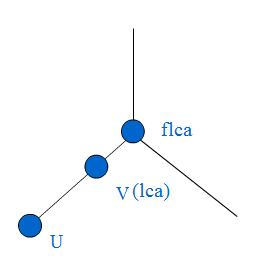
其余类似辣 一共四种情况自己画一下就好了
然后我们考虑一个修改对某个点答案的影响 分两类
第一类是从下往上经过一个点的
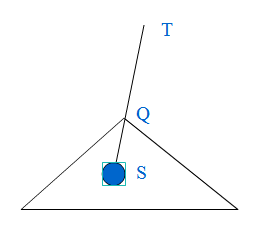
观察可知 S+dis【s】【q】(s q的距离)==w【q】(观察的时间)
满足上一条件那么ans【q】就会被影响
当然因为做扫描线我们需要把形式转换为只和询问和修改有关
又 dis【s】【q】=d【s】-d【q】(d表示深度)
即S+d【s】=w【q】+d【q】
第二类为从上往下经过一个点的情况
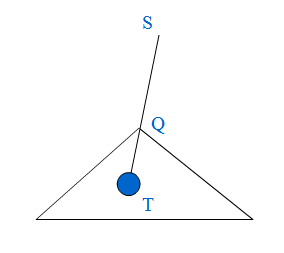
同理 满足的条件为 T-d【T】【q】==w【q】
转换为 T-d【T】=w【q】-d【q】
当然因为形式不同 所以要分开存 最后合起来就好了(开两个桶)
这样之后我们就找到了询问和修改的关系了
然后我们发现对一个点有影响的修改当且仅当修改在他的子树内
这样我们可以做一次dfs dfs到一个点的时候记录一波ans1
回溯到一个点说明关于他的修改已经全部加上了
这个时候再记录一波ans2 那么这个点的答案就是ans2-ans1
这样就实现了询问的拆分了 这样这个问题就解决了 代码其实很短
但是细节较多

#include<cstdio> #include<cstring> #include<algorithm> #include<vector> const int M=5e5+7; int read(){ int ans=0,f=1,c=getchar(); while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();} while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();} return ans*f; } int n,m; int first[M],cnt; struct node{int to,next;}e[2*M]; void ins(int a,int b){e[++cnt]=(node){b,first[a]}; first[a]=cnt;} void insert(int a,int b){ins(a,b); ins(b,a);} int w[M]; int dep[M],f[M][25]; void dfs(int x){ for(int i=1;(1<<i)<=dep[x];i++) f[x][i]=f[f[x][i-1]][i-1]; for(int i=first[x];i;i=e[i].next){ int now=e[i].to; if(!dep[now]){ dep[now]=dep[x]+1; f[now][0]=x; dfs(now); } } } int find(int x,int y){ if(dep[x]<dep[y]) std::swap(x,y); int d=dep[x]-dep[y]; for(int i=0;(1<<i)<=d;i++) if(1<<i&d) x=f[x][i]; if(x==y) return x; for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } struct pos{int x,s;}; std::vector<pos>e1[M],e2[M]; int ans1[2*M],ans2[2*M],ans[M]; void pans(int x){ ans[x]-=ans1[w[x]+dep[x]]; ans[x]-=ans2[w[x]-dep[x]+n]; pos*p=e1[x].data(); for(int i=0;i<e1[x].size();i++) ans1[p[i].x]+=p[i].s; p=e2[x].data(); for(int i=0;i<e2[x].size();i++) ans2[p[i].x+n]+=p[i].s; for(int i=first[x];i;i=e[i].next){ int now=e[i].to; if(f[x][0]==now) continue; pans(now); } ans[x]+=ans1[w[x]+dep[x]]; ans[x]+=ans2[w[x]-dep[x]+n]; } int main(){ int x,y; n=read(); m=read(); for(int i=1;i<n;i++) x=read(),y=read(),insert(x,y); for(int i=1;i<=n;i++) w[i]=read(); dep[1]=1; dfs(1); for(int i=1;i<=m;i++){ x=read(); y=read(); int lca=find(x,y),fa=f[lca][0]; e1[x].push_back((pos){dep[x],1}); e1[lca].push_back((pos){dep[x],-1}); e2[y].push_back((pos){dep[x]-2*dep[lca],1}); e2[fa].push_back((pos){dep[x]-2*dep[lca],-1}); } pans(1); for(int i=1;i<=n;i++) printf("%d ",ans[i]); printf(" "); return 0; }