You are given a boolean function of three variables which is defined by its truth table. You need to find an expression of minimum length that equals to this function. The expression may consist of:
- Operation AND ('&', ASCII code 38)
- Operation OR ('|', ASCII code 124)
- Operation NOT ('!', ASCII code 33)
- Variables x, y and z (ASCII codes 120-122)
- Parentheses ('(', ASCII code 40, and ')', ASCII code 41)
If more than one expression of minimum length exists, you should find the lexicographically smallest one.
Operations have standard priority. NOT has the highest priority, then AND goes, and OR has the lowest priority. The expression should satisfy the following grammar:
E ::= E '|' T | T
T ::= T '&' F | F
F ::= '!' F | '(' E ')' | 'x' | 'y' | 'z'
The first line contains one integer n — the number of functions in the input (1 ≤ n ≤ 10 000).
The following n lines contain descriptions of functions, the i-th of them contains a string of length 8 that consists of digits 0 and 1 — the truth table of the i-th function. The digit on position j (0 ≤ j < 8) equals to the value of the function in case of  ,
, 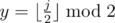 and
and  .
.
You should output n lines, the i-th line should contain the expression of minimum length which equals to the i-th function. If there is more than one such expression, output the lexicographically smallest of them. Expressions should satisfy the given grammar and shouldn't contain white spaces.
4
00110011
00000111
11110000
00011111
y
(y|z)&x
!x
x|y&z
The truth table for the second function:
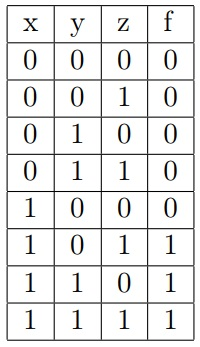
大意:给出三个八位二进制数x,y,z,允许使用!、&、| 运算,也可以加括号。
给出N个数(都是八位二进制数),求用x、y、z组成的最短的表达式中字典序最小的。
题解:考场上我肯定做不出来的,这题又是一个很奇怪的dp
由于表达式间有明确的优劣关系,可以直接用表达式字符串作为状态。
E[i]表示最后进行的运算是 | 的值为 i 的表达式
T[i]表示最后进行的运算是 & 的值为 i 的表达式
F[i]表示最后进行的运算是 ! 的值为 i 的表达式
最后进行的是括号运算的表达式性质与F相似,归为一类。
起始状态("x","y","z")表达式性质与F相似,归为一类。
那么状态转移怎么做?
先上图

1、2是题目中提到的转移方式,5应该不用解释
关键在于3、4,思考:F[i]的性质一定满足T[i]的性质,T[i]的性质一定满足E[i]的性质。(这需要联系运算符优先级思考)
所以把F[i]当做T[i],T[i]当做E[i]来用稳赚不亏
这样,!操作只需要对F做就行了,因为F可以向T和E传递。
需要注意的是转移顺序:
1一定在2之前。
3一定在4之前。
不然~~~~~~~时间复杂度常数会大一点(其实也没事)。
这样五种转移为一轮,当整整一轮没有做有效更新时结束就行了。
/*
Welcome Hacking
Wish You High Rating
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
using namespace std;
int read(){
int xx=0,ff=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){xx=(xx<<3)+(xx<<1)+ch-'0';ch=getchar();}
return xx*ff;
}
const int X=15,Y=51,Z=85;
string E[256],T[256],F[256];//E:| T:& F:!
bool flag;
void upd(string &A,const string&B){
if(A==""){
A=B;
flag=1;
return;
}
int t1=A.size(),t2=B.size();
if(t1>t2)
A=B,flag=1;
else if(t1==t2)
if(A>B)
A=B,flag=1;
}
int main(){
//freopen("in","r",stdin);
//freopen("out","w",stdout);
F[X]='x',F[Y]='y',F[Z]='z';
while(1){
flag=0;
for(int i=0;i<=255;i++)
if(T[i]!="")
for(int j=0;j<=255;j++)
if(F[j]!="")
upd(T[i&j],T[i]+'&'+F[j]);
for(int i=0;i<=255;i++)
if(E[i]!="")
for(int j=0;j<=255;j++)
if(T[j]!="")
upd(E[i|j],E[i]+'|'+T[j]);
for(int i=0;i<=255;i++)
if(E[i]!="")
upd(F[i],'('+E[i]+')');
for(int i=0;i<=255;i++)
if(F[i]!="")
upd(T[i],F[i]);
for(int i=0;i<=255;i++)
if(T[i]!="")
upd(E[i],T[i]);
for(int i=0;i<=255;i++)
if(F[i]!="")
upd(F[i^255],'!'+F[i]);
if(!flag)
break;
}
int T,N;
char s[10];
T=read();
while(T--){
gets(s);
N=0;
for(int i=0;i<=7;i++)
N=(N<<1)+s[i]-'0';
cout<<E[N]<<endl;
}
return 0;
}
最短路+记录路径应该也可做,但是~~~应该很麻烦。