二分查找总结

最近刷leetcode，做了挺多道二分查找的题目，感觉二分查找并没有想象中的简单，一些变形题还是有一定难度的，所以这里做一个总结，方便自己以后复习。

首先，二分查找一般有两种写法

左闭右闭写法

int search(vector<int> &nums, int target){
    int left = 0, right = nums.size() - 1, mid; //注意，right的初始值是nums.size()-1，而不是nums.size()
    while (left <= right){ //注意，是≤，不是＜
        mid = left + ((right - left) >> 1); //注意，写成 mid = (left+right)/2 有可能发生溢出，除法换成移位操作可以提升计算速度，移位运算记得加括号，因为优先级比加号低
        if (nums[mid] == target){ //找到了
            return mid;
        }
        else if (nums[mid] < target){ //更新左边界
            left = mid + 1;
        }
        else{ //更新右边界
            right = mid - 1;
        }
    }

    return -1; //注意，如果执行到这里来了，说明没有找到目标元素，返回-1，因为如果找得到目标元素，则一定会进入循环里面的 if(nums[mid] == target)
}

左闭右开写法

int search(vector<int> &nums, int target){
    int left = 0, right = nums.size(), mid; //注意，right的初始值是nums.size()，而不是nums.size()-1
    while (left < right){ //注意，是＜，不是≤
        mid = left + ((right - left) >> 1); //同上
        if (nums[mid] == target){ //找到了
            return mid;
        }
        else if (nums[mid] < target){ //更新左边界
            left = mid + 1;
        }
        else{ //更新右边界，注意，这种情况下不是 mid-1
            right = mid;
        }
    }

    return -1;
}

以上两种写法在大部分情况下是等价的，不过有些题目却只能用其中一种写法来书写，这个还是得依据具体的题目去分析。

但是，从以上两种写法，我们发现，在二分查找题目中，有这几点是需要我们注意的：

• right的初始值，是选择 nums.size()，还是选择 nums.size()-1
• 循环条件，是 left < right，还是 left <= right
• right如何更新，是 right = mid，还是 right = mid - 1
• 可能还有一点，就是有些时候循环最后还要返回一个值，是返回 left，还是返回 mid

所以，其实你去仔细思考的话，二分查找还是不那么容易想明白的。

下面我就记录一下几道自己在leetcode上做到的二分查找题，个人感觉有一定的代表性。

目录

• 34. Find First and Last Position of Element in Sorted Array
• 33. Search in Rotated Sorted Array
• 81. Search in Rotated Sorted Array II
• 153. Find Minimum in Rotated Sorted Array
• 154. Find Minimum in Rotated Sorted Array II

34. Find First and Last Position of Element in Sorted Array

这道题我在 网上 看到这么一种写法：
先找第一个大于等于target的数，记这个位置为low；然后再找第一个大于等于target+1的数，记这个位置为high。那么target的范围就是{low, high-1}。
于是我们先得写一个子函数，就是找到第一个大于等于target的数的位置

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int start = firstGreaterEqual(nums, target);
        if (start == nums.size() || nums[start] != target) return {-1, -1};
        return {start, firstGreaterEqual(nums, target + 1) - 1};
    }

    int firstGreaterEqual(vector<int>& nums, int target) {
        int left = 0, right = nums.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        return right;
    }
};

个人觉得不是很好想出来，而且你会发现，firstGreaterEqual这个函数一些变量的更新和之前标准的二分查找有点不一样了。

于是我写了一个更好理解的代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int start_idx = find(nums, target, 0);
        if(start_idx == -1) return {-1, -1};
        else return {start_idx, find(nums, target, 1)};
    }
    
    int find(vector<int>& nums, int target, int tag){
        int left = 0, right = nums.size()-1, mid;
        while(left <= right){
            mid = (left + right)/2;
            if(target == nums[mid]){
                if(tag == 0){//表示找最左边的
                    if(mid > 0 && nums[mid-1] == target) right = mid-1;
                    else return mid;
                }
                else{//表示找最右边的
                    if(mid < nums.size()-1 && nums[mid+1] == target) left = mid + 1;
                    else return mid;
                }
            }
            else if(target < nums[mid]) right = mid-1;
            else left = mid + 1;
        }

        return -1;
    }
};

其他部分跟标准的二分查找一样，就是当我们找到target的时候，不能停下来，我们需要判断是否需要接着往左边找或者往右边找，
当我们需要查找最左边的哪个target时，我们需要判断当前这个target是否已经是最左边的了，如果不是，那么接着往左边找，同理，找最右边的也是这个逻辑。

33. Search in Rotated Sorted Array

读过题目之后，我们发现，Rotated Sorted Array 其实是长下面这个样子的：

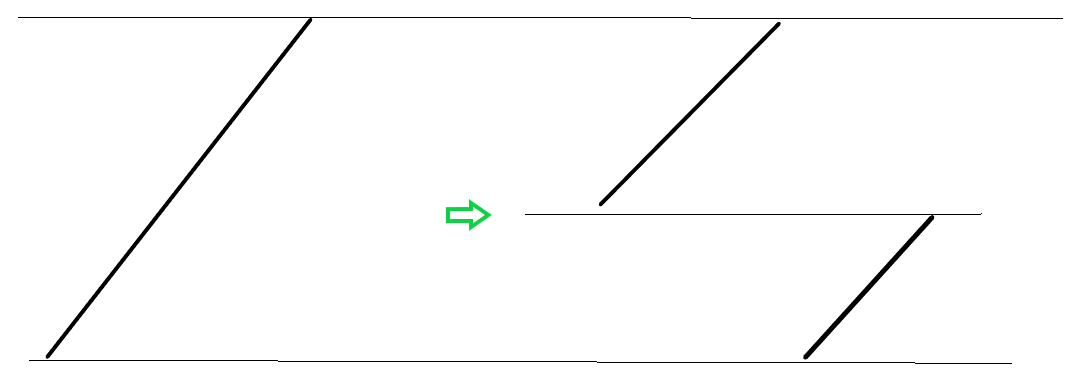
这个图的意思就是数组右半段跑到左边去了，需要注意的是，这个数组是不包含重复数字的，所以 旋转过后左半段的最左边数字 一定大于 右半段的最右边的数字

所以接下来我们的代码这么写

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = (left + right)/ 2;
            if (nums[mid] == target) return mid;
            if (nums[mid] <= nums[right]) {
                if (target > nums[mid] && target <= nums[right]) left = mid + 1;
                else right = mid - 1;
            }
            else {
                if (target >= nums[left] && target < nums[mid]) right = mid - 1;
                else left = mid + 1;
            }
        }

        return -1;
    }
};

注意，当我们发现 target != nums[mid]的时候，接下来该怎么办呢？这个地方估计是很多人卡到的地方，
主要问题就是我们不知道现在mid是处于左边半段还是右边半段，那么如何确定我们所在的位置呢？就是通过和nums[right]比较，如果小于或者等于nums[right]，说明mid在右半段，否则在左半段。

现在问题又变成了，我们知道了mid在左边还是右边，接下来如何更新left或者right的值呢？

其实我们发现，无论是到了左半段还是右半段，我们都存在一个接下来往左还是往右继续搜索的问题。所以里面还有一个ifelse判断。

81. Search in Rotated Sorted Array II

这个题和上一个题唯一的区别就是 数组中允许出现重复数字，别小看这一个区别，这可能给我们接下来的搜索带来不小的问题。

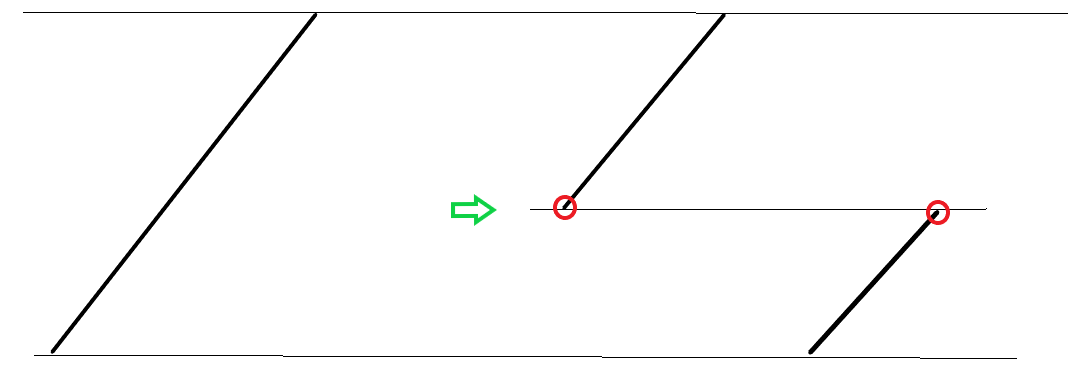
现在数组变成了下面这个样子

就是一开始的时候，nums[left]的值是有可能等于nums[right]的，当然，中间也可能出现这种情况

那么这怎么解决呢，既然nums[left]可能等于nums[right]，那么我们就从nums[left]下手。

先看一下完整代码:

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int left = 0, right = nums.size()-1, mid;
        while(left <= right){
            mid = (left+right)/2;
            if(target == nums[mid]) return true;
            if(nums[left] == nums[mid]){
                //无法判断[left...mid]和[mid...right]两个区间哪个是有序的
                left++;
            }
            else if(nums[mid] <= nums[right]){//[mid...right]区间是递增的
                if(target > nums[mid] && target <= nums[right]) left = mid+1;
                else right = mid-1;
            }
            else{//[left...mid]区间是递增的
                if(target >= nums[left] && target < nums[mid]) right = mid-1;
                else left = mid+1;
            }
        }
        
        return false;
    }
};

首先，如果target==nums[mid]的时候我们自然返回true就行，这跟最原始的二分查找是一样的。

然后，我们发现target != nums[mid]的时候，就去比较nums[mid]和nums[left]的值，注意，nums[left]是可能等于nums[right]的。

• 如果nums[left] == nums[mid]，那么我们并不知道mid是在左半段，还是在右半段，也就无法判断[left...mid]和[mid...right]两个区间哪个是有序的，这种情况下，我们就让left++，因为target此时是不等于nums[left]的，自然可以跳过它

• 如果nums[mid] <= nums[right]，那么分两种情况

  • 一种是刚好等于nums[right]，说明这时候nums[left]是不等于nums[left]的，否则就会进上一个判断条件，这说明，mid此时就是在右半段
  • 还有一种就是nums[mid] < nums[right]，这时候自然也说明mid是在右半段的，因为左半段的数字都大于等于nums[right]
    于是这时候就回到了上一题的判断逻辑，就是在右半段去看一下接下来往左查询还是往右查询

• 如果nums[mid] > nums[right]，那么自然是去左半段找了，接下来的过程还是分为往左还是往右继续搜索
  
  
  

注意下面这两道题，同样是基于 Rotated Sorted Array 结构上的查找，虽然可以用二分查找做，但是用分治法明显更简单

153. Find Minimum in Rotated Sorted Array

这道题规定了数组的元素不重复
代码如下：

class Solution {
public:
    int findMin(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1);
    }
    
    int helper(vector<int>& nums, int start, int end){
        if(nums[start] <= nums[end]) return nums[start];
        int mid = start + ((end-start)>>1);
        return min(helper(nums, start, mid), helper(nums, mid+1, end));
    }
};

你会发现这个函数及其简单，试想，加入我们数组没被翻转过，那么你如何快速查找数组的最小值？

那很简单啊，就是第一个值呀，因为数组已经是按照升序排列的。
那怎么判断一个序列是不是没有翻转过呢？或者说，怎么知道数组的某一个部分是升序的？
很简单，假设这个子片段开始下标是start，结束下标是end，那么加入nums[start] < nums[end]，说明这个子序列是有序的，其中最小值就是nums[start]。

但是，我们在递归过程中，可能出现 start等于end 的情况，只包含一个元素的序列也是有序的，
所以当nums[start] <= nums[end]时，说明这个子序列[start...end]是有序的，直接返回其中的最小值nums[start]
当然这有一个前提，就是数组中不包含重复的数字，如果包含，当nums[start]==nums[end]的时候，[start...end]是不一定有序的。例如[3,1,3]

如果这段子序列无序，则说明最小值可能存在于[left...mid]，也可能存在于[mid+1...end]，于是我们递归计算两边的最小值，去两者中更小的值作为本次调用的最小值。
注意，有些人递归调用可能写成下面这个样子：
min(helper(nums, start, mid-1), helper(nums, mid, end));
这样是会出现错误的，可以自己去试试。

154. Find Minimum in Rotated Sorted Array II

这道题允许数组的元素重复

这道题和上一道题的唯一区别就在于，当我们发现 nums[start]==nums[end] 的时候，不能直接判断[start...end]之间是否是有序的，也就无法判断其中的最小值是nums[start]。
例如出现[3,1,3]的时候，最小值并不是3，而是1

那么怎么办呢？很好办，只需要在这里改造一下上一道题的代码。

class Solution {
public:
    int findMin(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    int helper(vector<int>& nums, int start, int end) {
        if (start == end) return nums[start];
        else {
            if (nums[start] < nums[end]) return nums[start];
            else {
                int mid = start + ((end - start) >> 1);
                return min(helper(nums, start, mid), helper(nums, mid+1, end));
            }
        }
    }
};

当我们nums[start] < nums[end]的时候，这一段是肯定有序的，其他情况我们都拆成两段递归。