「算法笔记」可持久化线段树

一、引入

有的时候，我们不仅需要支持修改，还需要支持访问历史版本。

这个时候普通的线段树就没法胜任了，因为每次我们都覆盖了之前的版本。

若想知道数据集在任意时间的历史状态，有没有什么方法呢？

方法一：直接记录之前得到的所有的线段树。在第 i 项操作结束后（∀i∈[1,M]），把整个线段树拷贝一遍，存储在 history[i] 中，多耗费 M 倍的空间。

复杂度 O(n²)。

方法二：注意到每次修改的位置都不会很多，所以相同的节点就没必要再记录一遍了。

复杂度 O(n log n)。

比如说要对 15 号节点进行“单点修改”，我们需要新建节点，如下图所示，白色的为最初版本的线段树，红色的为版本 2。产生了 O(logN) 个新节点。

唯一的问题是由于需要每次新建节点，我们没办法再用位运算（p<<1,p<<1|1）访问子节点，而需要在每一个点上记录左右儿子的位置。

这就是可持久化线段树（主席树）的基本思想。

二、区间第 k 小

Luogu P3834 主席树模板题

题目大意：长度为 n 的数组，每次查询一段区间里第 k 小的数。1≤n,q≤2×10⁵。

Solution：

我们先考虑一个比较简单的问题：如何维护全局第 k 小？

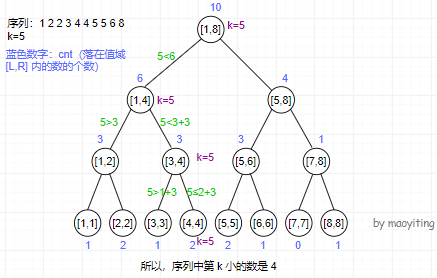
维护序列中落在值域区间 [L,R] 中数的个数（记作 cnt_L,R）。比较 cnt_L,mid 与 k 的大小关系，即可确定序列中第 k 小的数是 ≤mid 还是 >mid，从而可以进入线段树的左、右子树之一。换言之，可以建一棵权值线段树，然后在线段树上二分解决。 

维护前缀第 k 大？

把这个权值线段树可持久化，这样我们就可以随时拎出来一个前缀。

区间第 k 大？

相当于两个线段树相减（类似前缀和？），同样可以用可持久化线段树维护。

“root[r] 的值域区间 [L,R] 的 cnt 值”-“root[l-1] 的值域区间 [L,R] 的 cnt 值”=“序列中落在值域 [L,R] 内的数的个数”，也就是可持久化线段树中两个代表相同值域的节点具有可减性。

时间复杂度 O(n log n)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n,m,l,r,k,tot,a[N],t,b[N],lc[N<<5],rc[N<<5],sum[N<<5],root[N];    //lc[],rc[]:左右子节点编号  tot:可持久化线段树的总点数  root[]:可持久化线段树的每个根 
void build(int &p,int l,int r){    //建出一棵初始时的的树
    p=++tot,sum[p]=0;    //新建一个节点
    if(l==r) return ;
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int insert(int p,int l,int r,int pos,int ave){
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p],sum[x]=sum[p];    //动态开点，先复制原来的节点 
    if(l==r){sum[x]+=ave;return x;}
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=insert(lc[p],l,mid,pos,ave);
    else rc[x]=insert(rc[p],mid+1,r,pos,ave);
    sum[x]=sum[lc[x]]+sum[rc[x]];
    return x; 
} 
int query(int x,int y,int l,int r,int k){    //在 x,y 两个节点上，值域为 [l,r]，求第 k 小的数 
    if(l==r) return l;    //找到答案 
    int mid=(l+r)/2,v=sum[lc[x]]-sum[lc[y]],ans=0;    //v:有多少个数落在值 [l,mid] 内 
    if(v>=k) ans=query(lc[x],lc[y],l,mid,k);
    else ans=query(rc[x],rc[y],mid+1,r,k-v);
    return ans;
} 
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]),b[++t]=a[i];
    sort(b+1,b+1+t),t=unique(b+1,b+1+t)-b-1;    //离散化 
    build(root[0],1,t); 
    for(int i=1;i<=n;i++){
        int x=lower_bound(b+1,b+1+t,a[i])-b;
        root[i]=insert(root[i-1],1,t,x,1);    //在上一个版本的基础上修改
    }
    while(m--){
        scanf("%lld%lld%lld",&l,&r,&k);
        int x=query(root[r],root[l-1],1,t,k); 
        printf("%lld
",b[x]);
    }
    return 0;
}

三、树上第 k 小

Luogu P2633 Count on a tree

题目大意：n 个点的一棵树，每次查询一条链 u,v 上第 k 小的数。1≤n,q≤10⁵。

Solution：

树链剖分，然后可持久化，每次拿出来 O(log n) 个线段树进行二分，……

恭喜你想到了一个 O(n log³ n) 的算法。

我们注意到，在可持久化线段树上，我们的 root[x] 不一定去依赖 root[x-1]，完全可以依赖别的位置。

所以我们可以每一个点依赖它的父节点。这样每一个点的线段树就是维护的它到根节点的信息。

对于一条链 u...v，我们设 u 和 v 的 LCA 是 d，那么只需要在 T(u)+T(v)-T(d)-T(fa(d)) 上进行二分即可。

时间复杂度 O(n log n)。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
int n,m,x,y,k,lastans,tot,a[N],t,b[N],lc[N<<5],rc[N<<5],sum[N<<5],root[N],cnt,hd[N],to[N<<1],nxt[N<<1],dep[N],f[N][30];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void build(int &p,int l,int r){
    p=++tot,sum[p]=0;
    if(l==r) return ;
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int insert(int p,int l,int r,int pos,int ave){
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p],sum[x]=sum[p];
    if(l==r){sum[x]+=ave;return x;}
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=insert(lc[p],l,mid,pos,ave);
    else rc[x]=insert(rc[p],mid+1,r,pos,ave);
    sum[x]=sum[lc[x]]+sum[rc[x]];
    return x; 
} 
int query(int a,int b,int c,int d,int l,int r,int k){
    if(l==r) return l;
    int mid=(l+r)/2,v=sum[lc[a]]+sum[lc[b]]-sum[lc[c]]-sum[lc[d]],ans=0;    //T(u)+T(v)-T(d)-T(fa(d))
    if(v>=k) ans=query(lc[a],lc[b],lc[c],lc[d],l,mid,k);
    else ans=query(rc[a],rc[b],rc[c],rc[d],mid+1,r,k-v);
    return ans;
} 
void dfs(int x,int fa){    //预处理 
    root[x]=insert(root[fa],1,t,lower_bound(b+1,b+1+t,a[x])-b,1);    //每一个点依赖它的父节点
    dep[x]=dep[fa]+1;
    for(int i=0;i<=19;i++)
        f[x][i+1]=f[f[x][i]][i];
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y!=fa) f[y][0]=x,dfs(y,x);
    }
}
int LCA(int x,int y){    //求 LCA 
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=20;i>=0;i--){
        if(dep[f[x][i]]>=dep[y]) x=f[x][i];
        if(x==y) return x; 
    }
    for(int i=20;i>=0;i--)
        if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]),b[++t]=a[i];
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    sort(b+1,b+1+t),t=unique(b+1,b+1+t)-b-1;    //离散化 
    build(root[0],1,t),dfs(1,0);
    while(m--){
        scanf("%lld%lld%lld",&x,&y,&k),x^=lastans;
        int d=LCA(x,y),v=query(root[x],root[y],root[d],root[f[d][0]],1,t,k);
        printf("%lld
",lastans=b[v]);
    }
    return 0;
}

四、可持久化并查集

并查集的基本操作：

int f[N],sz[N];    //fa、size 
int find(int x){    //查询 
    return x==f[x]?x:f[x]=find(f[x]);    //优化 1:路径压缩 
}
void merge(int x,int y){    //合并 
    x=find(x),y=find(y);
    if(x!=y){
        if(sz[x]<sz[y]) swap(x,y);
        f[y]=x,sz[x]+=sz[y]; 
    }    //优化 2:启发式合并（按秩合并） 
}

首先科普一个关于并查集的知识点：

• 按秩合并 + 路径压缩：O(α(n))（反阿克曼函数）
• 只用按秩合并或只用路径压缩：O(log n)

在某些情况下，我们只能用按秩合并不能用路径压缩，比如可持久化。

然后回归正题。

Luogu P3402 可持久化并查集模板题

题目大意：实现一个可持久化并查集，不光要支持所有并查集的操作，还需要支持访问历史版本。1≤n,q≤10⁵。

Solution：

用可持久化线段树，我们可以实现数组的可持久化。也就是维护一个数组，支持单点修改数组元素和访问历史版本。

并查集，其实无非是维护 fa 和 size，将这两个数组都可持久化，我们就可以实现并查集的可持久化。

不能路径压缩，因为那样的话 fa 会进行很多修改。

时间复杂度 O(n log² n)，两个 log n 一个来自按秩合并并查集一个来自可持久化线段树。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,m,opt,x,y,tot,a[N],lc[N<<5],rc[N<<5],val[N<<5],root[N],sz[N<<5],fa[N<<5];
void build(int &p,int l,int r){
    p=++tot;
    if(l==r){fa[p]=l;return ;}     //初始版本:父亲是它自己
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int modify(int p,int l,int r,int pos,int ave){     //把 pos 的父亲改成 ave 
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p];
    if(l==r){fa[x]=ave,sz[x]=sz[p];return x;}
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=modify(lc[p],l,mid,pos,ave);
    else rc[x]=modify(rc[p],mid+1,r,pos,ave);
    return x; 
} 
int query(int p,int l,int r,int pos){    //询问某一个版本的一个点的父亲
    if(l==r) return p;
    int mid=(l+r)/2,ans=0;
    if(pos<=mid) ans=query(lc[p],l,mid,pos);
    else ans=query(rc[p],mid+1,r,pos);
    return ans;
}  
void add(int p,int l,int r,int pos){
    if(l==r){sz[p]++;return ;}
    int mid=(l+r)/2;
    if(pos<=mid) add(lc[p],l,mid,pos);
    else add(rc[p],mid+1,r,pos); 
}
int find(int p,int v){
    int x=query(p,1,n,v);    //查询在版本 p 中点 v 的父亲 
    return v==fa[x]?x:find(p,fa[x]);    //无路径压缩
}
signed main(){
    scanf("%lld%lld",&n,&m);
    build(root[0],1,n);
    for(int i=1;i<=m;i++){
        scanf("%lld",&opt);
        if(opt==1){
            scanf("%lld%lld",&x,&y);
            root[i]=root[i-1],x=find(root[i],x),y=find(root[i],y);
            if(fa[x]!=fa[y]){
                if(sz[x]<sz[y]) swap(x,y);
                root[i]=modify(root[i-1],1,n,fa[y],fa[x]);    //按秩合并，小的往大的合并
                if(sz[x]==sz[y]) add(root[i],1,n,fa[x]);     //小的增加 size 
            }
        }
        else if(opt==2) scanf("%lld",&x),root[i]=root[x];
        else{
            scanf("%lld%lld",&x,&y);
            root[i]=root[i-1],x=find(root[i],x),y=find(root[i],y);
            if(fa[x]==fa[y]) puts("1");
            else puts("0");
        }
    }
    return 0;
}

另外：若可以不写 build，其实可以不用写，写了反而会变慢。（有一次写了就 T 了，不写就过了 QAQ）