0142. Linked List Cycle II (M)

Linked List Cycle II (M)

题目

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

Example 1:

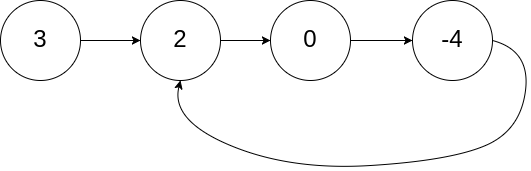
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Follow-up:
Can you solve it without using extra space?

---

题意

判断给定链表中是否存在环,存在则返回环的入口结点。

思路

比较简单的就是将所有遍历到的结点记录下来，如果记录了两次则说明当前结点就是所求的结点。

同样可以使用快慢指针的方法：慢指针每次走一步，快指针每次走两步，如果快指针追上慢指针则说明存在环；当判断出存在环后，将快指针重新指向头结点，步进距离改为一个结点，然后使快指针和慢指针同时继续前进，当两者再次相遇时，所处结点就是所求入口结点。证明如下：

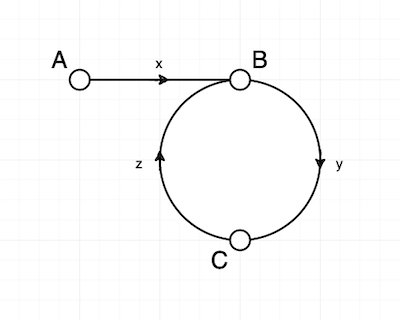
记第一次相遇时慢指针走过的距离为(S_1)，快指针走过的距离为(S_2)，那么可得如下方程组：

[egin{cases} S_1=x+y \ S_2=x+y+n*(y+z) \ S_2=2*S_1 end{cases} ]

化简后可得：

[x=(n-1)*(y+z)+z ]

说明当快指针重新从A点走到B点时，慢指针从C点出发已经走过了n圈加上z的距离，即也正好落在B点上，因此上述方法能够正确找到环的入口结点。

---

代码实现

Java

Hash

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }

        Set<ListNode> set = new HashSet<>();
        while (head != null) {
            if (!set.add(head)) {
                return head;
            }
            head = head.next;
        }

        return null;
    }
}

快慢指针

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }

        ListNode slow = head, fast = head;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                fast = head;
                while (slow != fast) {
                    slow = slow.next;
                    fast = fast.next;
                }
                return slow;
            }
        }

        return null;
    }
}

JavaScript

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function (head) {
  let slow = head
  let fast = head

  while (fast && fast.next) {
    slow = slow.next
    fast = fast.next.next
    if (slow === fast) {
      slow = head
      while (slow !== fast) {
        slow = slow.next
        fast = fast.next
      }
      return slow
    }
  }

  return null
}