0099. Recover Binary Search Tree (H)

Recover Binary Search Tree (H)

题目

You are given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Follow up: A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

Example 1:

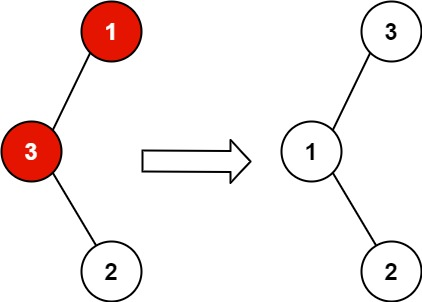
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2:

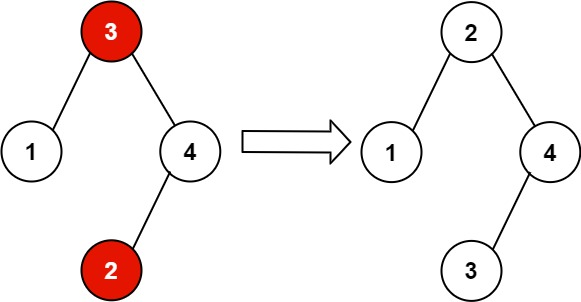
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid. 

Constraints:

• The number of nodes in the tree is in the range [2, 1000].
• -2^31 <= Node.val <= 2^31 - 1

---

题意

给定一个BST，其中有两个结点的值互换了导致这个BST不符合定义。要求找到这两个结点并处理使满足BST的性质，同时不能改变树的结构。

思路

BST的性质：中序遍历得到一个单调递增的序列。

最简单的O(N)空间的方法是先用中序遍历得到序列，找到互换了的两个结点，再将它们换回来。

O(1)空间方法：不能使用常规的递归或栈的方法进行中序遍历，改用Morris遍历，中途找到互换的两个结点。

---

代码实现

Java

中序遍历 - O(N)空间

class Solution {
    public void recoverTree(TreeNode root) {
        List<TreeNode> nodes = new ArrayList<>();
        inorder(root, nodes);
        TreeNode A = null, B = null;

        for (int i = 1; i < nodes.size(); i++) {
            if (nodes.get(i).val < nodes.get(i - 1).val) {
                if (A == null) {
                    A = nodes.get(i - 1);
                }
                B = nodes.get(i);
            }
        }

        int tmp = A.val;
        A.val = B.val;
        B.val = tmp;
    }

    private void inorder(TreeNode root, List<TreeNode> nodes) {
        if (root == null) {
            return;
        }

        inorder(root.left, nodes);
        nodes.add(root);
        inorder(root.right, nodes);
    }
}

Morris遍历 - O(1)空间

class Solution {
    public void recoverTree(TreeNode root) {
        TreeNode A = null, B = null;
        TreeNode pre = null;

        while (root != null) {
            if (root.left != null) {
                TreeNode node = root.left;
                while (node.right != null && node.right != root) {
                    node = node.right;
                }
                if (node.right == null) {
                    node.right = root;
                    root = root.left;
                    continue;
                } else {
                    node.right = null;
                }
            }
            if (pre != null && root.val < pre.val) {
                if (A == null) {
                    A = pre;
                }
                B = root;
            }
            pre = root;
            root = root.right;
        }

        int tmp = A.val;
        A.val = B.val;
        B.val = tmp;
    }
}