0589. N-ary Tree Preorder Traversal (E)

N-ary Tree Preorder Traversal (E)

题目

Given the root of an n-ary tree, return the preorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

Example 1:

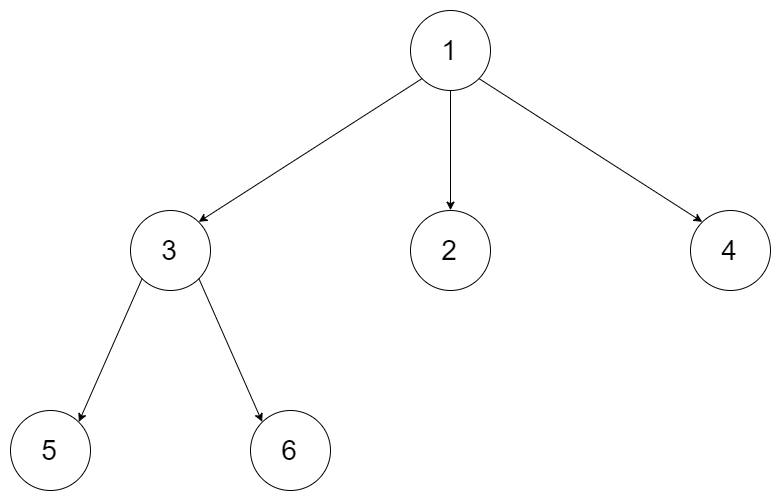
Input: root = [1,null,3,2,4,null,5,6]
Output: [1,3,5,6,2,4]

Example 2:

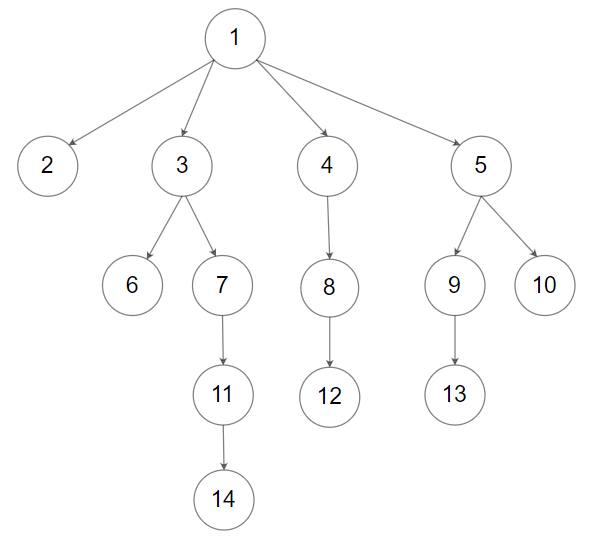
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,2,3,6,7,11,14,4,8,12,5,9,13,10] 

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• 0 <= Node.val <= 10^4
• The height of the n-ary tree is less than or equal to 1000.

Follow up: Recursive solution is trivial, could you do it iteratively?

---

题意

实现对一个随机叉树的前序遍历。

思路

递归或迭代。

---

代码实现

Java

递归

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> list = new ArrayList<>();
        dfs(root, list);
        return list;
    }
    
    private void dfs(Node root, List<Integer> list) {
        if (root == null) return;
        
        list.add(root.val);
        for (Node child : root.children) {
            dfs(child, list);
        }
    }
}

迭代

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> list = new ArrayList<>();
        Deque<Node> stack = new ArrayDeque<>();
        
        if (root != null) stack.push(root);
        
        while (!stack.isEmpty()) {
            Node cur = stack.pop();
            list.add(cur.val);
            for (int i = cur.children.size() - 1; i >= 0; i--) {
                stack.push(cur.children.get(i));
            }
        }
        
        return list;
    }
}