已知直线$l:x+y-sqrt{3}=0$过椭圆$E:dfrac{x^2}{a^2}+dfrac{y^2}{b^2}=1,(a>b>0)$的右焦点且与椭圆$E$交于$A,B$两点,$P$为$AB$中点,$OP$的斜率为$dfrac{1}{2}$.
(1)求椭圆$E$的方程;
(2)设$CD$是椭圆$E$的动弦,且其斜率为$1$,问椭圆$E$上是否存在定点$Q$,使得直线$QC,QD$的斜率分别为$k_1,k_2$满足$k_1+k_2=0?$若存在,求出$Q$的坐标;若不存在,请说明理由.

分析:(1)$c=sqrt{3},k_{op}*k_l=-dfrac{b^2}{a^2}$,易得$a^2=6,b^2=3$故$E:dfrac{x^2}{6}+dfrac{y^2}{3}=1$
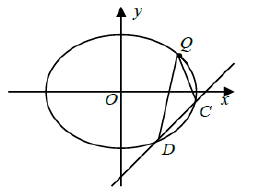
(2)特殊方法.设椭圆切线为$x-y+m=0$,切点为$M(x_0,y_0)$则$6+3-m^2=0$得$m^2=9$,又由椭圆的垂经定理得$k_{OM}*1=-dfrac{3}{6}$故$dfrac{y_0}{x_0}=-dfrac{1}{2}$又$x_0-y_0+m=0$
解得$M(2,-1)vee M(-2,1)$从而$Q(2,1)vee Q(-2,-1)$
一般方法见最后附录:
相关内容:2014辽宁卷21题.
已知圆(x^2+y^2=4)的切线与(x)轴正半轴,(y)轴正半轴围成一个三角形.当该三角形的面积最小时切点为(P).双曲线(C_1:dfrac{x^2}{a^2}-dfrac{y^2}{b^2}=1)过点(P)且离心率为(sqrt 3)
(1)求(C_1)的方程;
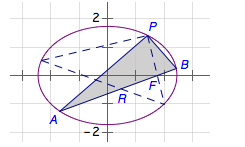
(2)椭圆(C_2)过点(P)且与(C_1)有相同的焦点,直线(l)过(C_2)的右焦点$F$且与(C_2)交于(A),(B)两点.若以线段(AB)为直径的圆过点(P),求(l)的方程.
解答:
(1)(x^2-dfrac {y^2}2=1)
(2)不难得到[C_2:dfrac{x^2}6+dfrac{y^2}3=1.] (P(sqrt 2,sqrt 2)),接下来,我们以(P)为原点,水平方向为(x)轴向重新建立平面直角坐标系,则新坐标系下的椭圆方程为 [dfrac{(x+sqrt 2)^2}6+dfrac{(y+sqrt 2)^2}3=1.] 整理得[dfrac 16x^2+dfrac 13y^2+dfrac{sqrt 2}3x+dfrac{2sqrt 2}3y=0.]
设直线(mx+ny=1)被椭圆截得的弦对(P)的张角为直角,则齐次化联立,有[dfrac 16x^2+dfrac 13y^2+left(dfrac{sqrt 2}3x+dfrac{2sqrt 2}3y
ight)cdot (mx+ny)=0.] 从而有[dfrac 16+dfrac 13+dfrac{sqrt 2}3m+dfrac{2sqrt 2}3n=0.] 整理得[-dfrac{2sqrt 2}3m-dfrac{4sqrt 2}3n=1.] 因此该直线恒过点(Rleft(-dfrac{2sqrt 2}3,-dfrac{4sqrt 2}3
ight)).则原直线恒过$left(dfrac{sqrt 2}3,-dfrac{sqrt 2}3
ight)$
故直线$RF:y=dfrac{3sqrt{6}+2}{25}(x-sqrt{3})$和直线$PF:y=-(2+sqrt{6})(x-sqrt{3})$
(注意:很容易遗漏直线$PF$, 事实上此时$A$ 点与$P$ 点重合)为所求.
注:1.椭圆$dfrac{x^2}{a^2}+dfrac{y^2}{b^2}=1$与直线$AX+BY+C=0$相切则$a^2A^2+b^2B^2-C^2=0$
2.涉及到椭圆上一个定点引出的两条弦的斜率$k_1,k_2$的和与乘积问题一般平移齐次化会出奇制胜.
3.涉及到椭圆里的弦的中点想到两个东西1.点差法 2.椭圆的垂经定理(可由点差法证明)
4.此题如果用仿射变换也可得到类似做法.
附一般做法:

