二叉树（python3版）

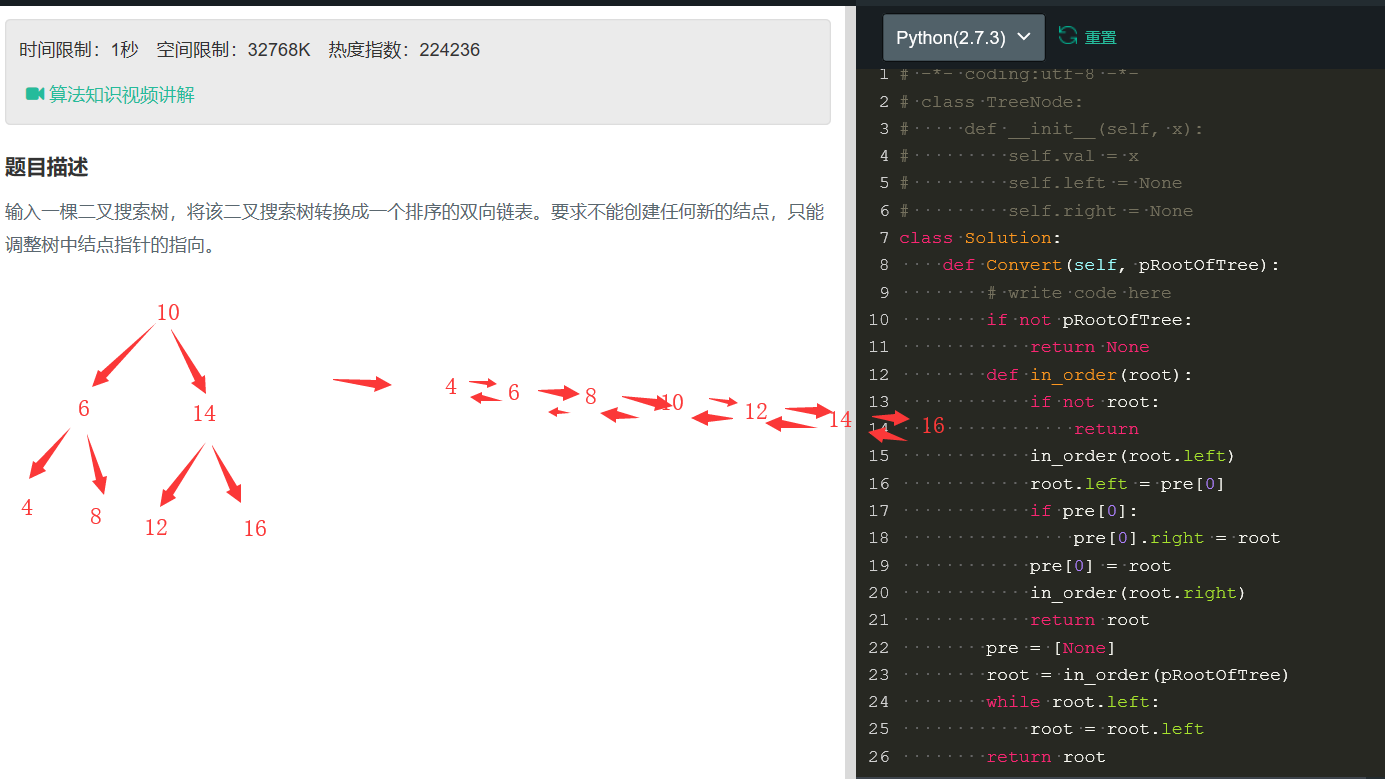
1.二叉树定义特点：

定义：二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。它是树中的一种。

特点：

1）树中每个节点最多只能有两棵树，即每个节点的度最多为2。（ps；度也就是叶子的概念）

2）二叉树的子树有左右之分，即左子树与右子树，次序不能颠倒。

3）二叉树即使只有一个子树时，也要区分是左子树还是右子树。

这里说一下特殊的几种二叉树：斜树（左斜树与右斜树）、满二叉树、完全二叉树。具体百度或者看（大话数据结构）。完全二叉树可以理解为满二叉树少一点点。这两种树的深度比较容易计算。

1.1 满二叉树

  满二叉树作为一种特殊的二叉树，它是指：所有的分支节点都存在左子树与右子树，并且所有的叶子节点都在同一层上。其特点有：
  （1）叶子节点只能出现在最下面一层
  （2）非叶子节点度一定是2
  （3）在同样深度的二叉树中，满二叉树的节点个数最多，节点个数为： 2^h−1 ，其中 h 为树的深度。

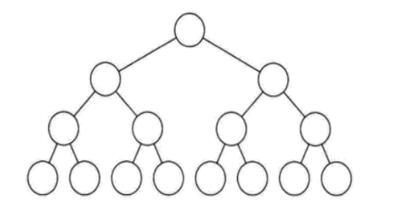
1.2 完全二叉树

  若设二叉树的深度为 h ，除第 h 层外，其它各层 (1～h−1)的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。其具有以下特点：
  （1）叶子节点可以出现在最后一层或倒数第二层。
  （2）最后一层的叶子节点一定集中在左部连续位置。
  （3）完全二叉树严格按层序编号。（可利用数组或列表进行实现，满二叉树同）
  （4）若一个节点为叶子节点，那么编号比其大的节点均为叶子节点。

　　这两个的深度计算可以统称为：！log₂n！+1，其中！x！这个符号定义为不大于x的意思。n是结点数。

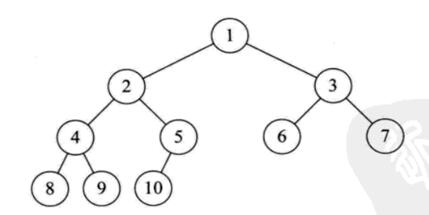
2.二叉树的建立

暂且看这个（以后碰到好的或者例子改）

3.二叉树的五种遍历

常见的五种遍历：前序遍历、中序遍历、后序遍历，层次遍历，深度优先遍历，看这里。 

以下遍历以该二叉树为例：

 

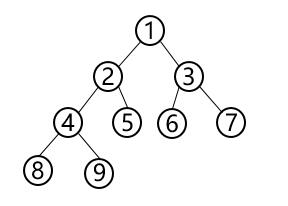
3.1 前序遍历

  思想：先访问根节点，再先序遍历左子树，然后再先序遍历右子树。总的来说是根—左—右
  上图先序遍历结果为为：1,2,4,8,9,5,3,6,71,2,4,8,9,5,3,6,7
  代码如下：

    def PreOrder(self, root):
        '''打印二叉树(先序)'''
        if root == None:
            return 
        print(root.val, end=' ')
        self.PreOrder(root.left)
        self.PreOrder(root.right)

3.2 中序遍历

  思想：先中序访问左子树，然后访问根，最后中序访问右子树。总的来说是左—根—右
  上图中序遍历结果为为：8,4,9,2,5,1,6,3,78,4,9,2,5,1,6,3,7
  代码如下：

    def InOrder(self, root):
        '''中序打印'''
        if root == None:
            return
        self.InOrder(root.left)
        print(root.val, end=' ')
        self.InOrder(root.right)

3.3 后序遍历

  思想：先后序访问左子树，然后后序访问右子树，最后访问根。总的来说是左—右—根
  上图后序遍历结果为为：8,9,4,5,2,6,7,3,18,9,4,5,2,6,7,3,1
  代码如下：

    def BacOrder(self, root):
        '''后序打印'''
        if root == None:
            return
        self.BacOrder(root.left)
        self.BacOrder(root.right)
        print(root.val, end=' ')

3.4 层次遍历（宽度优先遍历）

  思想：利用队列，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历。
  上图后序遍历结果为为：1,2,3,4,5,6,7,8,91,2,3,4,5,6,7,8,9
  代码如下：

    def BFS(self, root):
        '''广度优先'''
        if root == None:
            return
        # queue队列，保存节点
        queue = []
        # res保存节点值，作为结果
        #vals = []
        queue.append(root)

        while queue:
            # 拿出队首节点
            currentNode = queue.pop(0)
            #vals.append(currentNode.val)
            print(currentNode.val, end=' ')
            if currentNode.left:
                queue.append(currentNode.left)
            if currentNode.right:
                queue.append(currentNode.right)
        #return vals

3.5 深度优先遍历

  思想：利用栈，先将根入栈，再将根出栈，并将根的右子树，左子树存入栈，按照栈的先进后出规则来实现深度优先遍历。
  上图后序遍历结果为为：1,2,4,8,9,5,3,6,71,2,4,8,9,5,3,6,7
  代码如下：

    def DFS(self, root):
        '''深度优先'''
        if root == None:
            return
        # 栈用来保存未访问节点
        stack = []
        # vals保存节点值，作为结果
        #vals = []
        stack.append(root)

        while stack:
            # 拿出栈顶节点
            currentNode = stack.pop()
            #vals.append(currentNode.val)
            print(currentNode.val, end=' ')
            if currentNode.right:
                stack.append(currentNode.right)
            if currentNode.left:
                stack.append(currentNode.left)          
        #return vals

3.6 代码运行结果

 

4.二叉树一道剑指上的例题：

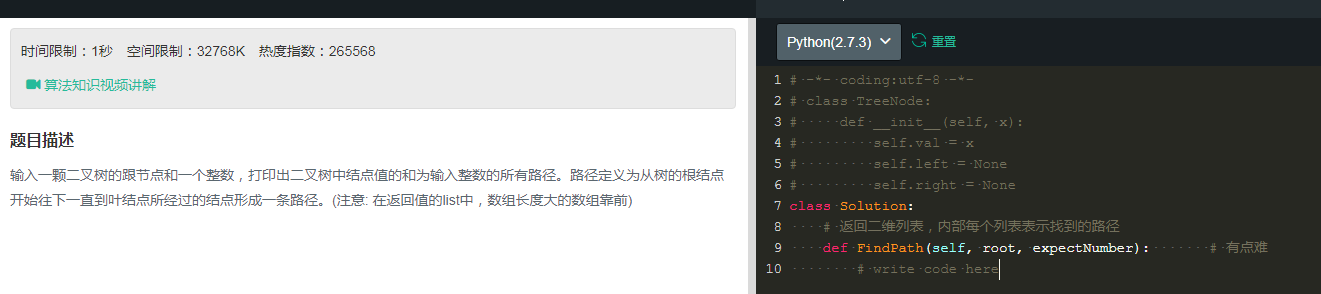
解题与调试全代码：

#!/usr/bin/env python
#-*-coding:utf-8 -*-


class Node(object):
    def __init__(self, number):
        self.val = number
        self.left = None
        self.right = None


class Tree(object):
    lis = []

    def __init__(self):
        self.root = None

    def add(self, number):
        node = Node(number)

        if self.root == None:
            self.root = node
            Tree.lis.append(self.root)
        else:
            while True:
                point = Tree.lis[0]

                if point.left == None:
                    point.left = node
                    Tree.lis.append(point.left)
                    return
                elif point.right == None:
                    point.right = node
                    Tree.lis.append(point.right)
                    Tree.lis.pop(0)
                    return


    #先序遍历函数
    def preOrderTrave(self, bt):
        if bt is not None:
            print(bt.val, end=" ")
            self.preOrderTrave(bt.left)
            self.preOrderTrave(bt.right)

def FindPath(root, expectNumber):
    # write code here
    if not root:
        return []
    if root and not root.left and not root.right and root.val == expectNumber:
        return [[root.val]]
    res = []
    print(root.val,expectNumber)
    left = FindPath(root.left, expectNumber-root.val)
    right = FindPath(root.right, expectNumber-root.val)
    for i in left+right:
        res.append([root.val]+i)
    return res


if __name__ == '__main__':
    t = Tree()
    data_list = [10,5,12,4,7]
    for x in data_list:
        t.add(x)
    t.preOrderTrave(t.root)

    # 以上是创建书中的二叉树，下面是解题
    res = FindPath(t.root, 22)
    print(res)