快速排序改进——3区快速排序（3-way quicksort）

1.快速排序缺陷

　　快速排序面对重复的元素时的处理方法是，把它放在了左部分数组或右部分数组，下次进行分区时，还需检测它。如果需要排序的数组含有大量重复元素，则这个问题会造成性能浪费。

　　解决方法：新增一个相同区域，并把重复元素放进去，下次进行分区时，不对相同区域进行分区。

2. 3区快速排序（3-way quicksort）

　　从例子入手：

　　

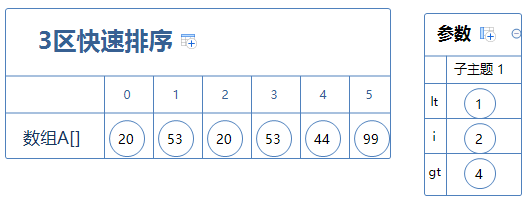
　　现有数组A[]如上图。

　　令int lt=0; int i =1; int gt=5;

　　首先从A[0]（53）开始　　

　　A[lt]与A[i]进行对比，结果：A[0]<A[1], 交换A[i]与A[gt], gt减一：

　　

　　A[lt]与A[i]进行对比，结果：A[0]>A[1], 交换A[i]与A[lt], lt加一，i加一：

 　　

　　A[lt]与A[i]进行对比，结果：A[1]>A[2],交换A[i]与A[lt], lt加一，i加一：

　　

　　A[lt]与A[i]进行对比，结果：A[2]=A[3],i加一：

　　

　　A[lt]与A[i]进行对比，结果：A[1]>A[2],交换A[i]与A[lt], lt加一，i加一：

　　

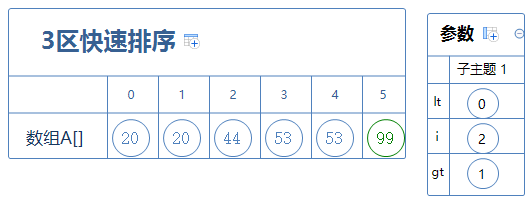
　　i>gt,第一次排序结束。

　　此时，整个数组分为3个区：

　　第一个区里的所有数字都比53小，它含有a[0]~a[2];

　　第二个区里的所有数字都等于53，它含有a[3]~a[4];

　　第三个的所有数字都比53大，它含有a[5];

　　我们还需要对第一个区和第三个区进行3区快速排序（因为这两个区里的数字可能还是乱的，虽然在本例中顺序是对的）

　　从第一个区的第一个数字20开始：

　　令int lt=0; int i =1; int gt=2;

　　

　　A[lt]与A[i]进行对比，结果：A[2]=A[3],i加一：

　　

　　A[lt]与A[i]进行对比，结果：A[0]<A[2], 交换A[i]与A[gt], gt减一：（这里i=gt，所以等于没交换）

 　　

　　i>gt,第二次排序结束。

　　此时，整个区分为3个区：

　　第一个区里的所有数字都比20小，它没有元素;

　　第二个区里的所有数字都等于20，它含有a[0]~a[1];

　　第三个的所有数字都比20大，它含有a[2];

　　对第一个区和第三个区进行3区快速排序，但第一个区没元素，不用排；第三个区只有一个元素，不用排。

　　

　　对下一个区进行3区快速排序，但此区只有A[5]一个元素，不用排；

　　没有下一个区了，排序结束。

　　总结一下：

　　对于一个数组A[]，令lt=0;i=1，gt为数组的最后一个元素的序号（index）。

　　1.从A[lt]开始，如果A[lt]>A[i]，交换lt项元素和i项元素，lt++,i++；如果A[lt]=A[i], i++；如果A[lt]<A[i]，交换gt项元素和i项元素，gt--。

　　2.当i>gt时，数组已经分好3个区域了。

　　3.对大于A[lt]的元素区域和小于A[lt]的元素区域分别进行3区快速排序，直到分区数组只有一个元素为止。

3.实现代码

.h:

UCLASS()
class ALGORITHM_API AThreeWayQuicksort : public AActor
{
    GENERATED_BODY()
    
public:    
    // Sets default values for this actor's properties
    AThreeWayQuicksort();
    // Called every frame
    virtual void Tick(float DeltaTime) override;

    //生成数组
    void InitArray(int N);
    //更换数组里两个数字
    void ExChange(int i, int j);
    //开始排序
    void Sort();
    void Sort(int lo, int hi);
protected:
    // Called when the game starts or when spawned
    virtual void BeginPlay() override;

public:    
    

private:
    TArray<int> MyIntArray;
};

.cpp:

// Sets default values
AThreeWayQuicksort::AThreeWayQuicksort()
{
     // Set this actor to call Tick() every frame.  You can turn this off to improve performance if you don't need it.
    PrimaryActorTick.bCanEverTick = true;
}

// Called when the game starts or when spawned
void AThreeWayQuicksort::BeginPlay()
{
    Super::BeginPlay();
    //测试
    //生成数组
    InitArray(1000);
    UKismetSystemLibrary::PrintString(this, "Before Sort: ");
    for (int i = 0; i < MyIntArray.Num(); i++)
    {
        UKismetSystemLibrary::PrintString(this, FString::FromInt(i) + " : " + FString::FromInt(MyIntArray[i]));
    }
    //开始排序
    Sort();
    UKismetSystemLibrary::PrintString(this, "After Sort: ");
    for (int i = 0; i < MyIntArray.Num(); i++)
    {
        UKismetSystemLibrary::PrintString(this, FString::FromInt(i) + " : " + FString::FromInt(MyIntArray[i]));
    }
}

// Called every frame
void AThreeWayQuicksort::Tick(float DeltaTime)
{
    Super::Tick(DeltaTime);
}

void AThreeWayQuicksort::InitArray(int N)
{
    FRandomStream Stream;
    Stream.GenerateNewSeed();
    for (int i = 0; i < N; i++)
    {
        MyIntArray.Add(Stream.RandRange(0, 100));
    }
}

void AThreeWayQuicksort::ExChange(int i, int j)
{
    //序号i,j应该在数组范围内
    if (i > MyIntArray.Num() - 1 || j > MyIntArray.Num() - 1) return;
    //互换
    int Tempint = MyIntArray[i];
    MyIntArray[i] = MyIntArray[j];
    MyIntArray[j] = Tempint;
}

void AThreeWayQuicksort::Sort()
{
    Sort(0, MyIntArray.Num() - 1);
}

void AThreeWayQuicksort::Sort(int lo, int hi)
{
    if (hi <= lo) return;
    //left是小于V和等于V的分界线
    int Left(lo);
    //Right是大于V和等于V的分界线
    int Right(hi);
    int V(MyIntArray[lo]);
    //i是等于V和未排序元素的分界线
    int i(lo);
    while (i <= Right)
    {
        //如果小于V,放在Left的左边（小于V的元素区间）
        if (MyIntArray[i] < V) ExChange(Left++, i++);
        //如果大于V,放在Right的右边（大于V的元素区间）
        else if (MyIntArray[i] > V) ExChange(i, Right--);
        //如果等于V,i++，相当于放在Left和i之间（等于V的元素区间）
        else i++;
    }
    //然后这两部分数组作为新的部分数组继续分下去，直到hi <= lo
    Sort(lo, Left - 1);
    Sort(Right + 1, hi);
}