阅读《C语言编程—一本全面的C语言入门教程》一书,看到了质数生成的小程序,特此记录
1. 直接求解
这是最简单和无脑的暴力算法了,直接双重循环,复杂度为(O(N^2)):
void prime_generator_1(void)
{
int p;
int d;
bool isPrime;
for( p = 2; p <= MAX_NUM; ++p)
{
isPrime = true;
for( d = 2; d < p; ++ d)
{
if(p % d == 0)
{
isPrime = 0;
break;
}
}
if( isPrime != false)
{
printf("%i ", p);
}
}
printf("
");
}
2. 一些改进
很明显的一个改进是,任何大于2的偶数都不可能是质数,因此,在外循环中p从3开始,每次递增2;内循环与之类似。额外注意的是,2既是偶数,也是质数,需单独处理。
void prime_generator_2(void)
{
int p;
int d;
bool isPrime;
printf("%i ", 2);
for( p = 3; p <= MAX_NUM; p += 2)
{
isPrime = true;
for( d = 3; d < p; d += 2)
{
if(p % d == 0)
{
isPrime = 0;
break;
}
}
if( isPrime != false)
{
printf("%i ", p);
}
}
printf("
");
}
3. 继续改进
以上的改进虽然有效,但算法的效率并没有根本性的提高,特别是在产生大型的质数表(>1,000,000),算法的效率至关重要。
有两个标准可以帮助提高效率
- 任何一个非质整数都可以分解为多个质数的乘积,也就是说,如果一个数不能被任何质数整除,那么这个数就是一个质数。
- 任何一个非质数的整数,肯定会有一个小于其平方根的质因数。
void prime_generator_3(void)
{
int primes[MAX_NUM];
int primeIndex = 2;
bool isPrime;
primes[0] = 2;
primes[1] = 3;
for( int p = 5; p <= MAX_NUM; p += 2)
{
isPrime = true;
for( int i = 1; isPrime && primes[i] <= sqrt(p); ++i)
{
if(p % primes[i] == 0)
{
isPrime = false;
break;
}
}
if( isPrime == true)
{
primes[primeIndex ++] = p;
}
}
for(int i = 0; i < primeIndex; ++ i)
{
printf("%i ", primes[i]);
}
printf("
");
}
4. 埃拉托色尼筛网法
其步骤为:
- 定义整数数组
P, 将所有的数组元素设置为0. - 设置变量
i等于2。 - 如果
i > n,算法结束。 - 如果
P[i]等于0, 那么i是一个质数。 - 对于所有的正整数
j, 如果i * j <= n,将数组元素P[i*j]设置为1。 - 将
i的值增加1,返回第3步。
代码如下:
void prime_generator_4(void)
{
int primes[MAX_NUM + 1] ={0};
int i = 2;
while(i <= MAX_NUM)
{
if(primes[i] == 0)
{
printf("%i ", i);
}
for( int j = 2; i * j <= MAX_NUM; ++j)
{
primes[i * j] = 1;
}
++i;
}
printf("
");
}
5. 对比
当MAX_NUM =500000 时,前三种算法的计算时长分别为:
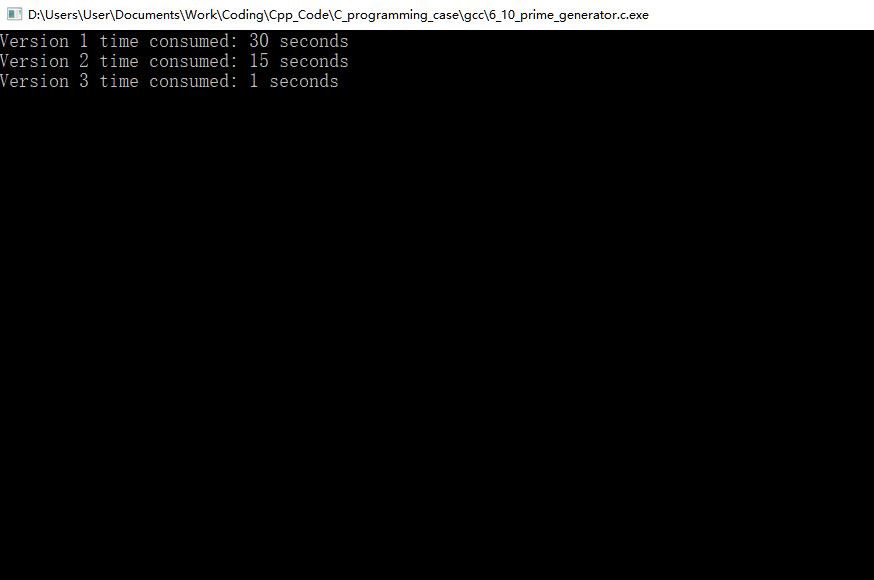
可以看到,经过改进,算法的时间消耗得到大幅降低,表明改进算法的有效性。
6. 关于数组越界带来的死循环问题
这个问题在第4部分代码编写过程中出现过,后来经过搜索找到了原因,数组越界导致循环变量被重新赋值。其汇编代码如下:

在此验证了一个简单的C语言数组循环语句,对循环变量和数组越界元素的地址进行了输出,可以看到,二者地址一致,证明了以上的论断。
