hdu 4947

GCD Array

Time Limit: 11000/5500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1765    Accepted Submission(s): 559

Problem Description

Teacher Mai finds that many problems about arithmetic function can be reduced to the following problem:

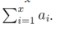
Maintain an array a with index from 1 to l. There are two kinds of operations:

  1. Add v to a_x for every x that gcd(x,n)=d.
  2. Query 

 

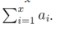
Input

There are multiple test cases, terminated by a line "0 0".

For each test case, the first line contains two integers l,Q(1<=l,Q<=5*10^4), indicating the length of the array and the number of the operations.

In following Q lines, each line indicates an operation, and the format is "1 n d v" or "2 x" (1<=n,d,v<=2*10^5,1<=x<=l).

 

Output

For each case, output "Case #k:" first, where k is the case number counting from 1.

Then output the answer to each query.

 

Sample Input

6 4

1 4 1 2

2 5

1 3 3 3

2 3

0 0

 

Sample Output

Case #1:

6 7

 

析：长度为n的序列，初始为0，有2种操作：

　　1.输入n，d，v，对序列中元素ax加上v，其中x满足gcd(n，x) = d

　　2.输入x，查询1-x前缀和

　　给所有满足gcd(n，x) = d的数加上v 等价于[gcd(n，x) == d]*v 等价于  [gcd(n/d，x/d) == 1]*v

　　于是由莫比乌斯反演公式a_i=$sumlimits_{d|i}^{n} f(d)$ ，于是 a_x += $v imes[gcd(x/d,n/d)=1]$ = a_x+=$v imes sumlimits_{p|frac{n}{d},p|frac{x}{d}}mu(p)$，

　　发现枚举n/d的所有因数的d倍就是添加操作会影响的f数组的位置，所以添加f(pd) += $v∗μ(p)$

　　查询时，a[x]= $sumlimits_{d|x}f(d)$= $sumlimits_{i=1}^{x}f(d)  sumlimits_{d|x}f(d)$，而$sumlimits_{d|x}f(d)$部分可对d进行枚举，即$sumlimits_{d=1}^{x}frac{x}{d}f(d)$，

　　然后针对$frac{x}{d}$进行分块

 

#include <math.h>
#include <vector>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 200005;
int t, n, m, ans;
int mo[N], prm[N], isP[N];
ll a[N];
vector<int>f[N];
void Mobius(){
    ans = mo[1] = 1;
    for(int i = 2; i < N; i ++){
        if(!isP[i]){
            prm[ans++] = i;
            mo[i] = -1;
        }
        for(int j = 1; j < ans; j ++){
            int tmp = i*prm[j];
            if(tmp >= N)break;
            isP[tmp] = 1;
            if(i%prm[j] == 0){
                mo[tmp] = 0;
                break;
            }else{
                mo[tmp] = -mo[i];
            }
        }
    }
    for(int i = 1; i < N; i ++){
        for(int j = i; j < N; j += i)
            f[j].push_back(i);
    }
}
void add(int x, int v){
    while(x <= n){
        a[x] += v;
        x += x&(-x);
    }
}
ll sum(int x){
    ll res = 0;
    while(x > 0){
        res += a[x];
        x -= x&(-x);
    }
    return res;
}
void update(int x, int d, int v){
    if(x%d)
        return;
    x /= d;
    for(int i = 0; i < f[x].size(); i ++){
        int q = f[x][i];
        add(q*d, mo[q]*v);
    }
}
ll query(int x){
    ll res = 0;
    for(int l = 1, r; l <= x; l = r+1){
        r = x/(x/l);
        res += x/l*(sum(r)-sum(l-1));
    }
    return res;
}
int main(){
    Mobius();
    int x, d, v, op, tot = 1;
    while(scanf("%d%d", &n, &m)){
        if(n+m == 0)
            break;
        fill(a, a+n+1, 0);
        printf("Case #%d:
", tot++);
        while(m--){
            scanf("%d", &op);
            if(op&1){
                scanf("%d%d%d", &x, &d, &v);
                update(x, d, v);
            }else{
                scanf("%d", &x);
                printf("%I64d
", query(x));
            }
        }
    }
    return 0;
}