1.一些逻辑比较复杂的题用离散数学来撸逻辑,逻辑就会很清楚了,就不会有错
https://www.cnblogs.com/conw/p/5896155.html
1.暴力法
复杂度O(N^3)。假设数组长度为N。因为有3个嵌套的循环,每个循环最大可能次数与n的一次方成线性关系。
1 public static int B(int[] a){ 2 int n= a.length;//获取数组长度 3 int maxSum=a[0];//最大和初始化为数组第一个值 4 int currSum;//当前子序列的和 5 //设i为子序列头,j为子序列尾,那么没一对i,j就对应一个子序列。 6 // 用两个嵌套的循环来确定每一对i,j 7 for(int i=0;i<n;i++){ 8 for(int j=i;j<n;j++){ 9 currSum=0;//初始化当前子序列和为0 10 // 下面的这个循环用于求一对i,j确定的子序列的和 11 for(int k=i;k<=j;k++){ 12 currSum+=a[k]; 13 } 14 // 如果该子序列的和大于最大和就更新最大和 15 if(currSum>maxSum){ 16 maxSum=currSum; 17 } 18 } 19 } 20 //返回最大和 21 return maxSum; 22 }

2.分治法:时间复杂度T(n)=O(nlogn);n为数组长度。
最多可能递归的次数与n成线性,所以为logn,每次递归里面有一个循环(该循环与n成线性,所以为n),即时间复杂度为nlogn
1 /** 2 * 最大连续子数列和(接口无法统一,因为要用到递归)-分治法 3 * @param a 4 * @return 5 */ 6 /* 7 分治法思路: 8 这个最大和子序列的元素要么 9 A:全在中点左边 10 B:全在中点的右边 11 C:一部分在左边一部分在右边 12 如果是C情况,是能够简单直接求出最大和的, 13 C求最大和方法: 14 左边部分向左扩展为和最大的子序列,右边部分向右扩展为和最大 15 的子序列,然后相加即可(这个扩展的复杂度为n)。 16 如果为A(或B):调用函数递归左(或右)子序列即可。 17 三种情况的最大子序列都求出来。 18 最后比较三种情况求出来的值哪个最大,哪个就是最大子序列了 19 */ 20 21 //from表示递归的数组的首元素下标,to表示尾元素下标, 22 // 实质上由下标构建出一个子数组来递归。 23 public static int B2(int[] a,int from,int to){ 24 //下标相等说明只有一个元素,直接返回 25 if(from==to){ 26 return a[from]; 27 } 28 //求出中点 29 int middle=(from+to)/2; 30 // 全在中点左边。递归 31 int s1=A2.B2(a, from, middle); 32 // 全在中点的右边。递归 33 int s2=A2.B2(a,middle+1,to); 34 // 一部分在左边一部分在右边 35 //求左边部分最大和 36 int left=a[middle]; 37 int currSum=a[middle]; 38 for(int i=middle-1;i>=from;i--){ 39 currSum+=a[i]; 40 if(currSum>left){ 41 left=currSum; 42 } 43 } 44 //求右边部分最大和 45 int right=a[middle+1]; 46 currSum=a[middle+1]; 47 for(int i=middle+2;i<=to;i++){ 48 currSum+=a[i]; 49 if(currSum>right){ 50 right=currSum; 51 } 52 } 53 int s3=left+right; 54 //比较三种情况的子序列和,返回最大那个 55 //return s1>s2?s1:(s2>s3?s2:s3);这是错误的,只判断s1>s2就返回s1了,但s1不一定>s3啊 56 return (s1>s2 && s1>s3)?s1:(s2>s3?s2:s3); 57 }
3.分析法(注:分析法并不是常规的算法,而是根据实际情况分析出来的算法,所以分析法是没有统一标准和特征的)
通过分析得出了非常简便的方法,且时间复杂度为n(当然因题而异)
分析法和动态规划一样?
4.动态规划法(最优子问题),时间复杂度O(n)。
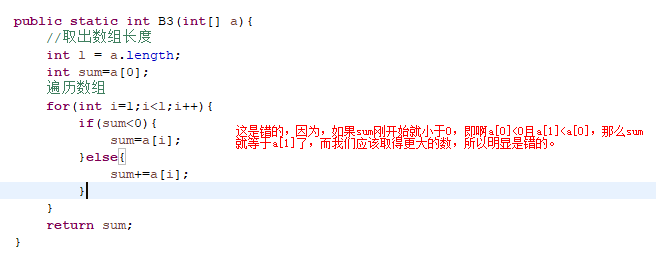
1 /** 2 * 最大连续子数列和(接口统一)-分析法 3 * @param a 4 * @return 5 */ 6 /* 7 分析法思路: 8 分析题目: 9 定义一个sum=首元素,如果sum<0,那么就取sum=sum序列的下一个元素。否则sum+=sum序列的下一个元素。 10 */ 11 12 public static int B3(int[] a){ 13 //取出数组长度 14 int l = a.length; 15 int sum=a[0]; 16 int result=a[0]; 17 // 遍历数组 18 for(int i=1;i<l;i++){ 19 if(sum<0){ 20 //表示舍弃前面相加的和<0的部分 21 sum=a[i]; 22 }else{ 23 sum+=a[i]; 24 } 25 if(sum>result){ 26 result=sum; 27 } 28 } 29 return result; 30 }