案例学习SelfAttention及其实现实现

文章链接

第0步. 什么是self-attention?

原文链接： Transformer 一篇就够了（一）： Self-attenstion

接下来，我们将要解释和实现self-attention的全过程。

• 准备输入
• 初始化参数
• 获取key，query和value
• 给input1计算attention score
• 计算softmax
• 给value乘上score
• 给value加权求和获取output1
• 重复步骤4-7，获取output2，output3

import torch

第1步: 准备输入

为了简单起见，我们使用3个输入，每个输入都是一个4维的向量。

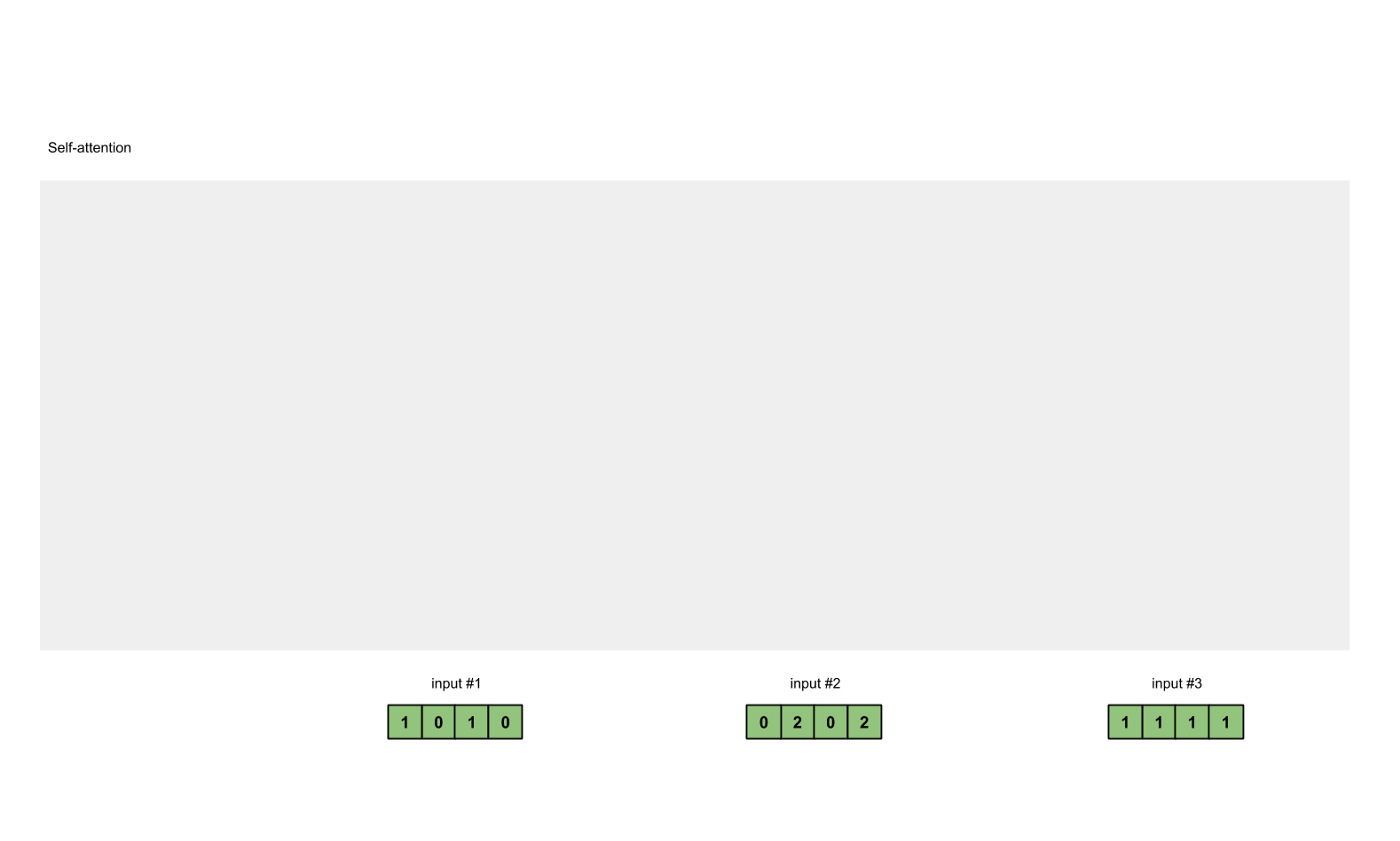
x = [
  [1, 0, 1, 0], # Input 1
  [0, 2, 0, 2], # Input 2
  [1, 1, 1, 1]  # Input 3
 ]
x = torch.tensor(x, dtype=torch.float32)
x

tensor([[1., 0., 1., 0.],
        [0., 2., 0., 2.],
        [1., 1., 1., 1.]])

第2步: 初始化参数

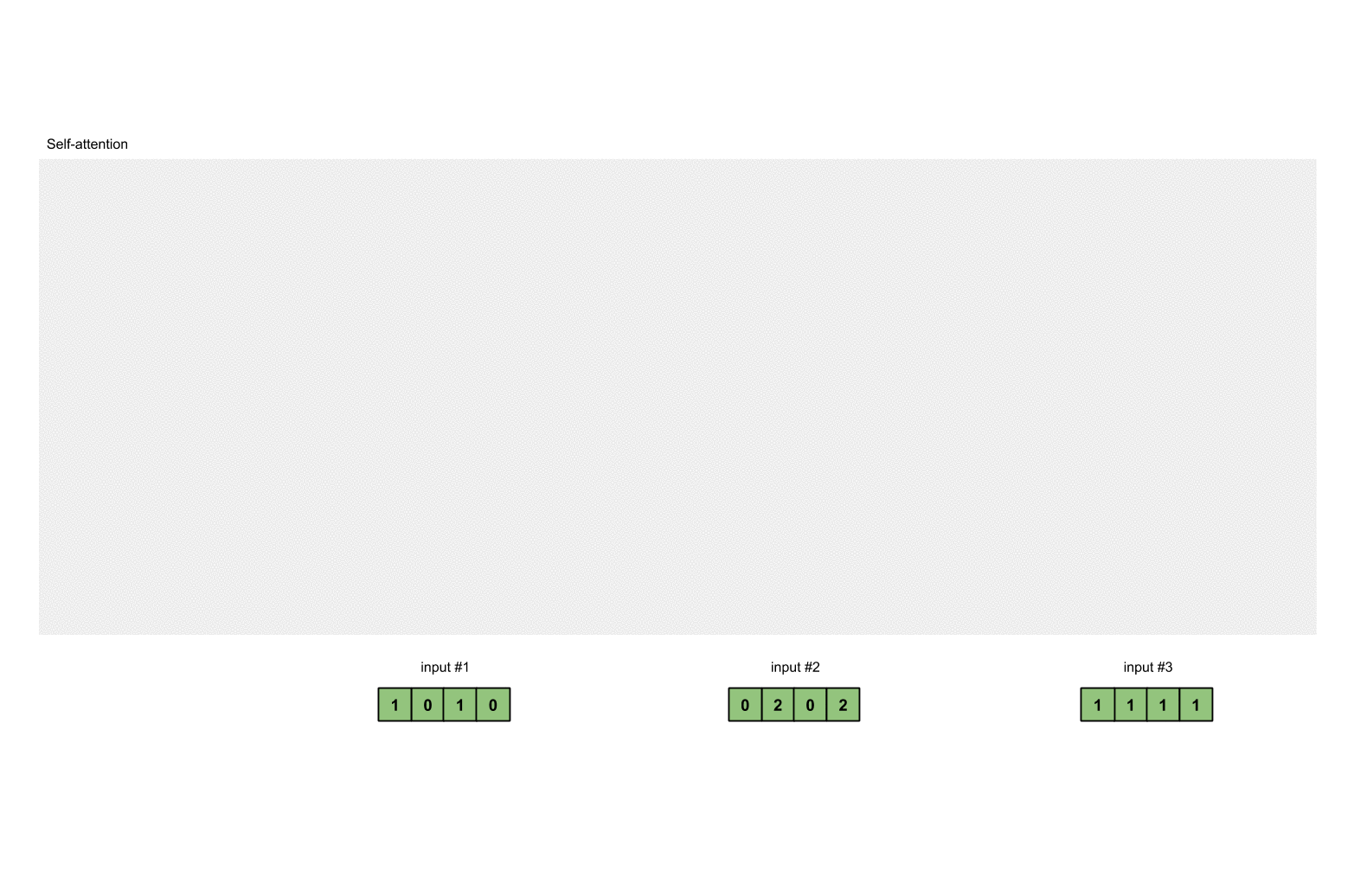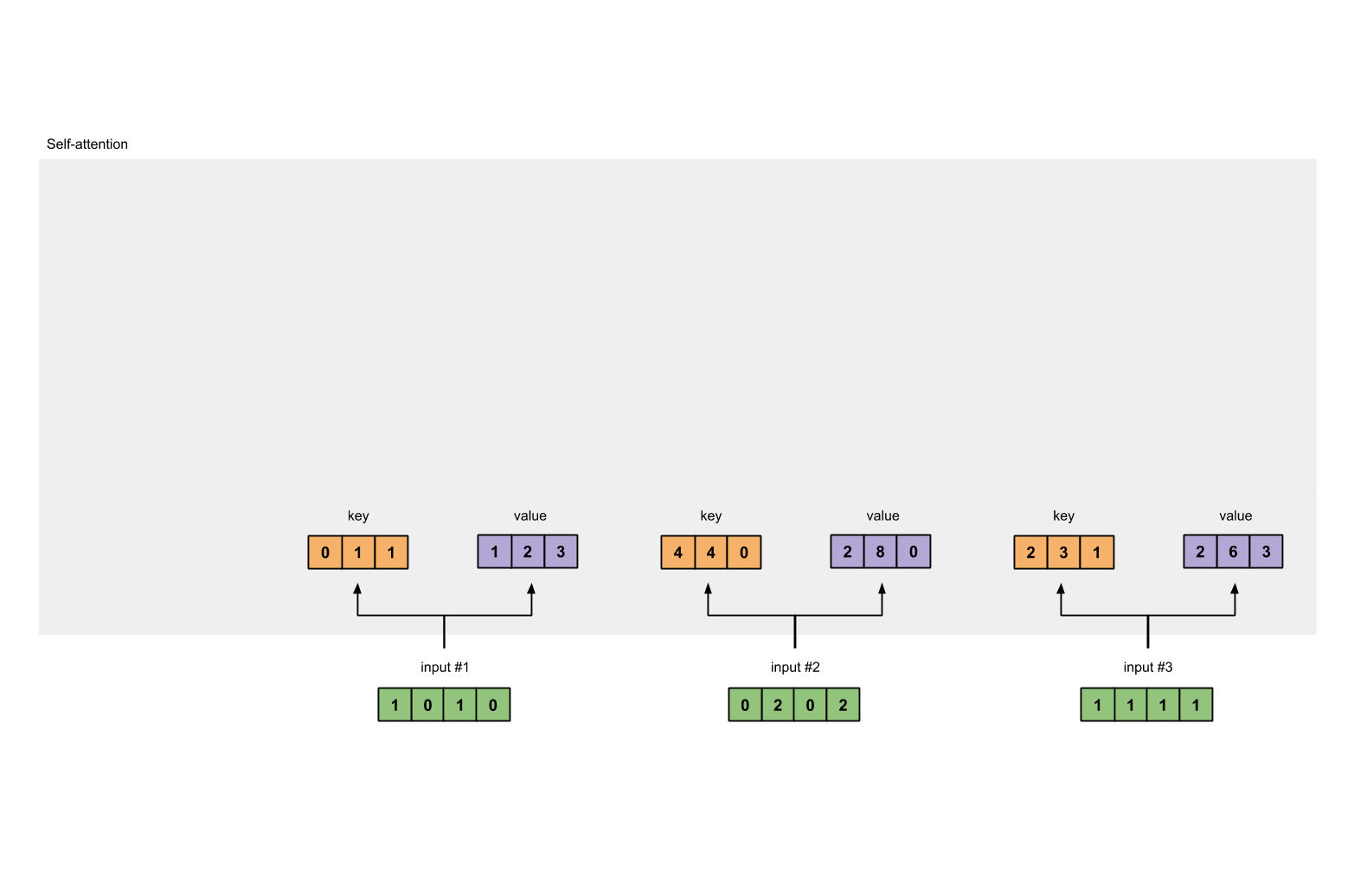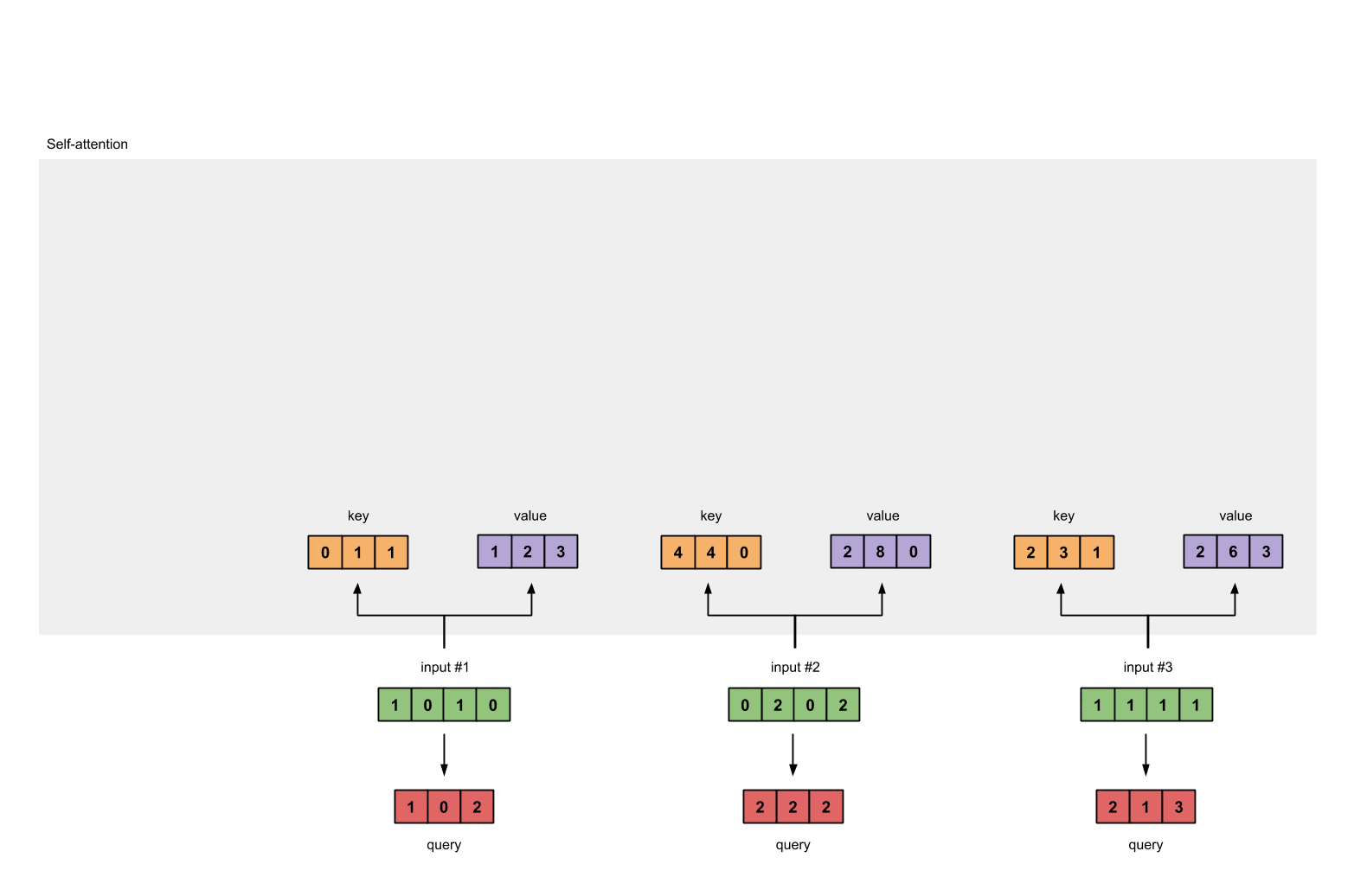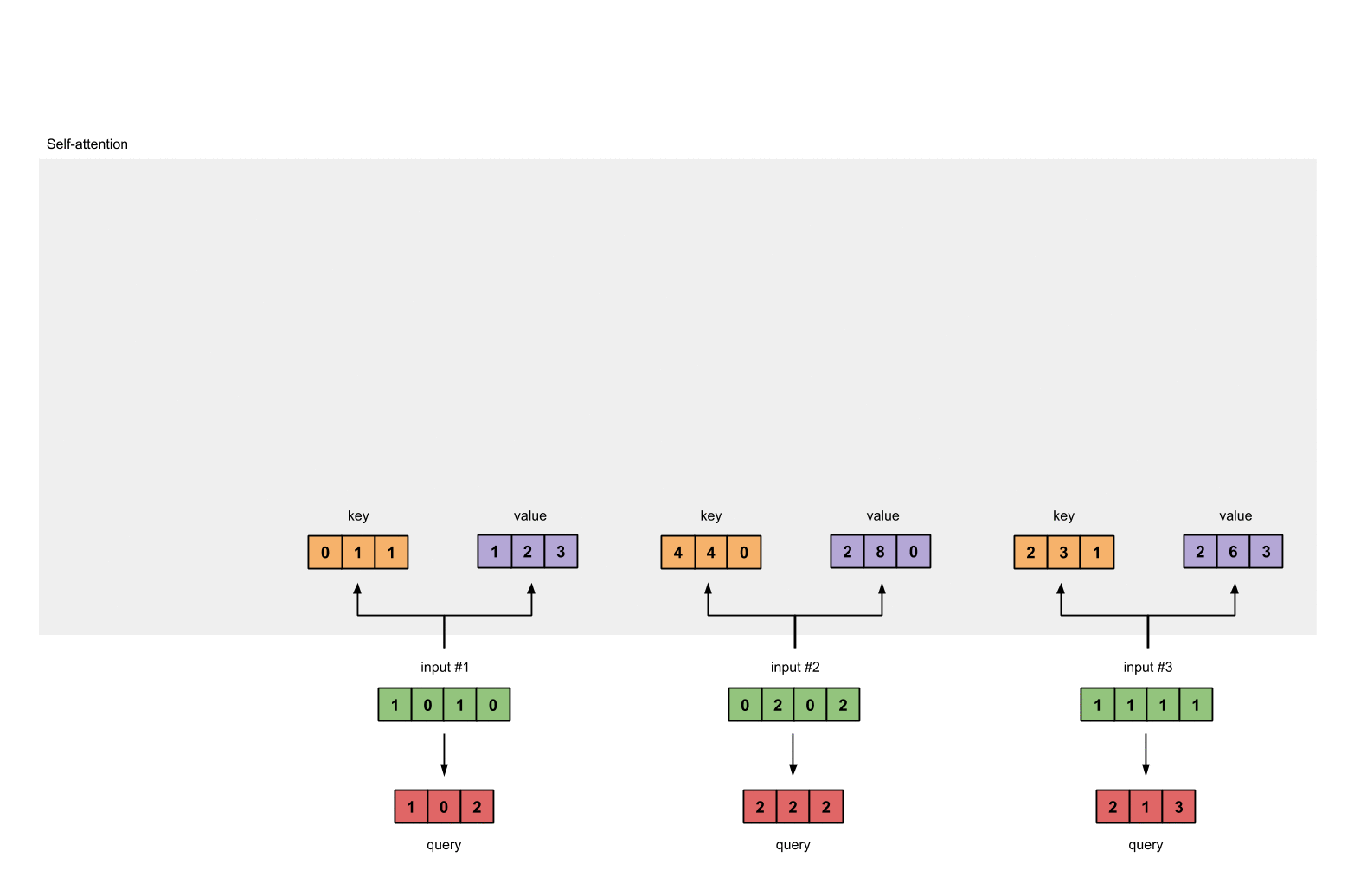
每一个输入都有三个表示，分别为key（橙黄色）query（红色）value（紫色）。比如说，每一个表示我们希望是一个3维的向量。由于输入是4维，所以我们的参数矩阵为 4\times3 维。

后面我们会看到，value的维度，同样也是我们输出的维度。

为了能够获取这些表示，每一个输入（绿色）要和key，query和value相乘，在我们例子中，我们使用如下的方式初始化这些参数。

w_key = [
  [0, 0, 1],
  [1, 1, 0],
  [0, 1, 0],
  [1, 1, 0]
]
w_query = [
  [1, 0, 1],
  [1, 0, 0],
  [0, 0, 1],
  [0, 1, 1]
]
w_value = [
  [0, 2, 0],
  [0, 3, 0],
  [1, 0, 3],
  [1, 1, 0]
]
w_key = torch.tensor(w_key, dtype=torch.float32)
w_query = torch.tensor(w_query, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)

print("Weights for key: \n", w_key)
print("Weights for query: \n", w_query)
print("Weights for value: \n", w_value)

Weights for key: 
 tensor([[0., 0., 1.],
        [1., 1., 0.],
        [0., 1., 0.],
        [1., 1., 0.]])
Weights for query: 
 tensor([[1., 0., 1.],
        [1., 0., 0.],
        [0., 0., 1.],
        [0., 1., 1.]])
Weights for value: 
 tensor([[0., 2., 0.],
        [0., 3., 0.],
        [1., 0., 3.],
        [1., 1., 0.]])

Note: 通常在神经网络的初始化过程中，这些参数都是比较小的，一般会在Gaussian, Xavier and Kaiming distributions随机采样完成。

第3步：获取key，query和value

现在我们有了三个参数，现在就让我们来获取实际上的key，query和value。

keys的表示为：

               [0, 0, 1]
[1, 0, 1, 0]   [1, 1, 0]   [0, 1, 1]
[0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0]
[1, 1, 1, 1]   [1, 1, 0]   [2, 3, 1]

values的表示为：

               [0, 2, 0]
[1, 0, 1, 0]   [0, 3, 0]   [1, 2, 3] 
[0, 2, 0, 2] x [1, 0, 3] = [2, 8, 0]
[1, 1, 1, 1]   [1, 1, 0]   [2, 6, 3]

querys的表示为：

               [1, 0, 1]
[1, 0, 1, 0]   [1, 0, 0]   [1, 0, 2]
[0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2]
[1, 1, 1, 1]   [0, 1, 1]   [2, 1, 3]

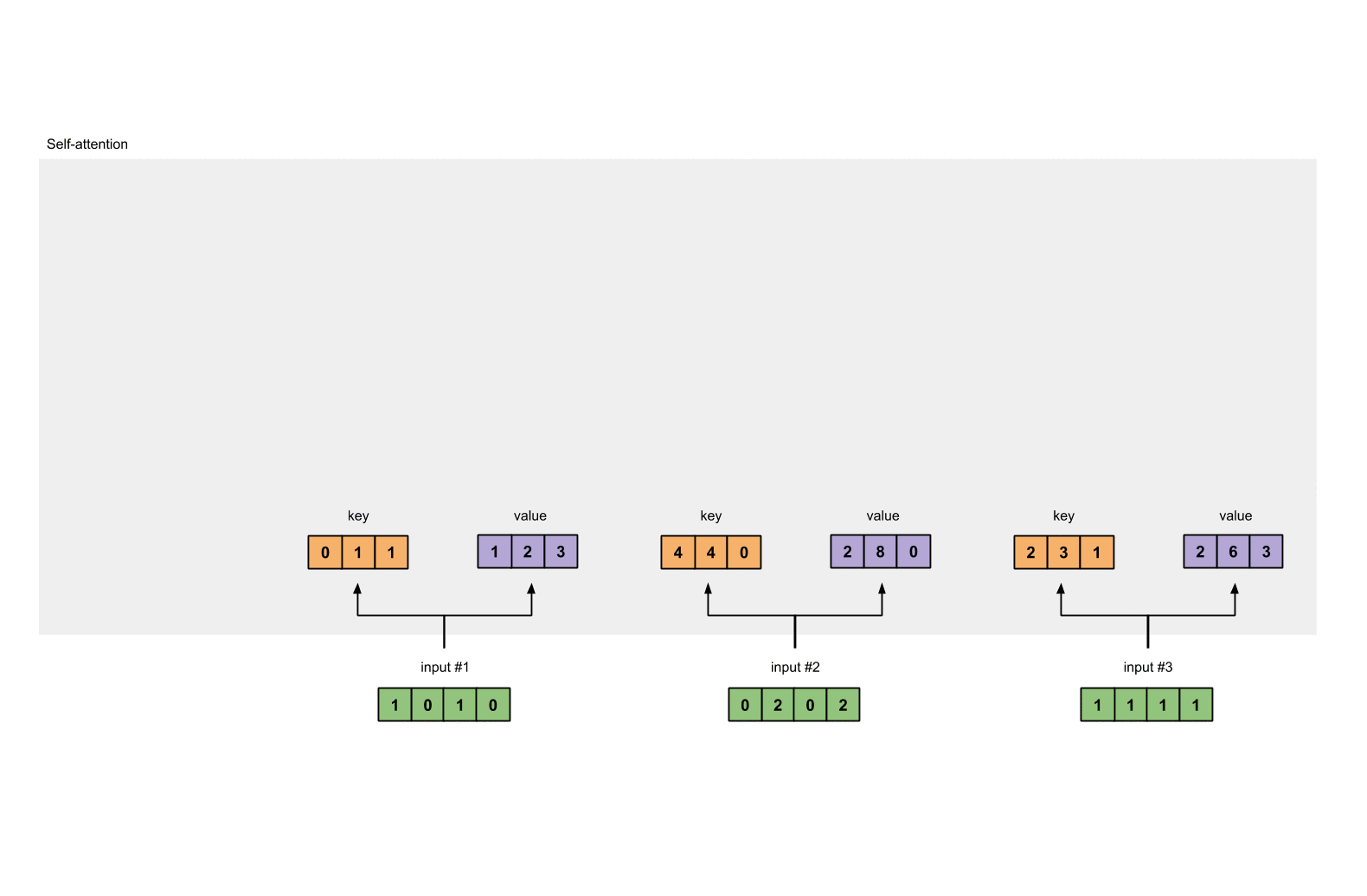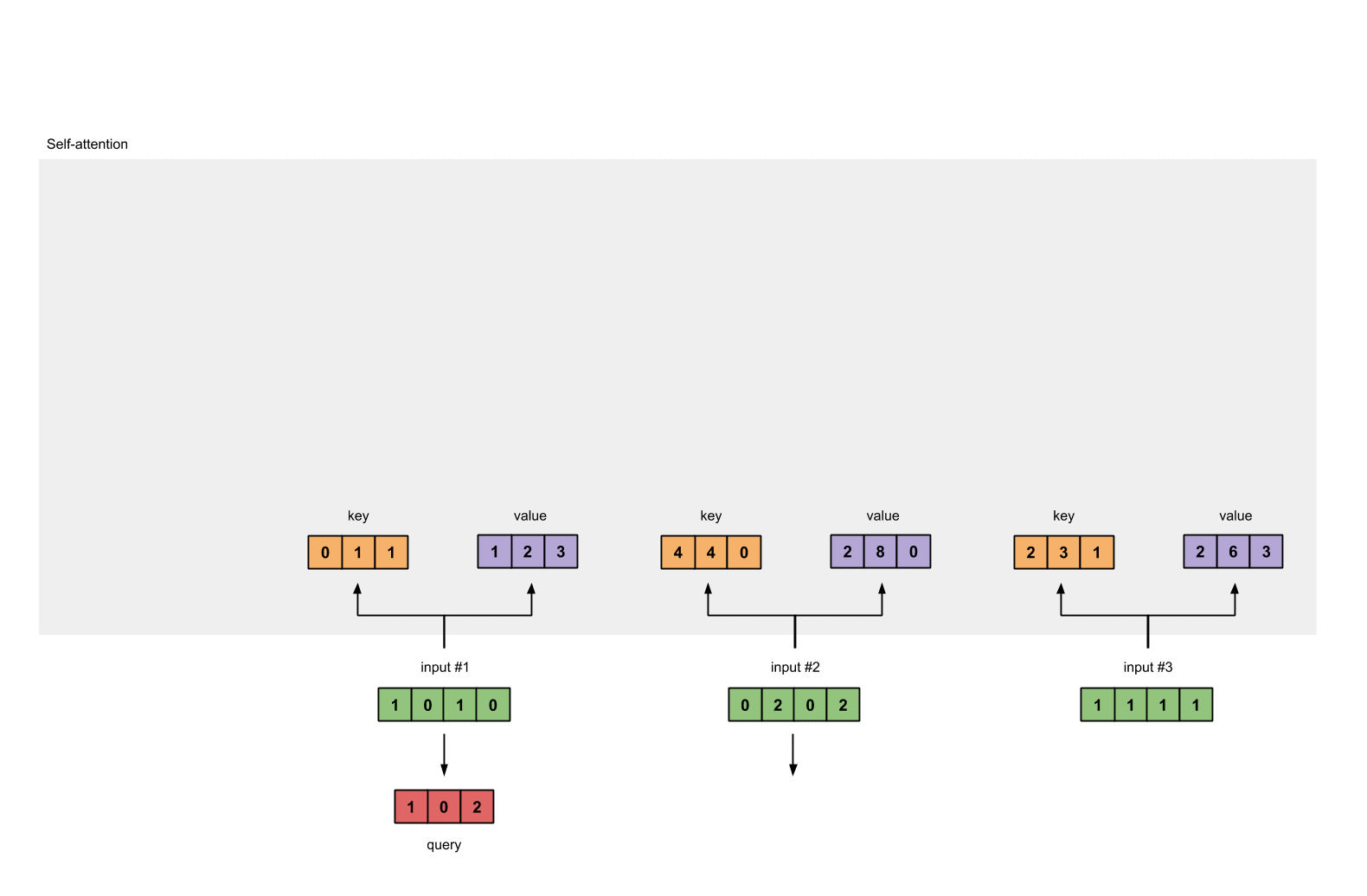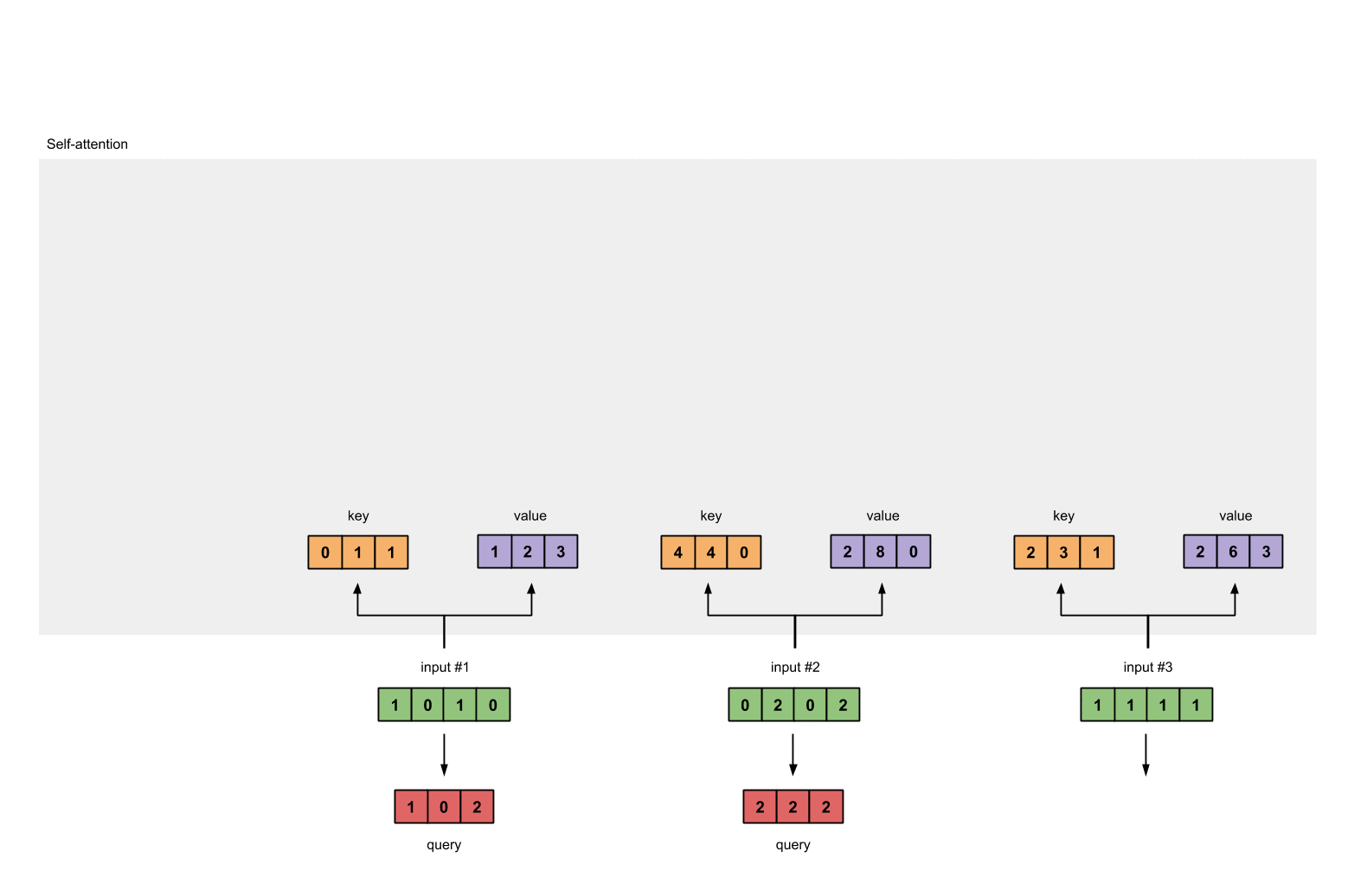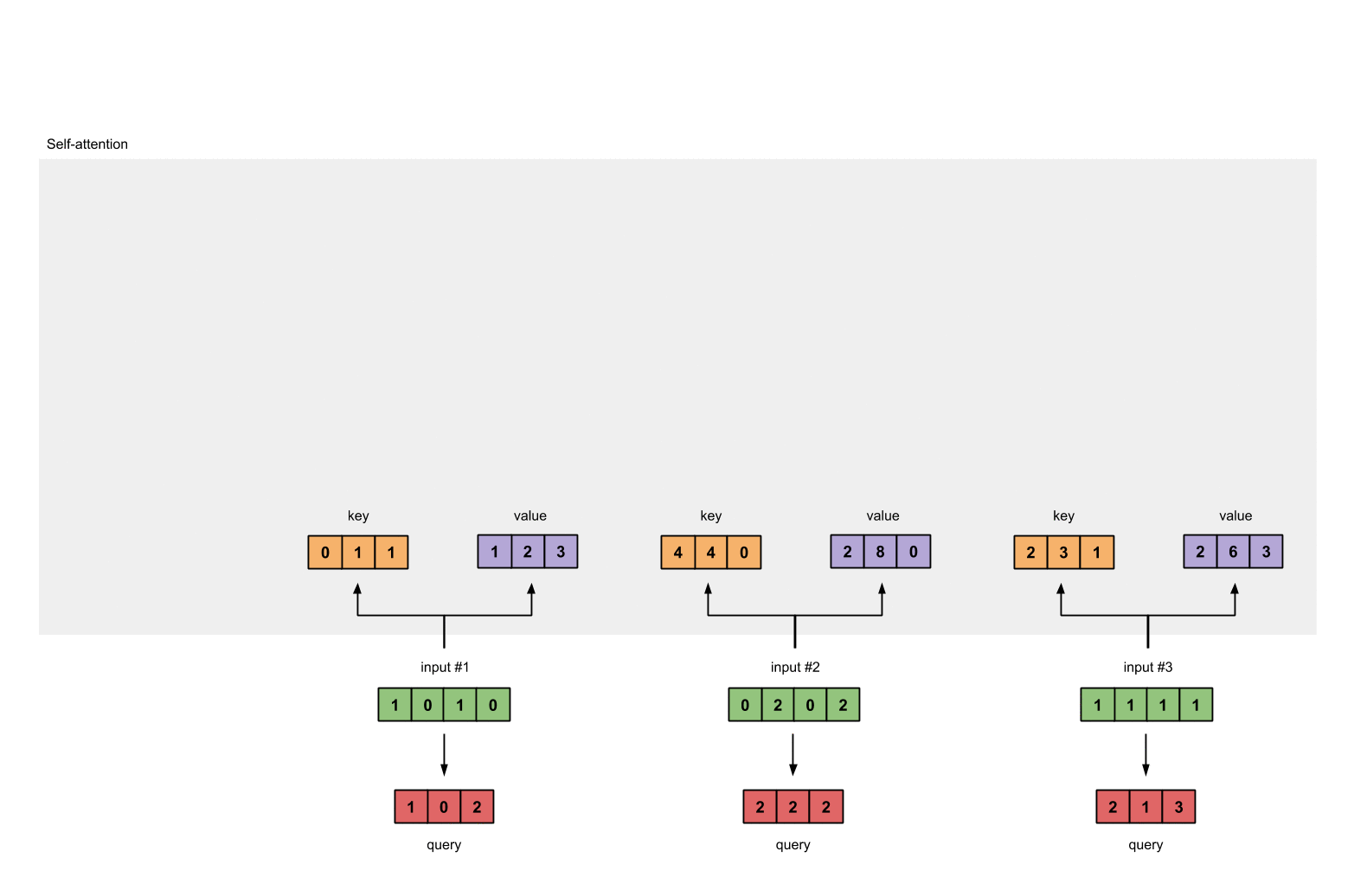
Notes: 在我们实际的应用中，有可能会在点乘后，加上一个bias的向量。

keys = x @ w_key
querys = x @ w_query
values = x @ w_value

print("Keys: \n", keys)
# tensor([[0., 1., 1.],
#         [4., 4., 0.],
#         [2., 3., 1.]])

print("Querys: \n", querys)
# tensor([[1., 0., 2.],
#         [2., 2., 2.],
#         [2., 1., 3.]])
print("Values: \n", values)
# tensor([[1., 2., 3.],
#         [2., 8., 0.],
#         [2., 6., 3.]])

Keys: 
 tensor([[0., 1., 1.],
        [4., 4., 0.],
        [2., 3., 1.]])
Querys: 
 tensor([[1., 0., 2.],
        [2., 2., 2.],
        [2., 1., 3.]])
Values: 
 tensor([[1., 2., 3.],
        [2., 8., 0.],
        [2., 6., 3.]])

第4步: 计算 attention scores

为了获取input1的attention score，我们使用点乘来处理所有的key和query，包括它自己的key和value。这样我们就能够得到3个key的表示（因为我们有3个输入），我们就获得了3个attention score（蓝色）。

            [0, 4, 2]
[1, 0, 2] x [1, 4, 3] = [2, 4, 4]
            [1, 0, 1]

这里我们需要注意一下，这里我们只有input1的例子。后面，我们会对其他的输入的query做相同的操作。

attn_scores = querys @ keys.T
print(attn_scores)

# tensor([[ 2.,  4.,  4.],  # attention scores from Query 1
#         [ 4., 16., 12.],  # attention scores from Query 2
#         [ 4., 12., 10.]]) # attention scores from Query 3

tensor([[ 2.,  4.,  4.],
        [ 4., 16., 12.],
        [ 4., 12., 10.]])

第5步: 计算softmax

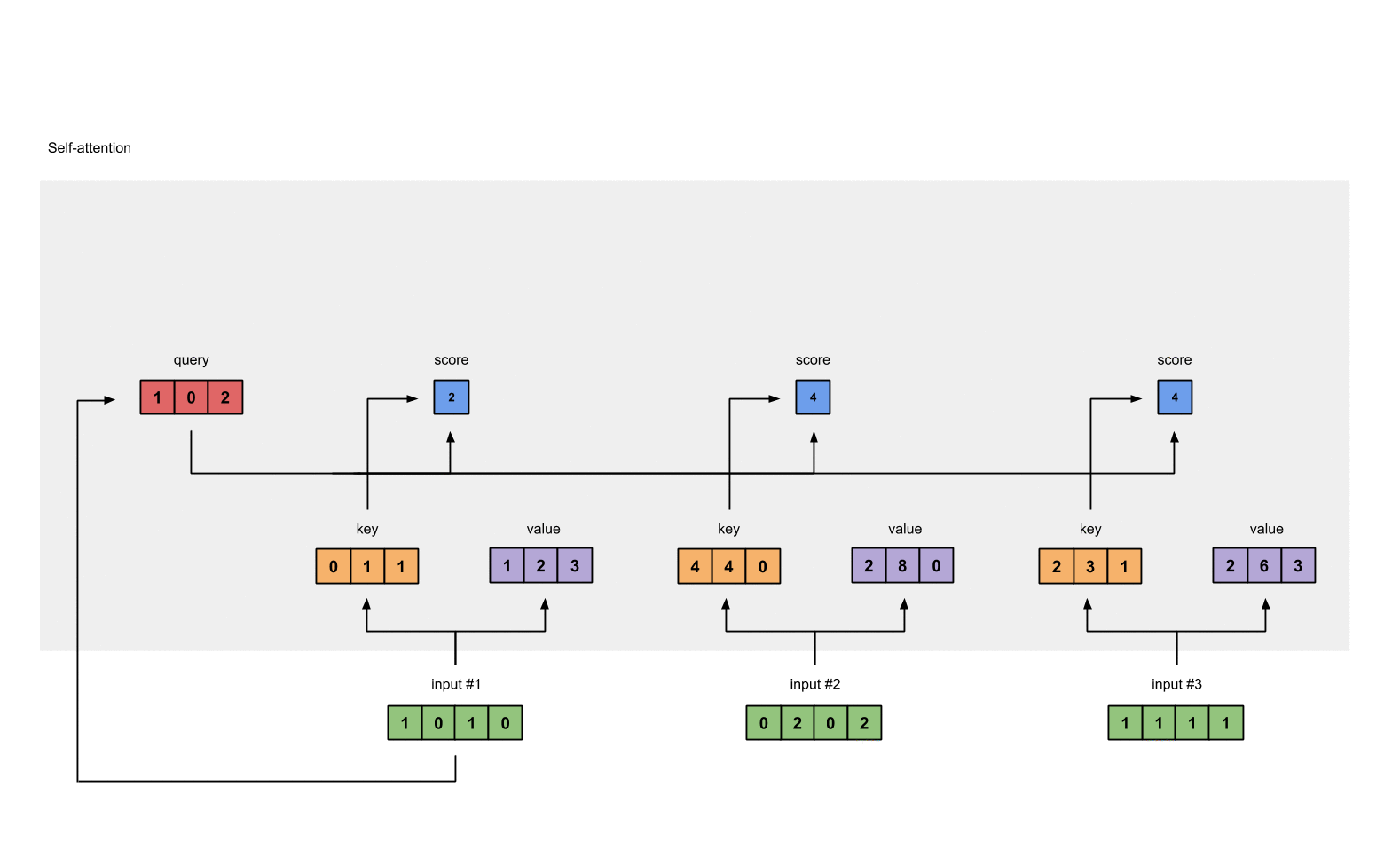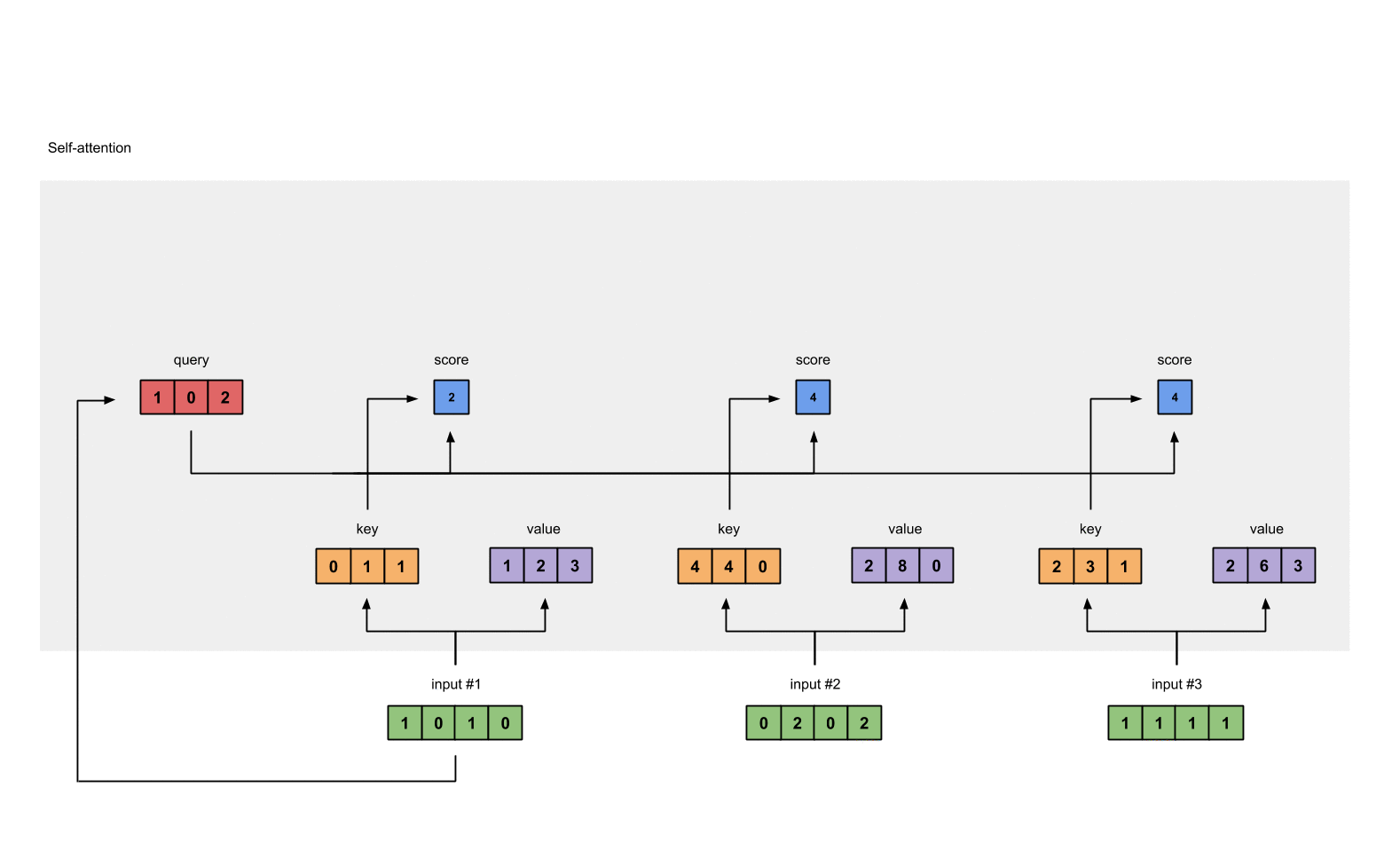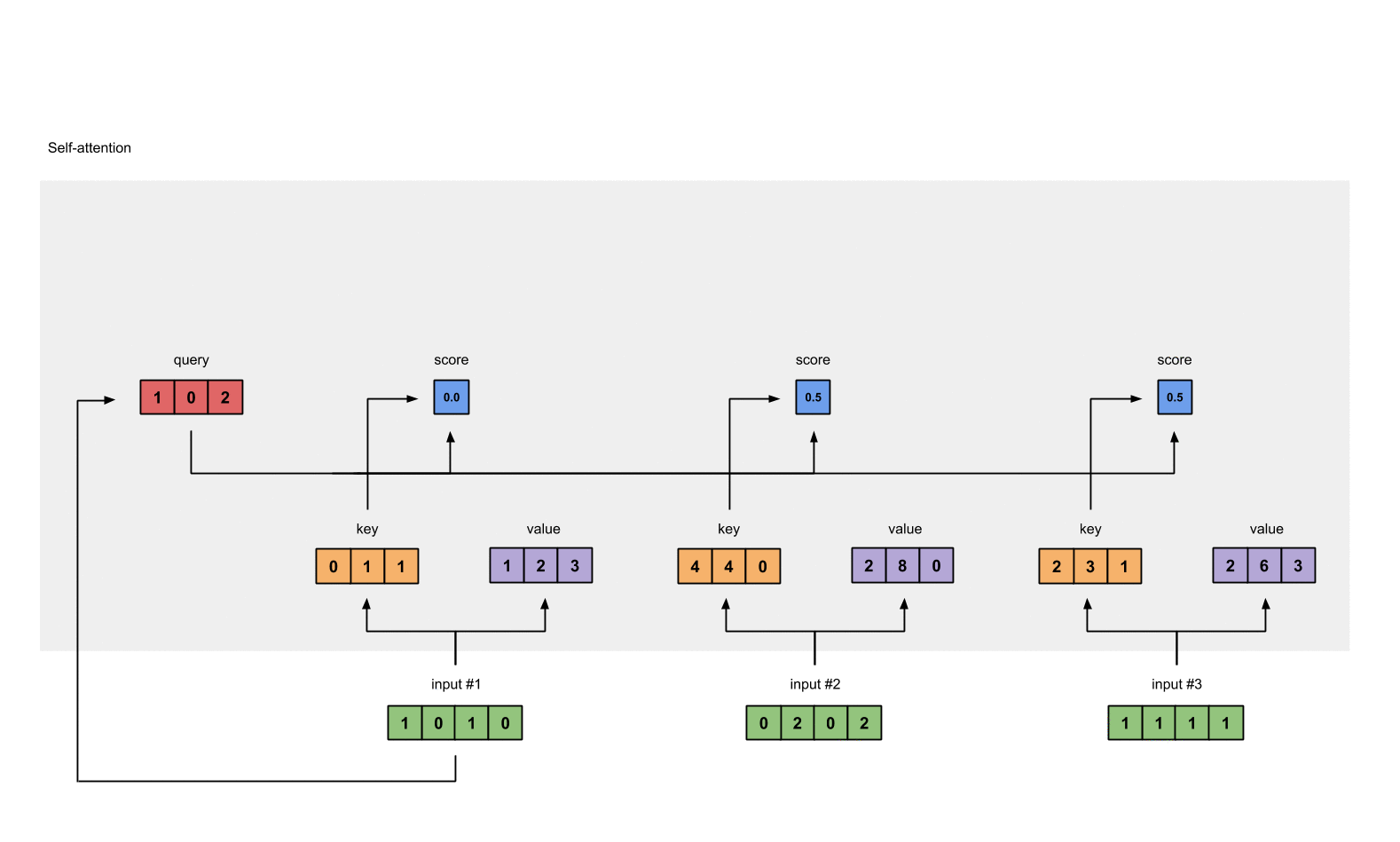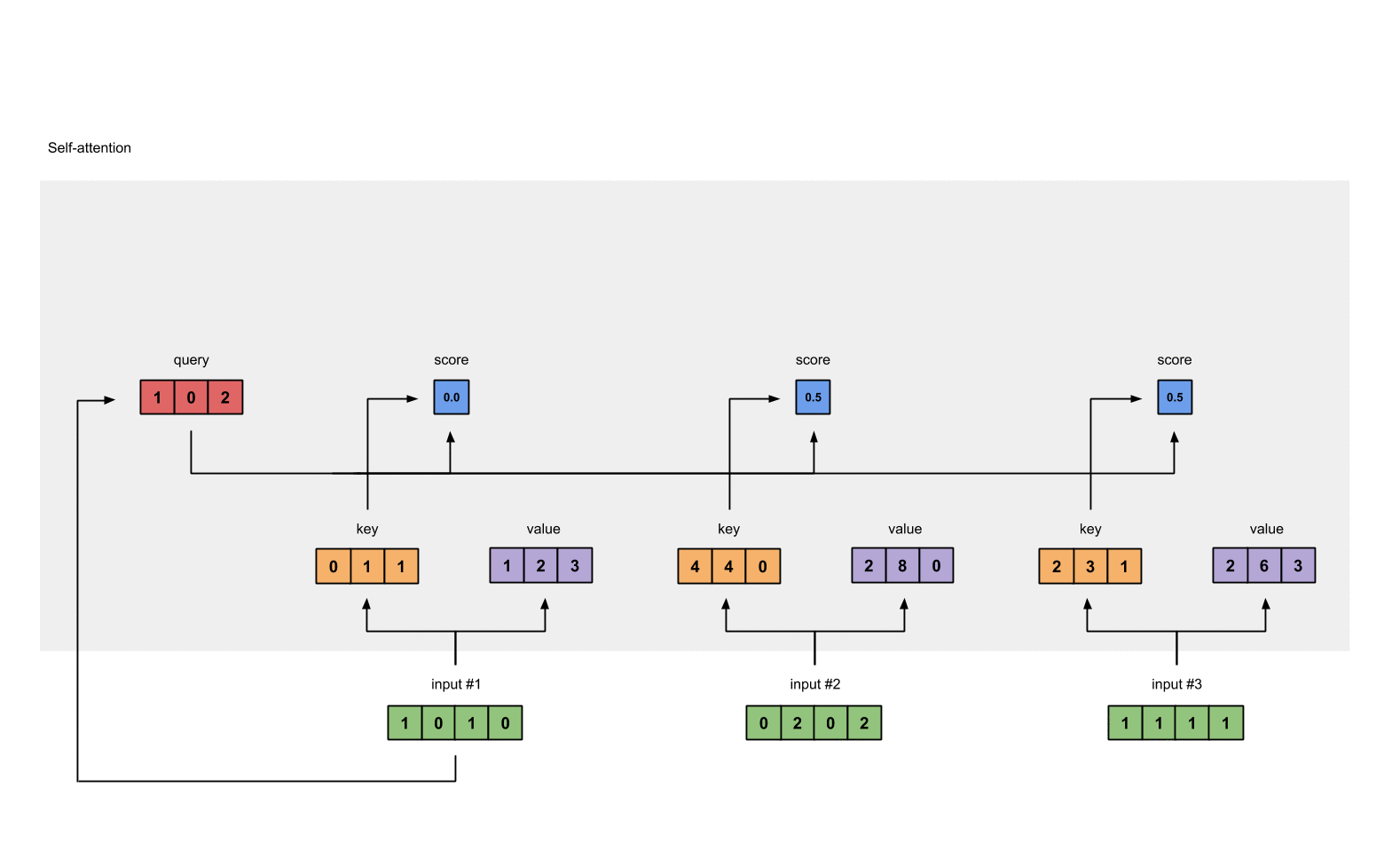
给attention score应用softmax。

softmax([2, 4, 4]) = [0.0, 0.5, 0.5]

from torch.nn.functional import softmax

attn_scores_softmax = softmax(attn_scores, dim=-1)
print(attn_scores_softmax)
# tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
#         [6.0337e-06, 9.8201e-01, 1.7986e-02],
#         [2.9539e-04, 8.8054e-01, 1.1917e-01]])

# For readability, approximate the above as follows
attn_scores_softmax = [
  [0.0, 0.5, 0.5],
  [0.0, 1.0, 0.0],
  [0.0, 0.9, 0.1]
]
attn_scores_softmax = torch.tensor(attn_scores_softmax)
print(attn_scores_softmax)

tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
        [6.0337e-06, 9.8201e-01, 1.7986e-02],
        [2.9539e-04, 8.8054e-01, 1.1917e-01]])
tensor([[0.0000, 0.5000, 0.5000],
        [0.0000, 1.0000, 0.0000],
        [0.0000, 0.9000, 0.1000]])

第6步: 给value乘上score

使用经过softmax后的attention score乘以它对应的value值（紫色），这样我们就得到了3个weighted values（黄色）。

1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]
2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]
3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]

weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]
print(weighted_values)

tensor([[[0.0000, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0000]],

        [[1.0000, 4.0000, 0.0000],
         [2.0000, 8.0000, 0.0000],
         [1.8000, 7.2000, 0.0000]],

        [[1.0000, 3.0000, 1.5000],
         [0.0000, 0.0000, 0.0000],
         [0.2000, 0.6000, 0.3000]]])

第7步: 给value加权求和获取output

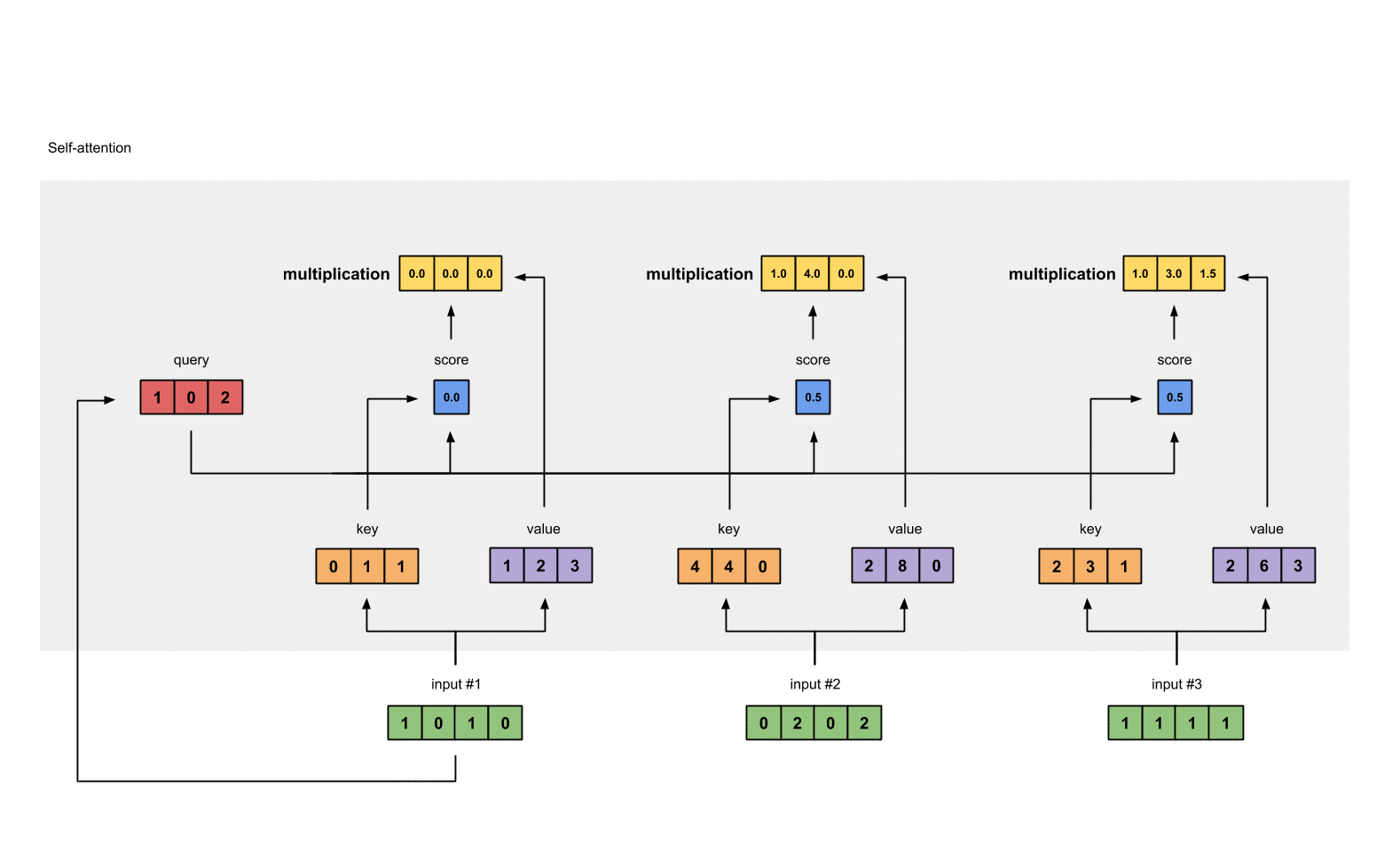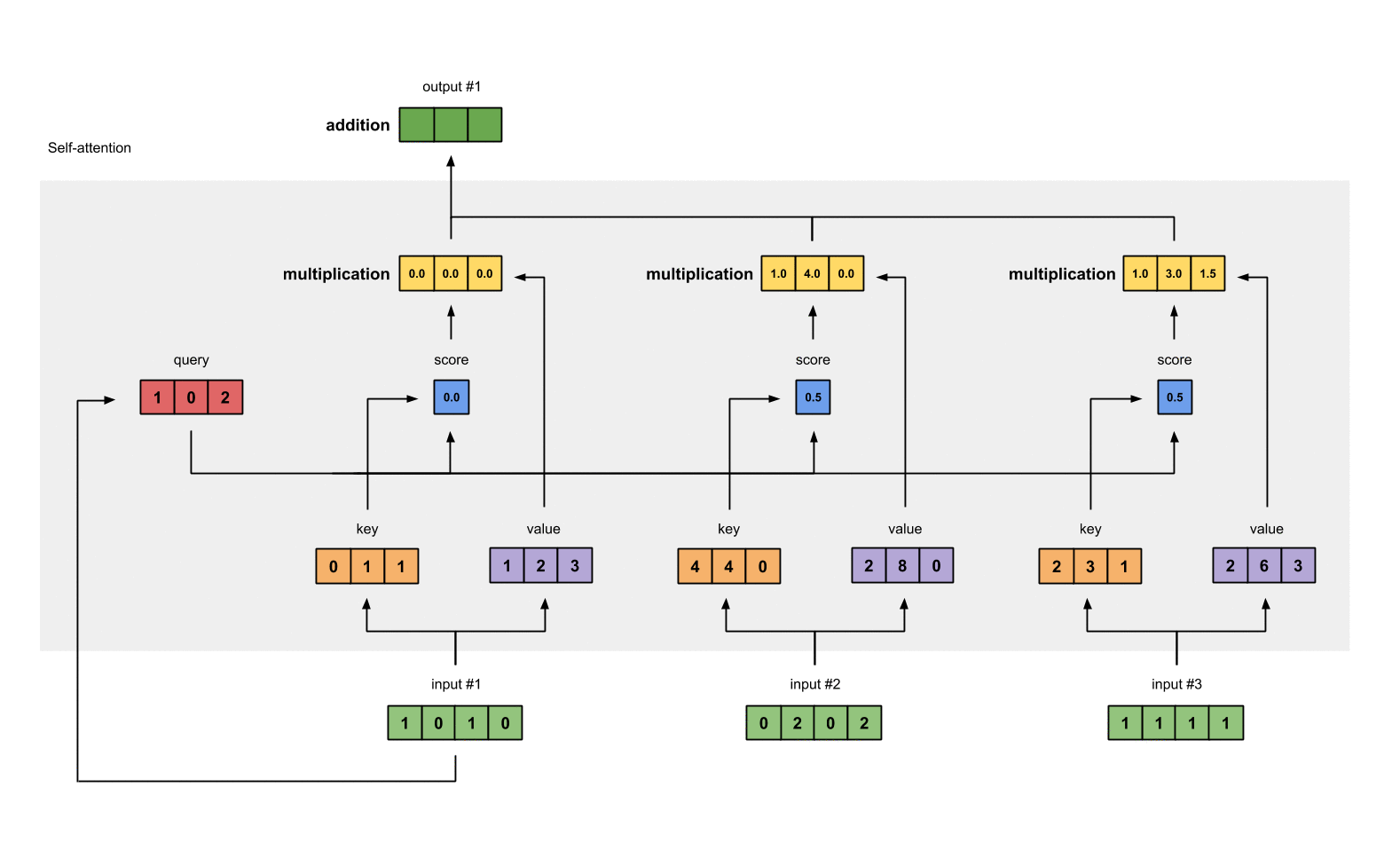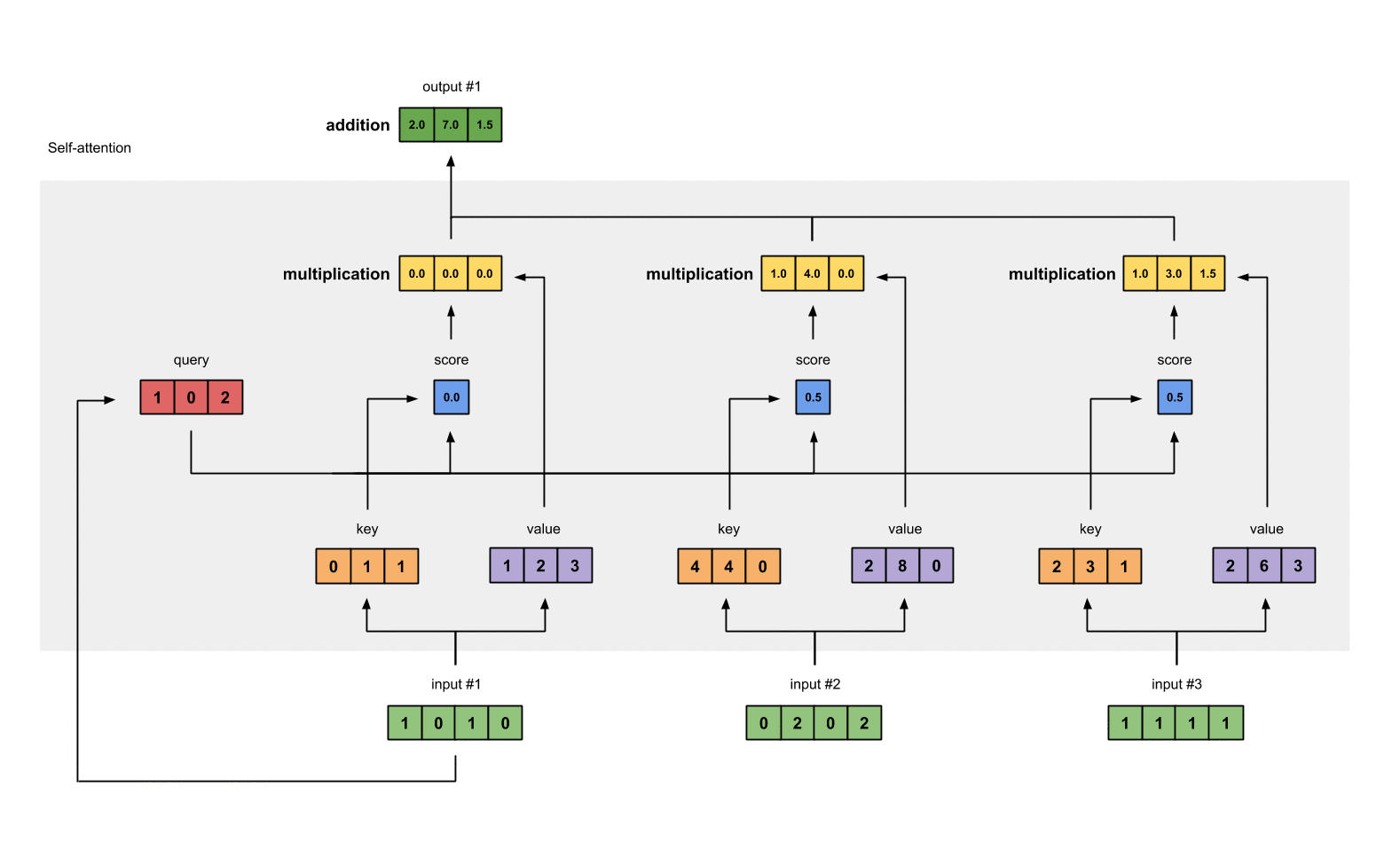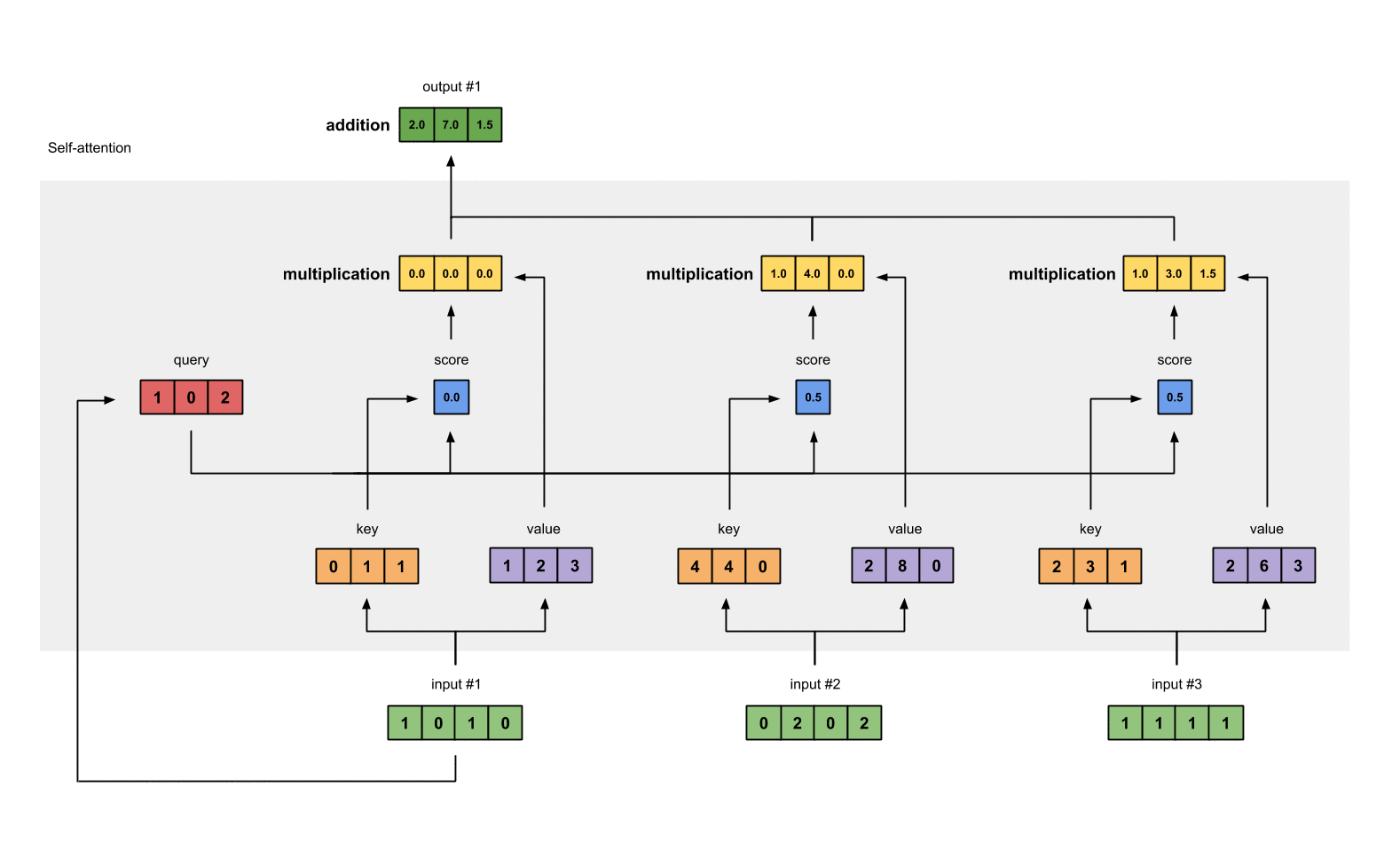
把所有的weighted values（黄色）进行element-wise的相加。

  [0.0, 0.0, 0.0]
+ [1.0, 4.0, 0.0]
+ [1.0, 3.0, 1.5]
-----------------
= [2.0, 7.0, 1.5]

得到结果向量[2.0, 7.0, 1.5]（深绿色）就是ouput1的和其他key交互的query representation。

第8步: 重复步骤4-7，获取output2，output3

现在，我们已经完成output1的全部计算，我们要对input2和input3也重复的完成步骤4～7的计算。

outputs = weighted_values.sum(dim=0)
print(outputs)

# tensor([[2.0000, 7.0000, 1.5000],  # Output 1
#         [2.0000, 8.0000, 0.0000],  # Output 2
#         [2.0000, 7.8000, 0.3000]]) # Output 3

tensor([[2.0000, 7.0000, 1.5000],
        [2.0000, 8.0000, 0.0000],
        [2.0000, 7.8000, 0.3000]])

福利: Tensorflow 2 实现

import tensorflow as tf

x = [
  [1, 0, 1, 0], # Input 1
  [0, 2, 0, 2], # Input 2
  [1, 1, 1, 1]  # Input 3
 ]

x = tf.convert_to_tensor(x, dtype=tf.float32)
print(x)

tf.Tensor(
[[1. 0. 1. 0.]
 [0. 2. 0. 2.]
 [1. 1. 1. 1.]], shape=(3, 4), dtype=float32)

w_key = [
  [0, 0, 1],
  [1, 1, 0],
  [0, 1, 0],
  [1, 1, 0]
]
w_query = [
  [1, 0, 1],
  [1, 0, 0],
  [0, 0, 1],
  [0, 1, 1]
]
w_value = [
  [0, 2, 0],
  [0, 3, 0],
  [1, 0, 3],
  [1, 1, 0]
]
w_key = tf.convert_to_tensor(w_key, dtype=tf.float32)
w_query = tf.convert_to_tensor(w_query, dtype=tf.float32)
w_value = tf.convert_to_tensor(w_value, dtype=tf.float32)
print("Weights for key: \n", w_key)
print("Weights for query: \n", w_query)
print("Weights for value: \n", w_value)

Weights for key: 
 tf.Tensor(
[[0. 0. 1.]
 [1. 1. 0.]
 [0. 1. 0.]
 [1. 1. 0.]], shape=(4, 3), dtype=float32)
Weights for query: 
 tf.Tensor(
[[1. 0. 1.]
 [1. 0. 0.]
 [0. 0. 1.]
 [0. 1. 1.]], shape=(4, 3), dtype=float32)
Weights for value: 
 tf.Tensor(
[[0. 2. 0.]
 [0. 3. 0.]
 [1. 0. 3.]
 [1. 1. 0.]], shape=(4, 3), dtype=float32)

keys = tf.matmul(x, w_key)
querys = tf.matmul(x, w_query)
values = tf.matmul(x, w_value)
print(keys)
print(querys)
print(values)

tf.Tensor(
[[0. 1. 1.]
 [4. 4. 0.]
 [2. 3. 1.]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[1. 0. 2.]
 [2. 2. 2.]
 [2. 1. 3.]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[1. 2. 3.]
 [2. 8. 0.]
 [2. 6. 3.]], shape=(3, 3), dtype=float32)

attn_scores = tf.matmul(querys, keys, transpose_b=True)
print(attn_scores)

tf.Tensor(
[[ 2.  4.  4.]
 [ 4. 16. 12.]
 [ 4. 12. 10.]], shape=(3, 3), dtype=float32)

attn_scores_softmax = tf.nn.softmax(attn_scores, axis=-1)
print(attn_scores_softmax)

# For readability, approximate the above as follows
attn_scores_softmax = [
  [0.0, 0.5, 0.5],
  [0.0, 1.0, 0.0],
  [0.0, 0.9, 0.1]
]
attn_scores_softmax = tf.convert_to_tensor(attn_scores_softmax)
print(attn_scores_softmax)

tf.Tensor(
[[6.3378938e-02 4.6831051e-01 4.6831051e-01]
 [6.0336647e-06 9.8200780e-01 1.7986100e-02]
 [2.9538720e-04 8.8053685e-01 1.1916770e-01]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[0.  0.5 0.5]
 [0.  1.  0. ]
 [0.  0.9 0.1]], shape=(3, 3), dtype=float32)

weighted_values = values[:,None] * tf.transpose(attn_scores_softmax)[:,:,None]
print(weighted_values)

tf.Tensor(
[[[0.  0.  0. ]
  [0.  0.  0. ]
  [0.  0.  0. ]]

 [[1.  4.  0. ]
  [2.  8.  0. ]
  [1.8 7.2 0. ]]

 [[1.  3.  1.5]
  [0.  0.  0. ]
  [0.2 0.6 0.3]]], shape=(3, 3, 3), dtype=float32)

outputs = tf.reduce_sum(weighted_values, axis=0)  # 6
print(outputs)

tf.Tensor(
[[2.        7.        1.5      ]
 [2.        8.        0.       ]
 [2.        7.7999997 0.3      ]], shape=(3, 3), dtype=float32)