cubic-bezier又称三次贝塞尔,主要是为animation生成速度曲线函数。
cubic-bezier(x1,y1,x2,y2)

此图中:
P0:(0,0) P1:(x1,y1) P2:(x2,y2) P3:(1,1)
(x1,x2 范围为 0-1) (y1,y2没规定,但是过大没必要也没意义。)
我对此曲线是这么理解的:假设P1,P2两个点为吸铁石,曲线是薄铁条(可以被吸铁石影响形状的那种)
那么这个曲线则是被 P1,P2两个吸铁石点拉扯形成的。
有一点需要注意,当这个点距离曲线越远,则拉扯力越大,曲线弧度越大。距离曲线越近,拉扯力越小,曲线弧度越小(这里和吸铁石相反。)
1 <!DOCTYPE html> 2 <html lang="zh-cn"> 3 <head> 4 <meta charset="UTF-8"> 5 <title>Document</title> 6 7 <style> 8 .animation { 9 width: 50px; 10 height: 50px; 11 background-color: #ed3; 12 -webkit-transition: all 2s cubic-bezier(.17, .86, .73, .14); 13 -o-transition: all 2s cubic-bezier(.17, .86, .73, .14); 14 transition: all 2s cubic-bezier(.17, .86, .73, .14); 15 } 16 .animation:hover { 17 -webkit-transform: translateX(400px); 18 -ms-transform: translateX(400px); 19 -o-transform: translateX(400px); 20 transform: translateX(400px); 21 } 22 </style> 23 </head> 24 <body> 25 <div class="animation"></div> 26 </body> 27 </html>
这段代码中 (x1=0.17 y1=0.86) (x2=0.73 y2=0.14) 可以画出此运动曲线为
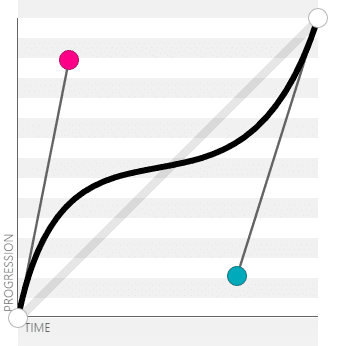
图片看不懂没关系,我教你,简单来讲可以把(0,0)当做物体的初始点,(0,1)当做物体的终点 注意这里不是(1,1),X轴从0到1为这个物体从初始点到终点的时间。
中间有段曲线大约在1/2路程的时候,发现随着时间的推移增加的很缓慢。那就说明这个物体在这段时间移动的慢。
好了,继续。下边有几个常用的曲线
ease: cubic-bezier(.25, .1, .25, 1);
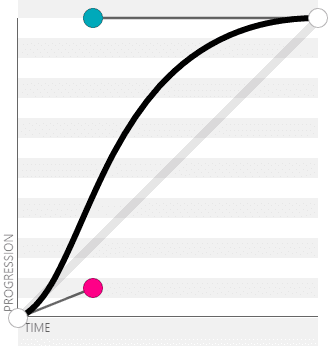
liner:cubic-bezier(0, 0, 1, 1) / cubic-bezier(1, 1, 0, 0)
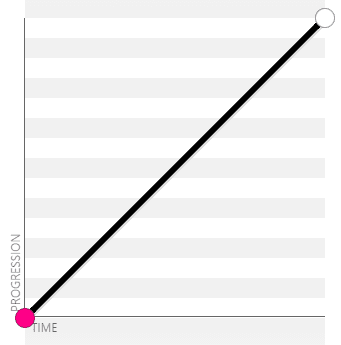
ease-in:cubic-bezier(.42, 0, 1, 1)
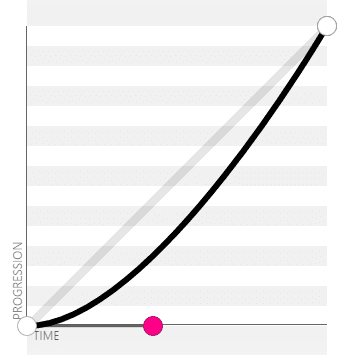
ease-out:cubic-bezier(0, 0, .58, 1)
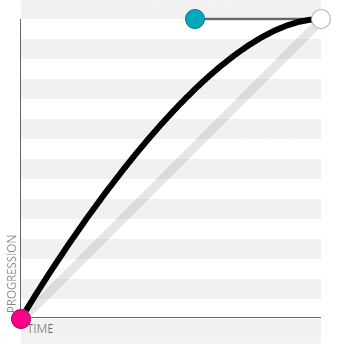
ease-in-out:cubic-bezier(.42, 0, .58, 1)
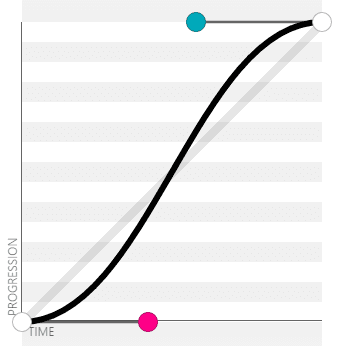
In Out . Back(来回的缓冲效果):cubic-bezier(0.68, -0.55, 0.27, 1.55)

参考:https://www.jianshu.com/p/d999f090d333
one more thing: 这个网址可以在线创作Cubic-bezier,蛮有意思的