A*算法（附c源码）

关于A*算法网上介绍的有很多，我只是看了之后对这个算法用c写了一下，并测试无误后上传以分享一下，欢迎指正！下面是我找的一个介绍，并主要根据这个实现的。

        寻路算法不止 A* 这一种, 还有递归, 非递归, 广度优先, 深度优先, 使用堆栈等等, 有兴趣的可以研究研究~~

简易地图

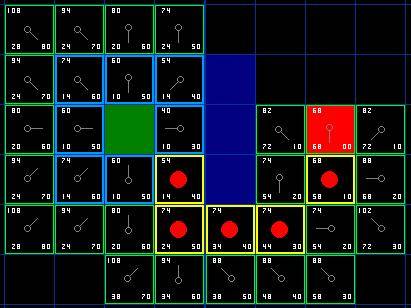
        如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.

        二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.

寻路步骤

        1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.

        2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.

        3. 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格

        图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.

        从 "开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式 F=G+H 来计算.

        F = G + H

                G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).

                H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 这里我们设定只可以上下左右移动).

        我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?

        从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:

        4. 把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.

        5. 检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.

        6. 如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.

        如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.

        然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.

        D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)

        就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...

        那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.

如何找回路径

        如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.

以上转自http://www.cnblogs.com/technology/archive/2011/05/26/2058842.html

下面是我的代码(c)：

一共三个文件：Apath.h 、Apath.c 、main.c 代码中有详细注释。

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>
 #include <stddef.h>
 #include <stdbool.h>

 #ifndef APATH_H
 #define APATH_H
 #endif

 #define TURE 1
 #define FAULT 0

 //约定：0是可走的，1表示障碍物不可走，2表示起点，3表示终点，4表示路径
 #define int_0 0
 #define int_1 1
 #define int_2 2
 #define int_3 3
 #define int_4 4

 #define MAP_MAX_X 10 //地图边界，二维数组大小
 #define MAP_MAX_Y 10

typedef struct LNode {
    int data;                   //对应数组中的数值
    int F;                      //F = G + H;
    int G;                      //G：从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径
    int H;                      //H：从指定的方格移动到终点 B 的估算成本
    int x, y;                   //对应数组中的坐标
    bool OPen_flag;             //在开放列表中为1，不在为0
    bool Close_flag;            //在关闭列表中为1，不在为0
    struct LNode* next;         //用于链表排序
    struct LNode* path_next;    //用于最终找到的路径
}LNode, *LinkList;

 LinkList InitList(); //返回一个初始化的链表
 LNode** malloc_array2D(int row, int col);
 void free_array2D(LNode **arr);
 LNode** Translate_array(int array[][10], int row, int col); //将一个普通数组翻译为单链表节点的数组
 void output(LNode **array, int row, int col);

 LNode* find_start_LNode(LNode** Arr, int row, int col); //从数组中找到始点
 LNode* find_end_LNode(LNode** Arr, int row, int col); //从数组中找到终点

 //忘记这些要干嘛了，重写吧
 //bool isExist_ALNode_in_List(LNode* curLNode, LinkList L_OpenList); //查看节点是否在链表中，在返回ture,不在返回fault
 //对关闭列表中的当前节点进行检查，看它周围的节点是否在OpenList链表里，不在:添加进去；在：检查经过它到达起点的G是否最小，是：修改，不是：不修改
 //LNode* check_CloseList_curLNode(LNode* curLNode, LNode* endLNode, LinkList L_OpenList, LinkList L_CloseList, LNode** Arr);

 LNode* pop_OpenList_minNode(LinkList L_OpenList); //返回开放列表中F值最小的节点
 void push_OpenList_Node(LinkList L, LNode *elem); //插入一个节点并排序
 bool insert_Into_CloseList(LNode* min_Open, LinkList L_CloseList);//插入OpenList中F值最小的节点到CloseList中去


 int count_LNode_G(LNode* curLNode, LNode* aheadLNode); //计算节点的G值
 int count_LNode_H(LNode* curLNode, LNode* endLNode); //计算节点的H值
 int count_LNode_F(LNode* curLNode); //计算节点的F值

 bool isExist_openList(LNode* curLNode); //查看节点是否在链表中，在返回ture,不在返回fault
 bool isExist_closeList(LNode* curLNode);
 bool isobstacle(LNode* curLNode);
 void check_around_curNode(LNode* cur, LNode* endLNode, LinkList open_list, LNode** Arr); //检查周围的节点，是否合适加入开放列表

#include "Apath.h"

LinkList InitList()
{
    LinkList L = (LinkList)malloc(sizeof(LNode));
    if (L == NULL)
    {
        printf("Defeat!");
        exit(1);
    }
    memset(L, 0, sizeof(LNode));

    return L;
}//LinkList()

LNode** malloc_array2D(int row, int col)
{
    LNode** map = (LNode**)malloc(row * sizeof(LNode*) + row * col * sizeof(LNode));
    LNode* head = (LNode*)(map + row);
    for (int i = 0; i < row; ++i)
        map[i] = head + i * col;

    return map;
}

LNode** Translate_array(int array[][10], int row, int col)
{
    LNode **map = malloc_array2D(10, 10);
    for (int i = 0; i < row; ++i)
        for (int j = 0; j < col; ++j)
        {
            (map[i] + j)->data = array[i][j];
            (map[i] + j)->G = 0;
            (map[i] + j)->H = 0;
            (map[i] + j)->F = 0; //(map[i] + j)->G + (map[i] + j)->H;
            (map[i] + j)->x = i;
            (map[i] + j)->y = j;
            (map[i] + j)->Close_flag = 0;
            (map[i] + j)->OPen_flag = 0;
            (map[i] + j)->next = NULL;
            (map[i] + j)->path_next = NULL;
        }
    return map;
}

void free_array2D(LNode **arr)
{
    free(arr);
}

//二维数组的访问必须指明位数，否则编译器不能解析
void output(LNode** array, int row, int col)
{
    //for (int i = 0; i < row; ++i)
    // for (int j = 0; j < col; ++j)
    // {
    // (array[i] + j)->F = j;
    // }
    for (int i = 0; i < row; ++i)
    {
        for (int j = 0; j < col; ++j)
        {
            printf("%d	", (array[i] + j)->data);
        }
        printf("
");
    }

    for (int i = 0; i < row; ++i)
    {
        for (int j = 0; j < col; ++j)
        {
            printf("(%d,%d),%d	", i, j, (array[i] + j)->data);
        }
        printf("
");
    }
}

//从数组中找到始点
LNode* find_start_LNode(LNode** Arr, int row, int col)
{
    LNode* start_LNode = NULL;
    for (int i = 0; i < row; ++i)
    {
        for (int j = 0; j < col; ++j)
        {
            if (2 == (Arr[i] + j)->data)
            {
                start_LNode = (Arr[i] + j);
                //起点H=0,G=0,F=0
                start_LNode->G = 0;
                start_LNode->H = 0;
                start_LNode->F = 0; //起点，则默认所有值为0
                return start_LNode; //返回节点
            }
        }
    }
    return NULL;
}

//从数组中找到终点
LNode* find_end_LNode(LNode** Arr, int row, int col)
{
    LNode* end_LNode = NULL;
    for (int i = 0; i < row; ++i)
    {
        for (int j = 0; j < col; ++j)
        {
            if (3 == (Arr[i] + j)->data)
            {
                end_LNode = (*(Arr + i) + j);
                end_LNode->F = 0;
                end_LNode->G = 0;
                end_LNode->H = 0;
                return end_LNode; //返回节点
            }
        }
    }
    return NULL;
}

//计算节点的G值
int count_LNode_G(LNode* curLNode, LNode* aheadLNode)
{
    if (curLNode->x == aheadLNode->x && curLNode->y == aheadLNode->y)
        return 0;

    if (aheadLNode->x - curLNode->x != 0 && aheadLNode->y - curLNode->y != 0)
        curLNode->G = aheadLNode->G + 14;
    else
        curLNode->G = aheadLNode->G + 10;
    return curLNode->G;
}

//计算节点的H值
int count_LNode_H(LNode* curLNode, LNode* endLNode)
{
    curLNode->H = abs(endLNode->x - curLNode->x) * 10 + abs(endLNode->y - curLNode->y) * 10;
    return curLNode->H;
}

//计算节点的F值
int count_LNode_F(LNode* curLNode)
{
    curLNode->F = curLNode->G + curLNode->H;
    return curLNode->F;
}

//按从小到大的顺序
void push_OpenList_Node(LinkList L, LNode *elem)
{
    LNode *p, *q;
    p = q = L;
    while (p->next != NULL && p->F < elem->F)
    {
        q = p;
        p = p->next;
    }

    if (p->F < elem->F)
        q = p;

    elem->next = q->next;
    q->next = elem;
    //插入成功，更改属性值OPen_flag = 1
    elem->OPen_flag = 1;
}

//返回开放列表中F值最小的节点
LNode* pop_OpenList_minNode(LinkList L_OpenList)
{
    LNode *elem = NULL;
    if (L_OpenList->next) //为了安全，防止访问空指针
    {
        L_OpenList->next->OPen_flag = 0;
        elem = L_OpenList->next;
        L_OpenList->next = L_OpenList->next->next;
        elem->next = NULL;
    }
    else
        printf("have a NULL point in pop_OpenList_mimNode()");
    return elem;
}

//插入OpenList中F值最小的节点到CloseList中去
bool insert_Into_CloseList(LNode* min_Open, LinkList L_CloseList)
{
    //对于CloseList中的节点并不需要排序,采用头插法
    min_Open->next = L_CloseList->next;
    L_CloseList->next = min_Open;
    min_Open->Close_flag = 1;
    return TURE;
}


bool isExist_openList(LNode* curLNode)
{
    return curLNode->OPen_flag;
}

bool isExist_closeList(LNode* curLNode)
{
    return curLNode->Close_flag;
}

bool isobstacle(LNode* curLNode)
{
    if (curLNode->data == 1)
        return TURE;
    else
        return FAULT;
}

//该节点是否可以加入开放列表
bool CanJoinOpenList(LNode* cur)
{
    if (cur->x > -1 && cur->y > -1) //边界检测
    {
        if (!isExist_closeList(cur) && !isobstacle(cur)) //既不在关闭列表里，也不是障碍物
        {
            return TURE;
        }
        else
            return FAULT;
    }
    return FAULT;
}

void insert_open(LNode *Node, LNode* ahead, LNode* endLNode, LinkList open_list, LNode** Arr)
{
    if (!CanJoinOpenList(Node))
        return;

    if (isExist_openList(Node))
    {
        //经由ahead节点，会不会使得F的值更小
        if (Node->x - ahead->x != 0 && Node->y - ahead->y != 0)
        {
            if (Node->F > (ahead->F + 14))
            {
                count_LNode_G(Node, ahead);
                count_LNode_F(Node); //H值没有改变，所以还是原来的值
                Node->path_next = ahead; //也不用再插入
            }
        }
        else
        {
            if (Node->F > (ahead->F + 10))
            {
                count_LNode_G(Node, ahead);
                count_LNode_F(Node); //H值没有改变，所以还是原来的值
                Node->path_next = ahead; //也不用再插入
            }
        }
    }
    else 
    {
        count_LNode_G(Node, ahead);
        count_LNode_H(Node, endLNode);
        count_LNode_F(Node);
        Node->path_next = ahead;
        push_OpenList_Node(open_list, Node);
    }
}

void check_around_curNode(LNode* cur, LNode* endLNode, LinkList open_list, LNode** Arr)
{
    const int x = cur->x;
    const int y = cur->y;

    //检查边界，画图标记下已经检查的节点
    if (y + 1 < MAP_MAX_Y)
    {
        insert_open(Arr[x] + y + 1, cur, endLNode, open_list, Arr);

        if (x + 1 < MAP_MAX_X)
            insert_open(Arr[x + 1] + y + 1, cur, endLNode, open_list, Arr);

        if(x - 1 >= 0)
            insert_open(Arr[x - 1] + y + 1, cur, endLNode, open_list, Arr);
    }

    if (x + 1 < MAP_MAX_X)
    {
        insert_open(Arr[x + 1] + y, cur, endLNode, open_list, Arr);

        if(y - 1 >= 0)
            insert_open(Arr[x + 1] + y - 1, cur, endLNode, open_list, Arr);
    }

    if (y - 1 >= 0)
    {
        insert_open(Arr[x] + y - 1, cur, endLNode, open_list, Arr);

        if (x - 1 >= 0)
            insert_open(Arr[x - 1] + y - 1, cur, endLNode, open_list, Arr);
    }

    if (x - 1 >= 0)
        insert_open(Arr[x - 1] + y, cur, endLNode, open_list, Arr);

    //insert_open(Arr[x] + y - 1, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x] + y + 1, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x + 1] + y, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x + 1] + y - 1, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x + 1] + y + 1, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x - 1] + y, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x - 1] + y + 1, cur, endLNode, open_list, Arr);
    //insert_open(Arr[x - 1] + y - 1, cur, endLNode, open_list, Arr);
}

 #include <stdio.h>
 #include "Apath.h"

 //为简单，干脆把把下面数组转为链表结构的数组
 //约定：0是可走的，1表示障碍物不可走，2表示起点，3表示终点，4表示路径
int array[10][10] = {
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 1, 3, 0, 0, 0 },
{ 0, 0, 2, 0, 0, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };

 int main()
 {
     int row = MAP_MAX_X, col = MAP_MAX_Y;
     printf("hello world!
");
     LNode **map = Translate_array(array, row, col); //这里将数组的地图转为节点map的地图
     output(map, 10, 10);

     LinkList open_List = InitList(); //定义并初始化一个开放列表
     LinkList close_List = InitList(); //一个封闭列表
     LNode* startLNode = find_start_LNode(map, row, col);
     LNode* endLNode = find_end_LNode(map, row, col);

     LNode* curLNode = startLNode; //当前节点=开始节点
     curLNode->G = 0; //计算节点的三个值

     count_LNode_H(curLNode, endLNode);
     count_LNode_F(curLNode);
     push_OpenList_Node(open_List, curLNode); //先将开始节点插入开放列表

     while (curLNode->data != 3)
     {
         //LNode *e = NULL;
         curLNode = pop_OpenList_minNode(open_List);
         insert_Into_CloseList(curLNode, close_List);
         //2、查看起点周围的点是否在开放列表里，不在加入，在检测经过该点F值是否最小等；
         check_around_curNode(curLNode, endLNode, open_List, map);
     }

     while (endLNode->path_next)
     {
         printf("x:%d---y:%d
", endLNode->path_next->x, endLNode->path_next->y);
         endLNode->path_next = endLNode->path_next->path_next;
     }

     free_array2D(map);
     return 0;
 }

测试结果（红线就是要找的路线）：