目录:
定义:
假设对象A具有指向它的对象T1 ... Tn。参数d是阻尼系数,取值范围在0和1之间,通常将d设置为0.85。C(A)被定义为从对象A出去的连接数。
对象A的PageRank计算公式如下:
PR(A)=(1−d)+d(PR(T1)/C(T1)+...+PR(Tn)/C(Tn))
当一个节点只有输出,没有输入的时候,因为d一般设置为0.85,所以:
PR(A)=(1-d)+ d *(0)= 0.15
计算原理:
每个对象的PR取决于指向它的对象的PR。在指向一个对象的所有对象都计算出了PR,才能够计算出该页面的PR值。
当所有对象形成闭环时,PR(A)可以使用简单的迭代算法计算,并且对应于web的规范化链接矩阵的主特征向量。
基本上,每次计算都会对各对象的最终值进行更接近的估计。通过对这些对象进行大量重复的计算,直到结果变化很小为止。
示例1:
每个页面都有一个输出链接(输出计数为1,即C(A)= 1,C(B)= 1)

假设A的PR(A)初始值为1
d = 0.85 //默认值
PR(A)=(1 - d)+ d(PR(B)/ 1)
PR(B)=(1 - d)+ d(PR(A)/ 1)
//即
PR(A)= 0.15 + 0.85 * 1 = 1
PR(B)= 0.15 + 0.85 * 1 = 1
假设A的PR(A)初始值为0
PR(A)= 0.15 + 0.85 * 0 = 0.15
PR(B)= 0.15 + 0.85 * 0.15 = 0.2775
//完成一次迭代,继续第二次迭代
PR(A)= 0.15 + 0.85 * 0.2775 = 0.385875
PR(B)= 0.15 + 0.85 * 0.385875 = 0.47799375
//第三次迭代
PR(A)= 0.15 + 0.85 * 0.47799375 = 0.5562946875
PR(B)= 0.15 + 0.85 * 0.5562946875 = 0.622850484375
//结果数值不断上升,但当达到1.0时,停止增加。
假设A的PR(A)初始值为40,B的PR(B)初始值为40
//初始值
PR(A)= 40
PR(B)= 40
//第一次迭代
PR(A)= 0.15 + 0.85 * 40 = 34.25
PR(B)= 0.15 + 0.85 * 0.385875 = 29.1775
//第二次迭代
PR(A)= 0.15 + 0.85 * 29.1775 = 24.950875
PR(B)= 0.15 + 0.85 * 24.950875 = 21.35824375
//结果数值不断下降,但当达到1.0时,停止下降。
性质:
当没有节点只进不出时,PageRank计算结果符合“ 归一化概率分布 ”,所有节点的PageRank平均值为1.0。
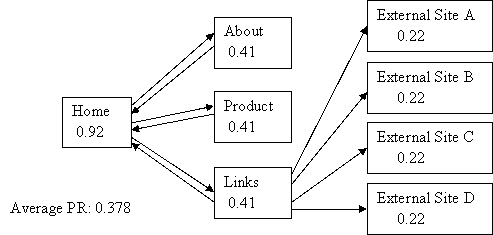
示例2:

该实例不满足只进不出条件,第三列的节点只有输入,没有输出,所以PR的平均值不等于1.0
参考资料:
http://www.cs.princeton.edu/~chazelle/courses/BIB/pagerank.htm