图像的几何变换是指改变图像的几何位置、几何形状、几何尺寸等几何特征。
一.图像的平移
图像平移是将一幅图像中所有的点都按照指定的平移量在水平、垂直方向移动,平移后的图像与原图像相同。
利用齐次坐标,变换前后图像上的点P0(x0,y0)和P(x,y)之间的关系可以用如下的矩阵变换表示为

平移变换的几点说明:
①平移后图像上的每一点都可以在原图像中找到对应的点。对于不在原图像中的点,可以直接将它的像素值统一设置为0或这255(对于灰度图就是黑色或者白色);
②若图像平移后并没被放大,说明移出的部分被截断,原图像中有像素点被移出显示区域。
③若不想丢失被移出的部分图像,则将新生成的图像扩大。
代码如下:
clear all;
close all;
I = imread('lenna.jpg');
delta_x = 10; % 水平方向的偏移量
delta_y = 10; % 垂直方向的偏移量
[M N] = size(I); % 原图像的宽度和高度
I2 = zeros(M, N);
for x = 1 : M
if x + delta_x <= M
for y = 1 : N
if y + delta_y <= N
I2(x + delta_x, y + delta_y) = I(x, y);
end
end
end
end
subplot(1, 2, 1), imshow(I);
subplot(1, 2, 2), imshow(uint8(I2));
平移后的图像显示如下:

二.图像的旋转
一般图像的旋转是以图像的中心为原点,旋转一定的角度,即将图像上的所有像素都旋转一个相同的角度。
图像的旋转变换也可以用矩阵变换表示。设点P0(x0, y0)旋转θ角后的对应点为P(x, y),则变换公式为:
 或者是
或者是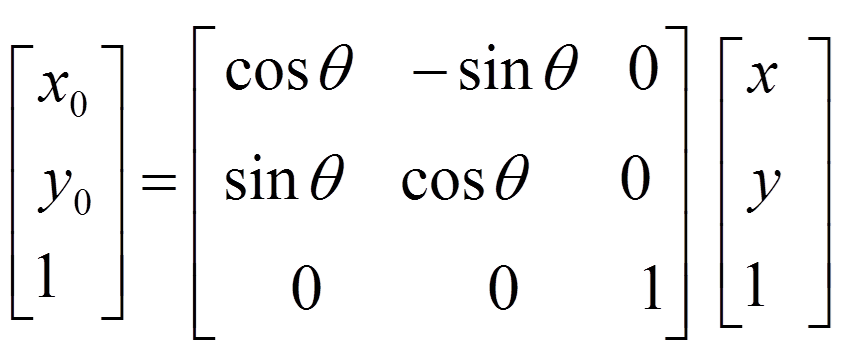
利用公式进行图像旋转变换时,需要注意如下两点:
①为了避免图像信息的丢失,图像旋转后必须进行平移变换。
②图像旋转之后,会出现许多空洞点,我们必须对这些空洞点进行填充处理,否则图像旋转后的效果不好,一般也将这种操作称作为插值处理。
上述的旋转是绕坐标轴原点(0,0)进行的,如果是绕某一个指定点旋转,则先要将坐标系平移到该点,再进行旋转,然后将旋转后的图像平移回原坐标系。因此,我们得到绕任一点(x0,y0)的旋转变换公式为:
x’ = (x-x0)·cos(θ) + (y-y0)·sin(θ) + x0
y’ = -(x-x0)·sin(θ) + (y-y0)·cos(θ) + y0
代码如下:
clear all;
close all;
I = imread('lenna.jpg');
H = 1; % 矩阵pix第一个元素,即高度
W = 2; % 矩阵pix第二个元素,即宽度
[M N] = size(I); % M为原图像的高度,N为原图像的宽度
theta = 30 / 180 * pi; % 旋转角度为顺时针方向30度
rot = [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1]; % 变换矩阵
inv_rot = inv(rot); % 变换矩阵的逆运算
pix1 = [1 1 1] * rot; % 变换后图像左上点的坐标
pix2 = [1 N 1] * rot; % 变换后图像右上点的坐标
pix3 = [M 1 1] * rot; % 变换后图像左下点的坐标
pix4 = [M N 1] * rot; % 变换后图像右下点的坐标
height = round(max([abs(pix1(H) - pix4(H)) abs(pix2(H) - pix3(H))]) + 0.5); % 变换后图像的高度
width = round(max([abs(pix1(W) - pix4(W)) abs(pix2(W) - pix3(W))]) + 0.5); % 变换后图像的宽度
delta_y = abs(min([pix1(H) pix2(H) pix3(H) pix4(H)])); % y方向负轴超出的偏移量
delta_x = abs(min([pix1(W) pix2(W) pix3(W) pix4(W)])); % y方向负轴超出的偏移量
I2 = zeros(height, width);
for y = 1 - delta_y : height - delta_y
for x = 1 - delta_x : width - delta_x
pix = [y x 1] * inv_rot;
if pix(H) > 0.5 && pix(W) > 0.5 && pix(H) < M && pix(W) < N
I2(y + delta_y, x + delta_x) = I(round(pix(H)), round(pix(W)));
end
end
end
subplot(1, 2, 1), imshow(I), title('原图像');
subplot(1, 2, 2), imshow(uint8(I2)), title('旋转后的图像');
旋转后的图像显示如下:

三.图像的比例缩放
图像的比例缩放变换是指给定的图像在x轴方向按比例缩放fx倍,在y轴方向缩放fy倍,从而获得一幅新的图象。比例缩放前后两点P0(x0,y0)、P(x,y)之间的关系用矩阵形式可以表现为:
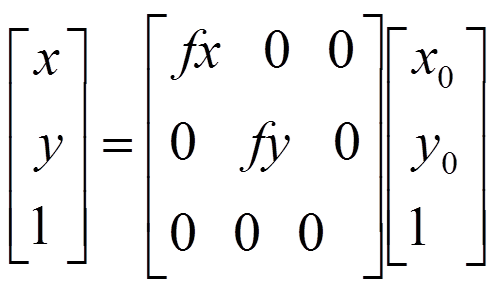
在图像放大的正变换中,会出现很多的空格。因此,需要对放大后所多出来的空格填入适当的像素值。一般采用最邻近插值和线性插值法。
图像缩小代码如下:
clear all;
close all;
I = imread('lenna.jpg');
[M N] = size(I);
width = int32(0.5 * N) % 将图像宽度缩小为原来的1/2
height = int32(0.5 * M) % 将图像高度缩小为原来的1/2
I2 = uint8(zeros(height, width));
widthScale = floor(N / width);
heightScale = floor(M / height);
for y = 1 : height
for x = 1 : width
oldX = x * widthScale;
oldY = y * heightScale;
I2(y, x) = I(oldY, oldX);
end
end
a1 = subplot(1, 2, 1);
imshow(I), title('原图像');
a2 = subplot(1, 2, 2);
imshow(I2), title('缩小后的图像');
set(a2, 'XLim', get(a1, 'XLim'), 'YLim', get(a1, 'YLim')); % 将两个sunplot的x,y轴单位长度设为一样
缩小后的图像显示如下:

图像放大代码如下:
clear all;
close all;
I = imread('lenna.jpg');
[M N] = size(I);
width = 2 * N; % 将图像宽度放大为原来的2倍
height = 2 * M; % 将图像高度放大为原来的2倍
I2 = uint8(zeros(height, width));
widthScale = width / N;
heightScale = height / M;
for y = 1 : height
for x = 1 : width
oldX = round(x / widthScale);
oldY = round(y / heightScale);
if oldX == 0 oldX = 1; end
if oldY == 0 oldY = 1; end
if oldX > N oldX = N; end
if oldY > M oldY = M; end
I2(y, x) = I(oldY, oldX);
end
end
a1 = subplot(1, 2, 1);
imshow(I), title('原图像');
a2 = subplot(1, 2, 2);
imshow(I2), title('放大后的图像');
set(a1, 'XLim', get(a2, 'XLim'), 'YLim', get(a2, 'YLim')); % 将两个sunplot的x,y轴单位长度设为一样
放大后的图像显示如下:
