problem:

In a program that uses Opencv for image processing. My goal is to use the camera to identify the precise coordinates of multiple balls. But because of the light, in the identification process, the coordinates of the ball sometimes accurate sometimes sometimes inaccurate, in order to make each identified the ball coordinates can be more accurate. We need to each ball to identify the coordinates of the average to get a more accurate coordinates.
I use the following way to average the ball coordinates.
First, we should save the coordinates identified this time to the array ballpre [], and then to the next time to identify the ball in the process, with the coordinates (x, y) and ballpre [] coordinates in the calculation of the distance. The minimum distance is to identify the coordinates of a same small ball, and then add them together. Finally using the sum of coordinates divided by the number of times identified by the coordinates.
At first I thought that my method was right, but at the time of the run, I found that the result was wrong.
Why this error impress I most?
Because this problem I spent a lot of time, at first thought that the algorithm error, and constantly to check the algorithm and grammar. There is another reason that this project is submitted in my first time to participate in the competition.
How did I find it? What is the error?
And then I print out the data every time, analyze it, I found that the reason is that some of the ball in a recognition process has not been identified, so it is divided by the number of identification should not be the total number of identification.
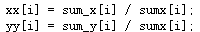
Solution:Add an array to control the number of times the ball is recognized. We use the elements in this array as the denominator of the above formula.
The following is the specific code:
for (int i = 0; i < MIN(count_x, 20); i++)
{
if (ci == 0)
{
xx1[i] = x[i];
yy1[i] = y[i];
sum_x[i] += x[i];
sum_y[i] += y[i];
for (int i = 0; i < count_x; i++)
{
sumx[i] = 1;
}
for (int i = count_x; i < 100; i++)
{
sumx[i] = 0;
}
}
for (int j = 0; j < count_x; j++)
{
//float * q = (float *)cvGetSeqElem(cir, j);
if (ci > 0)
{
double a = pow(x[j] - xx1[i], 2) + pow(y[j] - yy1[i], 2);
if (cvRound(sqrt(a)) <= 15)
{
//cout << cvRound(q[0]) << " " << x1[i] << endl;
//cout << cvRound(q[1]) << " " << y1[i] << endl;
//cout << "sqrt(a)" << sqrt(a) << endl;
sum_x[i] += x[j];
sum_y[i] += y[j];
sumx[i]++;
break;
}
if (j == count_x&&cvRound(sqrt(a)) > 15)
{
sum_x[j] += x[j];
sum_y[j] += y[j];
sumx[j]++;
}
}
}
xx[i] = sum_x[i] / sumx[i];
yy[i] = sum_y[i] / sumx[i];
}
}