计算几何中计算三角形面积
在计算几何里,我们知道,△ABC的面积就是“向量AB”和“向量AC”两个向量叉积的绝对值的一半。其正负表示三角形顶点是在右手系还是左手系。

所以得到三角形面积

特别注意:
以上得到是有向面积(有正负)!
凸多边形的三角形剖分
很自然地,我们会想到以 P1为扇面中心,连接P1Pi就得到N-2个三角形,由于凸性,保证这些三角形全在多边形内,那么,这个凸多边形的有向面积:A=sigma(Ai) (i=1…N-2)
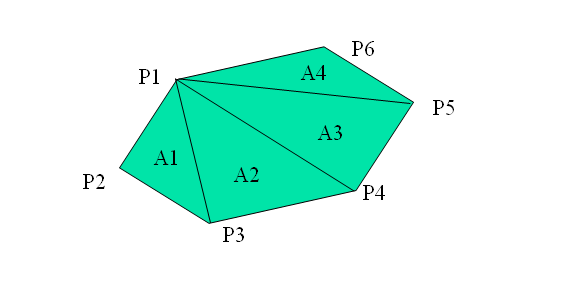
凹多边形的面积
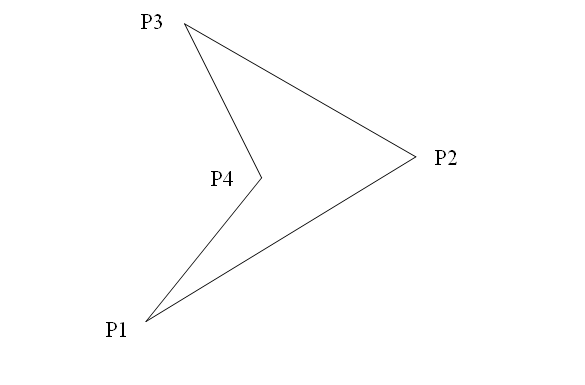
多边形面积公式:A=sigma(Ai) (i=1…N-2)
结论:
“有向面积”A比“面积”S其实更本质!
任意点为扇心的三角形剖分:
我们能把多边形分成N-2个三角形,为什么不能分成N个三角形呢?
比如,以多边形内部的一个点为扇心,就可以把多边形剖分成 N个三角形。

前面的三角剖分显然对于多边形内部任意一点都是合适的!
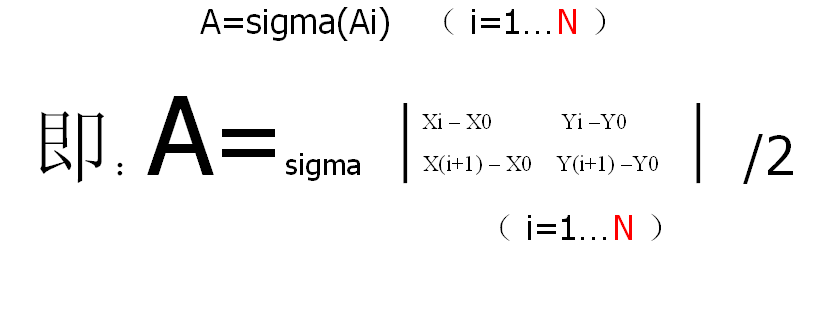
能否把扇心移到多边形以外呢?
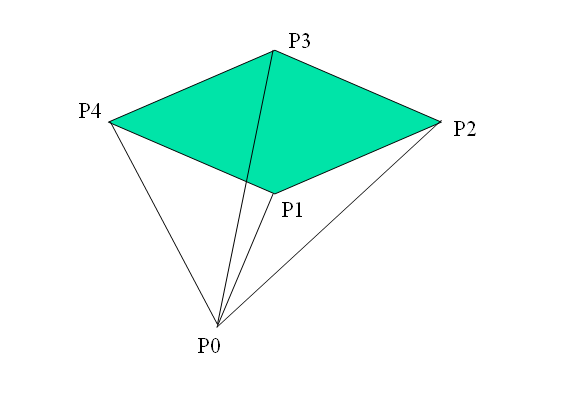
既然内外都可以,为什么不设P0为坐标原点呢?
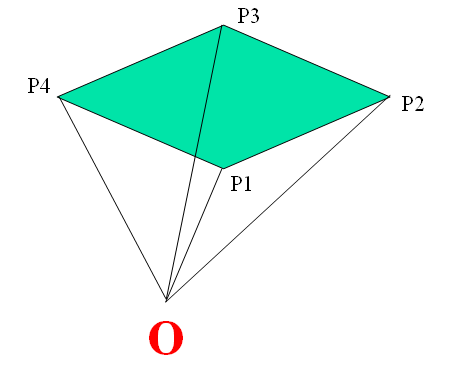
最终简化公式(包括凹多边形):

---------------------
作者:相思明月楼
来源:CSDN
原文:https://blog.csdn.net/Adusts/article/details/80546770
版权声明:本文为博主原创文章,转载请附上博文链接!