本期的学习来源是:https://www.bilibili.com/video/BV1Y7411d7Ys?p=6
代码来源:https://blog.csdn.net/bit452/article/details/109680909
搞了两天的智能家居,换了一堆的面板开关,顺便学了一些电工的知识,终于有时间开始继续学习Pytorch了
逻辑斯蒂回归
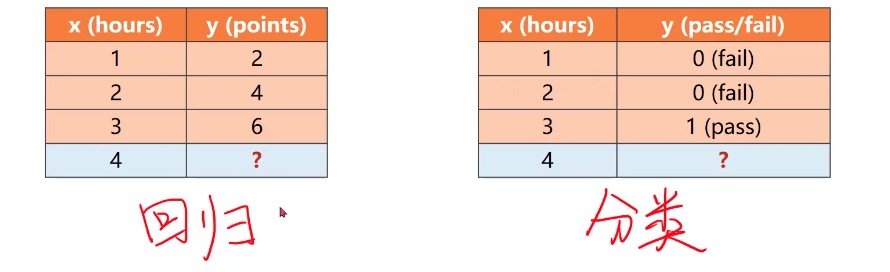
名为逻辑斯蒂回归,但实际上是分类
分类问题中输出的是概率,而不是单独列出一个结果,对比上图可知
torchvision是Pytorch的常用工具包,datasets里面有常用的数据集
logistic函数:
由输出值映射到[0,1]的概率分布上
其函数图为
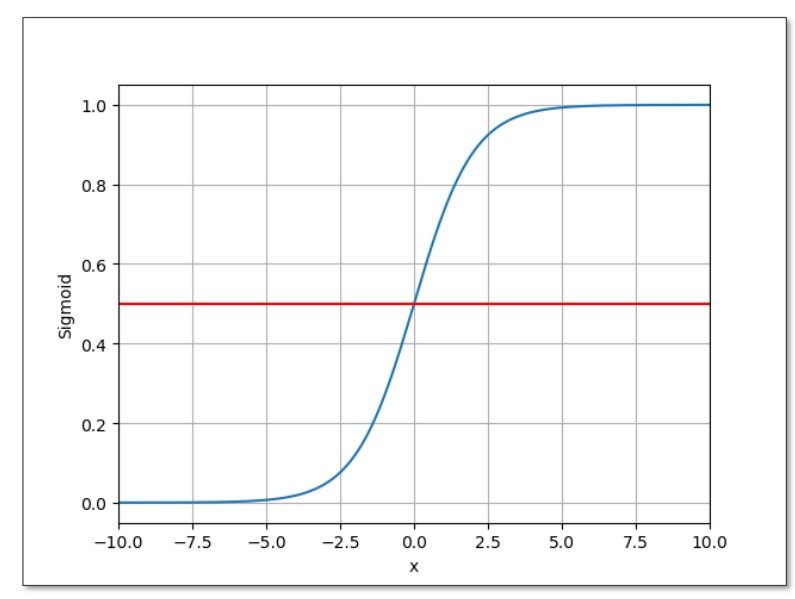
可以观察到当x->0的时候,其结果等于0.5
饱和函数:在超过一定值时,其导数绝对值趋近于零(逐渐变得平缓
而我们要做的是将Y_hat的值导入到logistic函数的x中,输出的结果便是概率
sigmoid函数:映射到[-1,1]之间,同样也是饱和函数
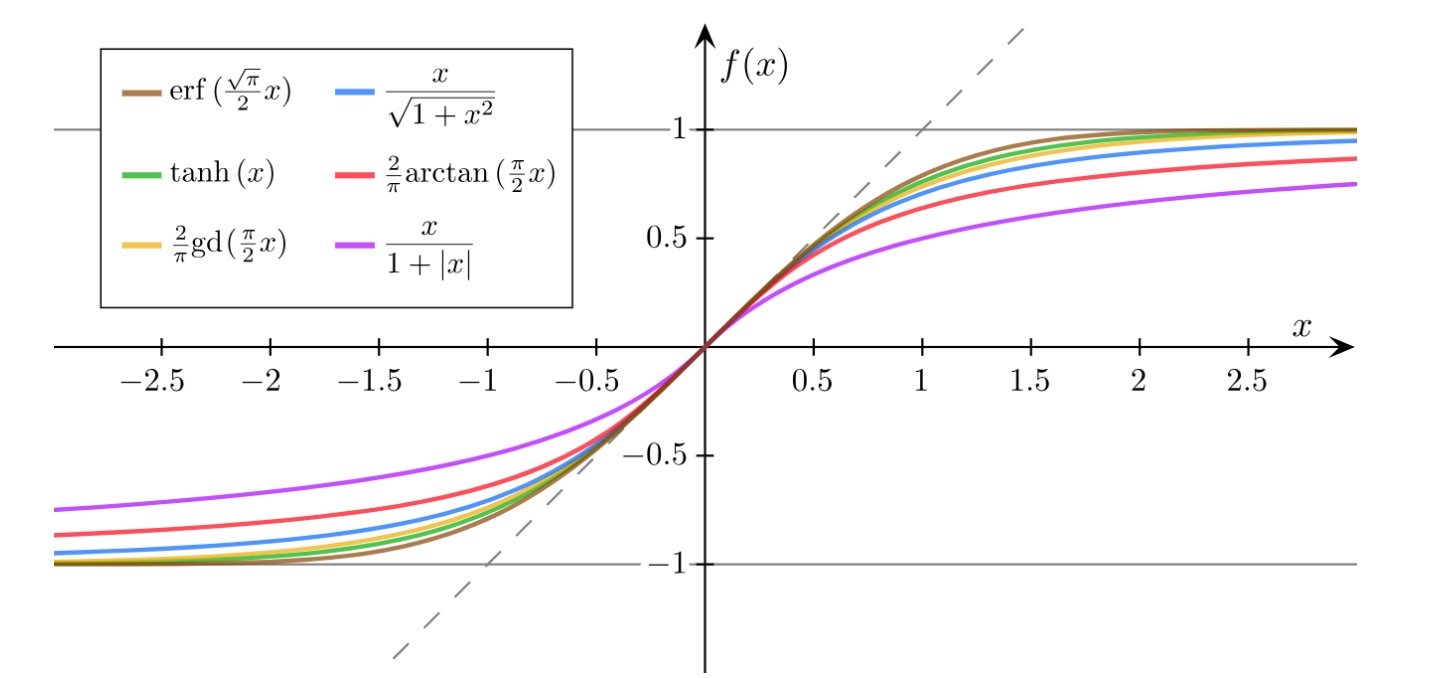
logistic函数是sigmoid函数的典型
西格玛这个符号在深度学习里面,常常意为sigmoid函数
作用:比较的是两个分布之间的差异
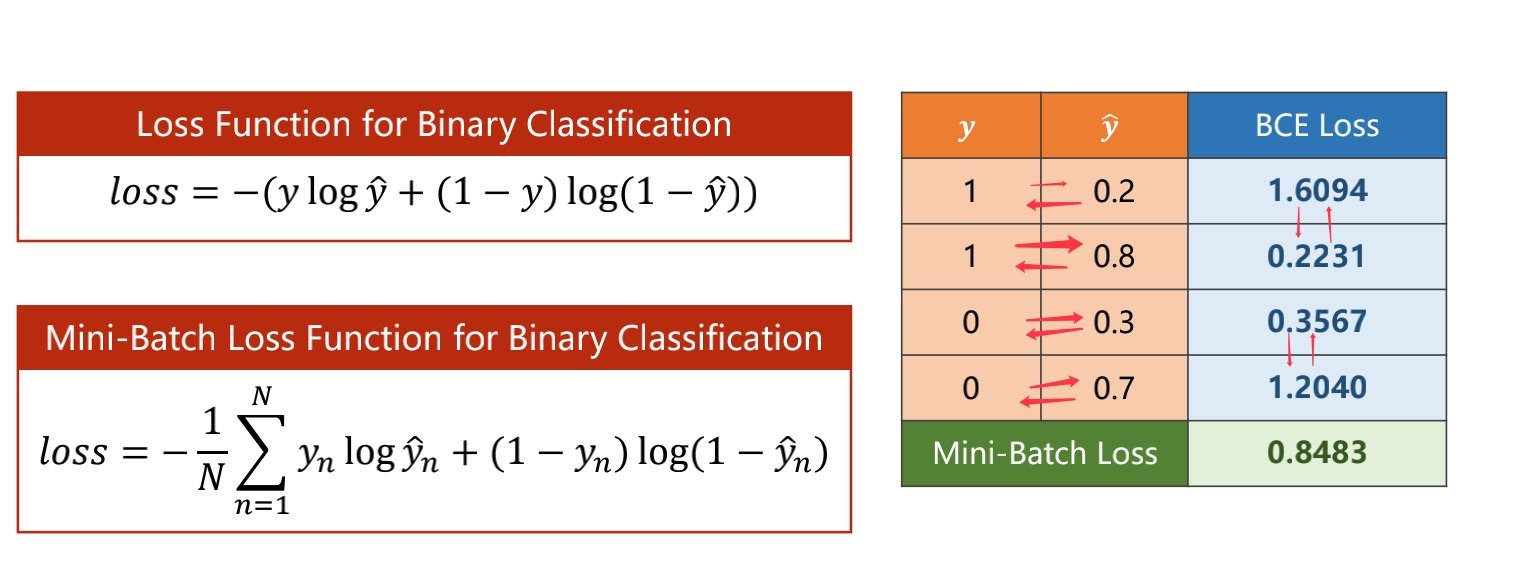
对比箭头两边,可以看到,当我们所得的预测值与标签值越接近,则我们的损失函数会越小
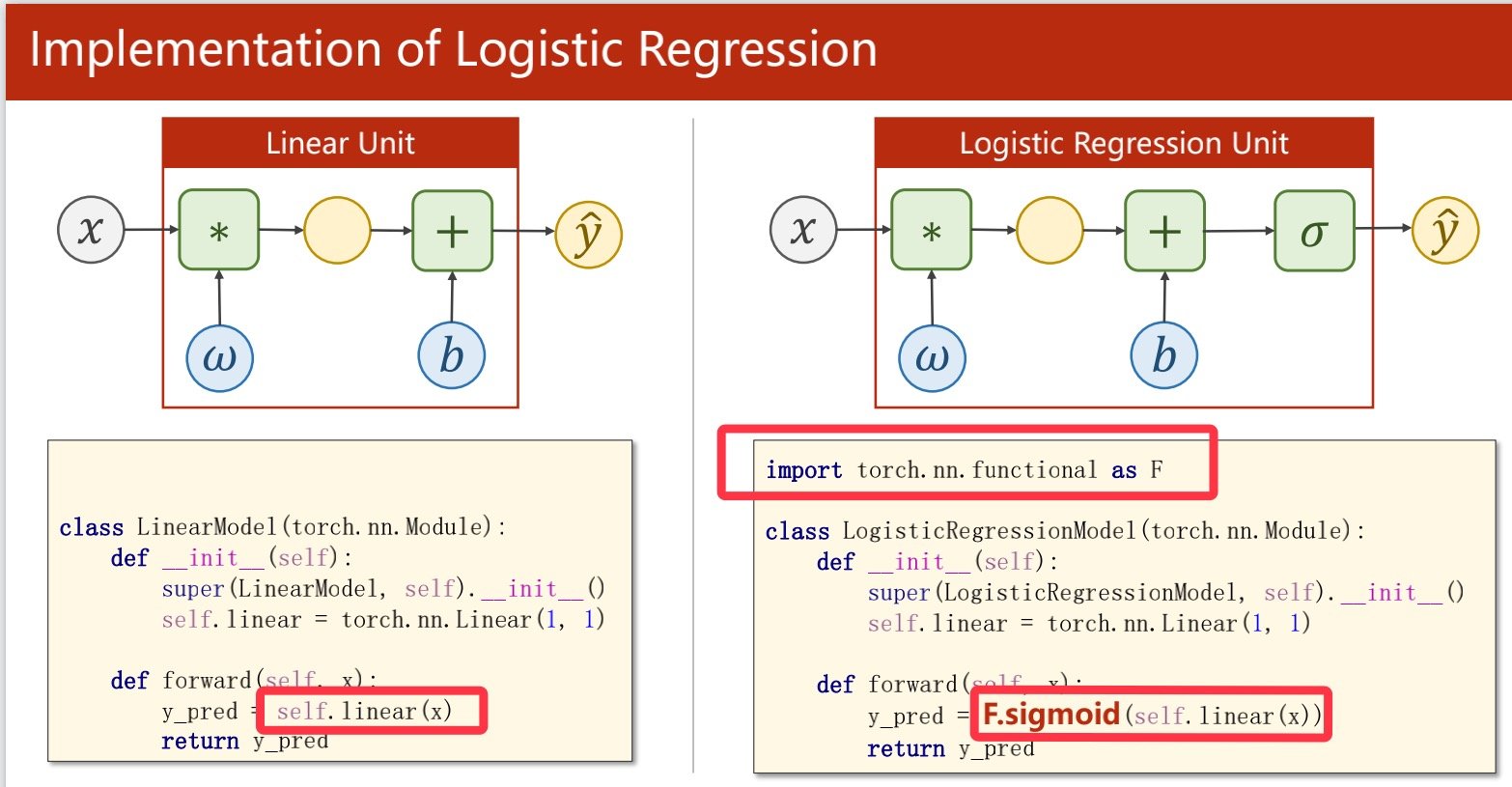
比以往的线性模型计算多了一步sigmoid函数
会影响到我们对学习率的更新
相比以前的线性函数有两个差别,一在数据准备上要先分好类,二在sigmoid函数
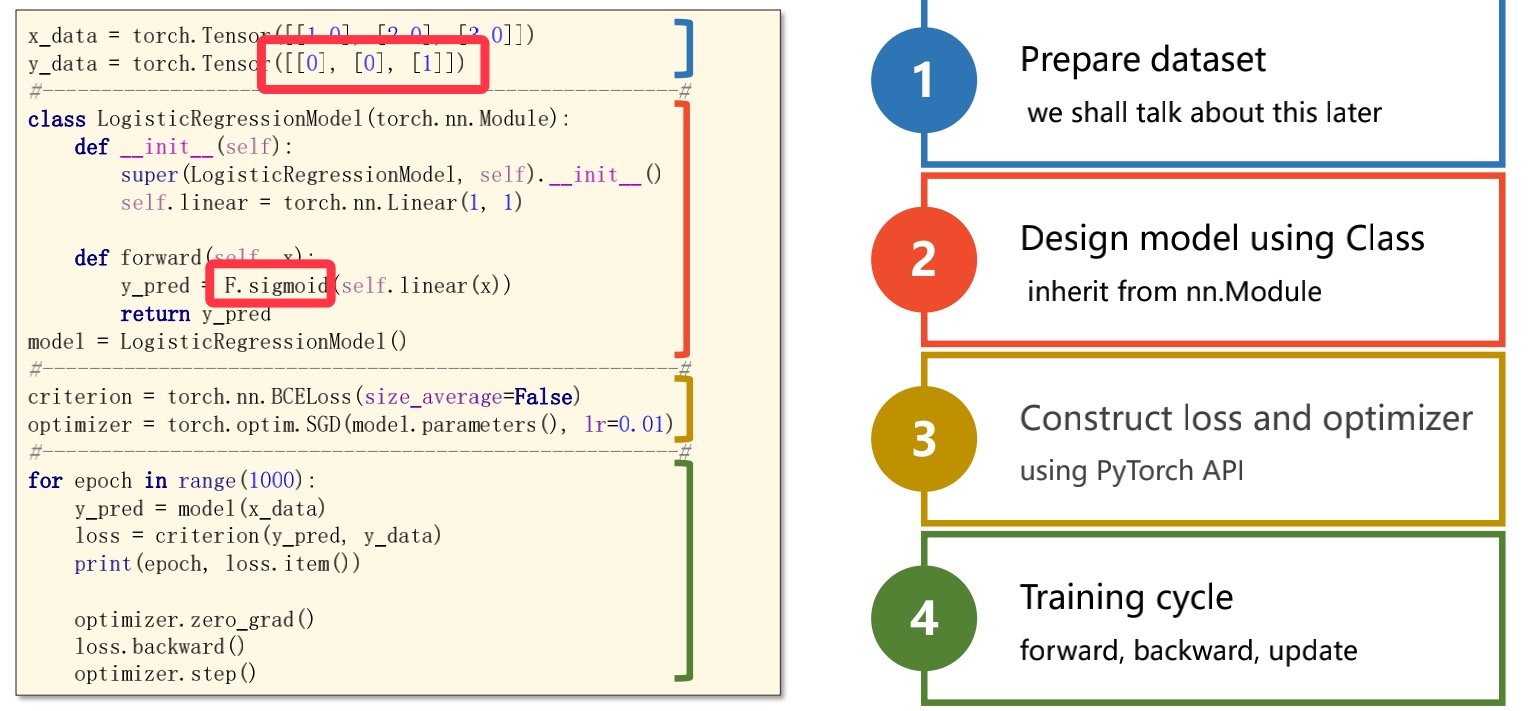
代码例子:
import torch
# import torch.nn.functional as F
# prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
# 和之前的数据集不同,此时将是否通过考试设置为1和0
y_data = torch.Tensor([[0], [0], [1]])
#design model using class
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self, x):
# y_pred = F.sigmoid(self.linear(x))
y_pred = torch.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
# construct loss and optimizer
# 默认情况下,loss会基于element平均,如果size_average=False的话,loss会被累加。
criterion = torch.nn.BCELoss(size_average = False)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
# training cycle forward, backward, update
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
最后得到的结果是
w = 1.2258338928222656
b = -2.9603376388549805
y_pred = tensor([[0.8747]])
此时的w*x-b得到的结果是指通过考试的概率,可以从中得到,当x=4的时候,通过的概率为0.8747,而不是之前的,x=4会有可能得到8分
多维特征输入
在pytorch中术语为特征,而在数据库中被称为字段,每行为一个样本
下图中以8维特征为例
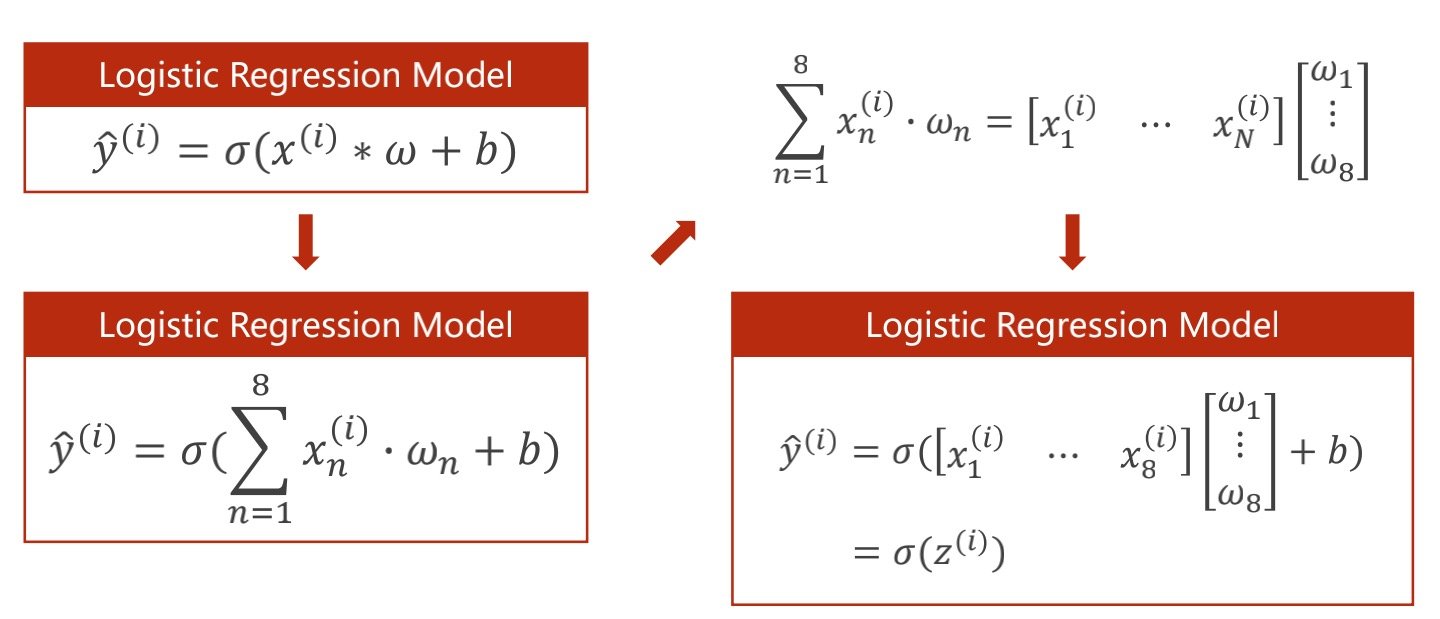
为了更好表示,合并为矩阵运算
原本单个样本是1*8和8*1的矩阵相乘得到结果,现在换成矩阵运算,可以得到多行一列的矩阵
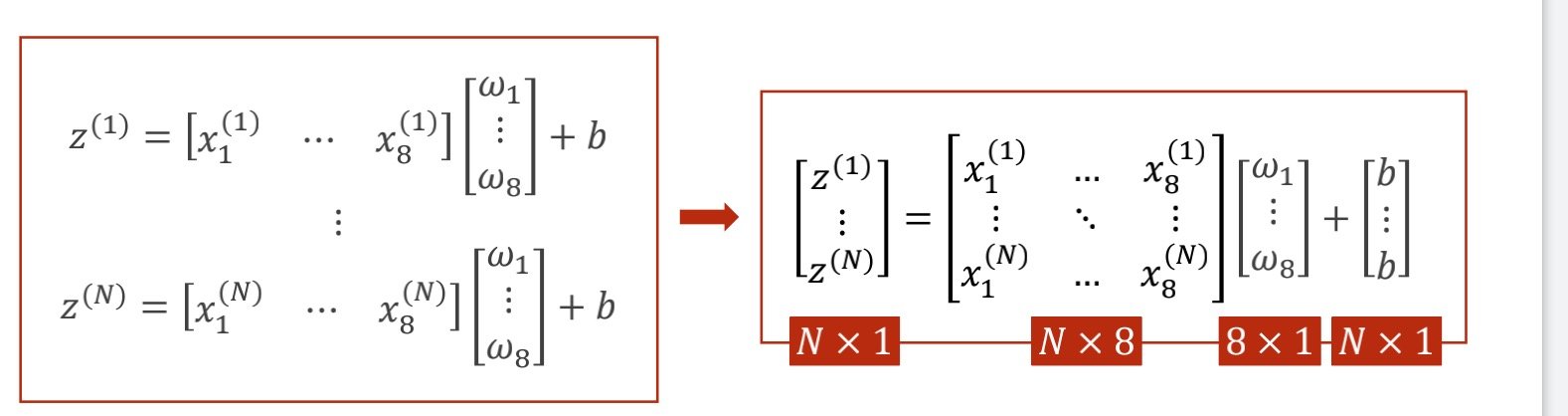
在代码中的线性模型做以下修改

linear(8,1)表示的是输入的维度为8(特征数),输出的维度为1(单个标量,可以直接表示概率
当得到输出维度为2的时候,得不到单个的标量
此时可以使用linear(2,1),巧妙转化为1维的标量
对矩阵变换的理解:是空间维度的变换/映射,转换数据信息的维度
将多个线性linear,可以实现维度分布式降低(例如8->6->4->2->1)
为什么要多层降维呢?
因为直接8维降1维中间的神经元少,学习效果可能不佳,所以要多几层,但是也不能太多,否则会造成过拟合
目的是为了找到更好的特征
给线性变换加上非线性变化的因子(sigmoid函数,见上
泛化与拟合
泛化是指普遍的适应性(即为抓住问题的本质,获取样本中的真实信息)
而过拟合是指将样本中的噪声也同时学入(类似于死记硬背
数据的读取
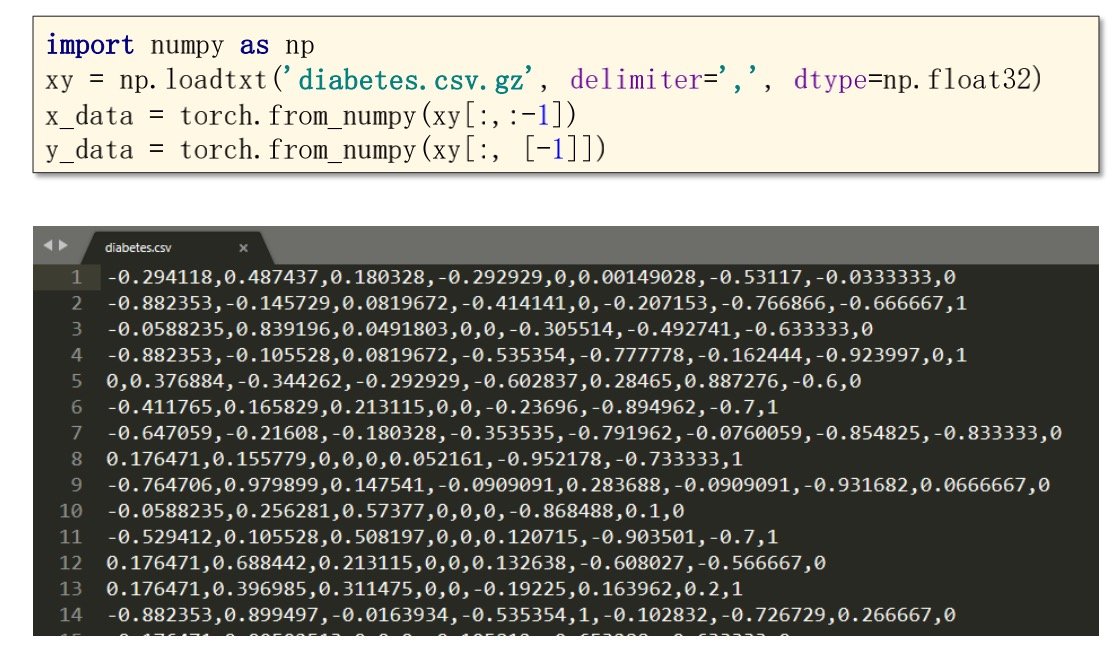
读取Y_data的时候,-1列要加上中括号才能形成矩阵,否则得到的会是列向量(其实转置一下也可以
激活函数
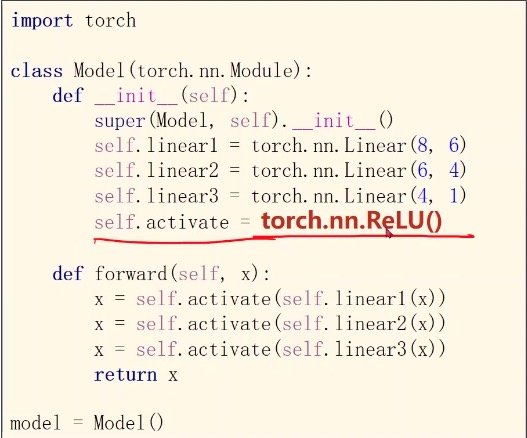
在__init__中进行修改
神经网络中常使用relu(),会将多维映射到[0,1]之间,并且在低于0时直接输出0