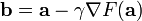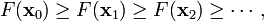从wiki上面摘录下来
http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95
这个方法的作用是, 通过迭代, 迅速取得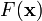
的最小值所在的坐标, 这样就可以作为一些惩罚函数的优化方法
梯度下降法，基于这样的观察：如果实值函数 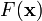在点 
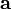处可微且有定义，那么函数 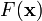在 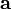点沿着梯度相反的方向 
下降最快。
因而，如果
对于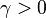 
为一个够小数值时成立，那么 
。
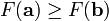考虑到这一点，我们可以从函数 
的局部极小值的初始估计 
出发，并考虑如下序列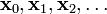 
使得
因此可得到
如果顺利的话序列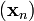 
收敛到期望的极值。注意每次迭代步长 
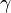可以改变。
下侧的图片示例了这一过程，这里假设 定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线(水平集)，即函数 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数 值最小的点。
之所以学到这个算法, 是因为模式识别中的感知器算法, 应用了这个方法去获得最快收敛到最小值的惩罚函数