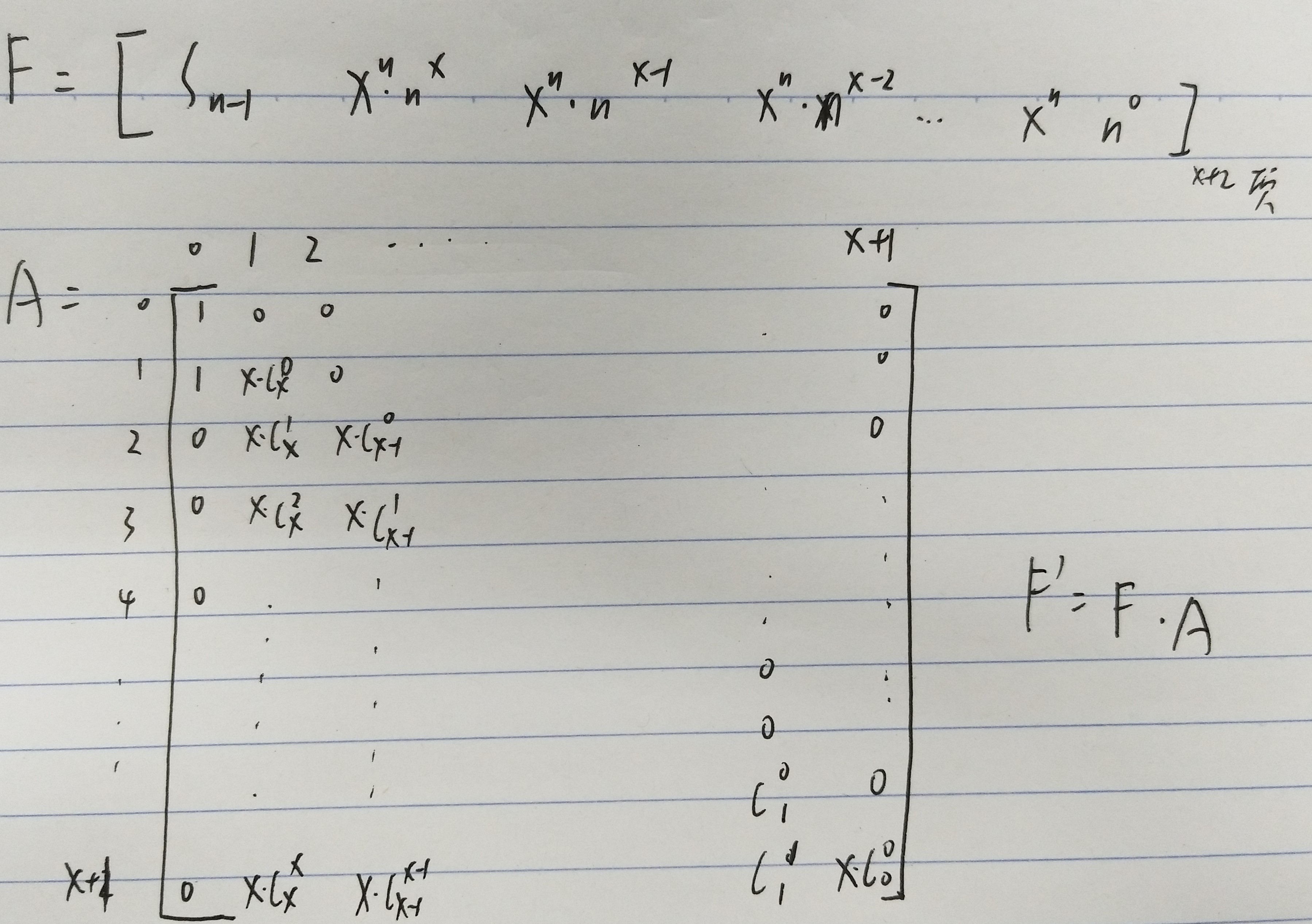hdu3483 A Very Simple Problem 非线性递推方程2 矩阵快速幂

题目传送门

题目描述：给出n,x,mod。求s[n].

s[n]=s[n-1]+(x^n)*(n^x)%mod;  

思路：这道题是hdu5950的进阶版。大家可以看这篇博客hdu5950题解。

由于n很大，所以肯定是矩阵快速幂的题目，但是矩阵快速幂只能解决线性的问题，n^4在这个式子中是非线性的，后一项和前一项没有什么直接关系，这里要做一个转换，把n^4变成一个线性的，也就是和（n-1）^4有关系的东西，而这个办法就是：

n^4=(n-1+1)^4=(n-1)^4+4*(n-1)^3+6*(n-1)^2+4*(n-1)^1+(n-1)^0;

而x^n是一个线性的东西，只需要在构造A矩阵的时候在矩阵中多乘以一个x就可以了。

但这道题卡住我的地方是，里面需要算组合数，我之前算组合数的方法是用逆元来求，但是逆元只能处理mod为质数的情况，而这道题mod不是质数，所以不可以这样做（题目还算良心，样例给出的就是合数，否则估计wa死），而要用

c[i][j]=c[i-1][j-1]+c[i-1][j]%mod, 来递推，也就是这样。

inline void init() {
	cc[0][0]=cc[1][0]=cc[1][1]=1;
	for(int i=2;i<=50;i++){
		cc[i][0]=cc[i][i]=1;
		for(int j=1;j<i;j++){
			cc[i][j]=cc[i-1][j]+cc[i-1][j-1]%mod;
		}
	}
}

而这个矩阵是怎样的呢

完整代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#define CLR(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
inline int rd(void) {
	int x=0;int f=1;
	char s=getchar();
	while(s<'0'||s>'9') {	if(s=='-')f=-1;	s=getchar();}
	while(s>='0'&&s<='9') {	x=x*10+s-'0';	s=getchar();}
	x*=f;return x;}
ll n,x,mod;
ll cc[55][55];
inline void init() {
	cc[0][0]=cc[1][0]=cc[1][1]=1;
	for(int i=2; i<=50; i++) {
		cc[i][0]=cc[i][i]=1;
		for(int j=1; j<i; j++) {
			cc[i][j]=cc[i-1][j]+cc[i-1][j-1]%mod;
		}
	}
}
ll f[55],a[55][55];
void mul(ll f[55],ll a[55][55],ll n) {
	ll c[55];
	CLR(c,0);
	for(int j=0; j<n; j++) {
		for(int k=0; k<n; k++) {
			c[j]=(c[j]+f[k]*a[k][j]%mod)%mod;
		}
	}
	memcpy(f,c,sizeof(c));
}
void mulself(ll a[55][55],ll n) {
	ll c[55][55];
	CLR(c,0);
	for(int i=0; i<n; i++) {
		for(int j=0; j<n; j++) {
			for(int k=0; k<n; k++) {
				c[i][j]=(c[i][j]+a[i][k]*a[k][j]%mod)%mod;
			}
		}
	}
	memcpy(a,c,sizeof(c));
}
int main() {
	while(scanf("%lld%lld%lld",&n,&x,&mod)) {
		if(n==-1)break;
		if(n==1) {
			printf("%lld
",x);
		} else {
			init();
			CLR(f,0),CLR(a,0);
			f[0]=x;
			for(int i=1; i<=x+1; i++) {
				f[i]=((ll)pow(2,x-i+1))%mod*x%mod*x%mod;

			}
			a[0][0]=1,a[1][0]=1;
			for(int j=1; j<=x+1; j++) {
				for(int i=j; i<=x+1; i++) {
					a[i][j]=x*cc[x+1-j][i-j]%mod;
				}
			}
			n--;
			for(; n; n>>=1) {
				if(n&1)mul(f,a,x+2);
				mulself(a,x+2);
			}
			printf("%lld
",f[0]);

		}
	}
}

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1244    Accepted Submission(s): 608

 

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

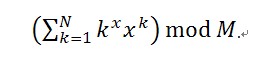
Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*109, and 1 ≤ x ≤ 50.
The input ends up with three negative numbers, which should not be processed as a case.

 

Output

For each test case, print a line with an integer indicating the result.

 

Sample Input

100 1 10000 3 4 1000 -1 -1 -1

 

Sample Output

5050 444